Đề kiểm tra 1 tiết chương 4: Số phức - Đề số 2
-
Hocon247
-
25 câu hỏi
-
45 phút
-
668 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Giả sử ${z_1};{z_2}$ là hai nghiệm phức của phương trình: ${z^2} - 2z + 5 = 0$ và $A,B$ là các điểm biểu diễn của ${z_1};{z_2}$. Tọa độ trung điểm của đoạn thẳng $AB$ là
Phương trình: ${z^2}-2z + 5 = 0$
Có: $\Delta ' = 1 - 5 = - 4 = 4{i^2}$
$ \Rightarrow \sqrt {\Delta '} = \sqrt {4{i^2}} = 2i$
\( \Rightarrow \) Phương trình có $2$ nghiệm là: ${z_1} = 1 + 2i;{z_2} = 1 - 2i$
Khi đó: $A\left( {1;2} \right),B(1; - 2)$
Tọa độ trung điểm đoạn thẳng $AB$ là: $\left( {1;0} \right)$
Hướng dẫn giải:
- Giải phương trình bậc hai tìm hai nghiệm \({z_1},{z_2}\).
- Số phức \(z = a + bi\) có điểm biểu diễn trên mặt phẳng phức là \(M\left( {a;b} \right)\).
- Tọa độ trung điểm \(I\) của đoạn thẳng \(AB\) là \(\left( {\dfrac{{{x_A} + {x_B}}}{2};\dfrac{{{y_A} + {y_B}}}{2}} \right)\)
Cho số phức $z = 2 + 5i$. Tìm số phức \(w = iz + \overline z \).
$\overline z = 2 - 5i \Rightarrow w = i\left( {2 + 5i} \right) + 2 - 5i = - 3 - 3i$.
Hướng dẫn giải:
- Tìm số phức \(\overline z = a - bi\).
- Thay \(z,\overline z \) vào \(w\), sử dụng các công thức cộng và nhân số phức để tìm \(w\).
Giải thích thêm:
Một số em sẽ giải như sau $\bar z = 2 - 5i \Rightarrow w = i\left( {2 + 5i} \right) + 2 - 5i = 2i + 5{i^2} + 2 - 5i = 7 - 3i$ và chọn nhầm đáp án A là sai vì \({i^2} = - 1\) chứ không phải \({i^2} = 1\).
Gọi \({z_1}\) và \({z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 10 = 0\). Tính giá trị biểu thức \(P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}.\)
Ta có \({z^2} + 2z + 10 = 0 \Leftrightarrow {\left( {z + 1} \right)^2} = {\left( {3i} \right)^2} \Leftrightarrow \left[ \begin{array}{l}z = - 1 + 3i = {z_1}\\z = - 1 - 3i = {z_2}\end{array} \right..\)
Suy ra \(P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = {\left( {\sqrt {{{\left( { - 1} \right)}^2} + {3^2}} } \right)^2} + {\left( {\sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2}} } \right)^2} = 10 + 10 = 20\).
Hướng dẫn giải:
- Giải phương trình tìm nghiệm.
- Tính mô đun và thay và biểu thức \(P\).
Kí hiệu \(a\), \(b\) lần lượt là phần thực và phần ảo của số phức \(z = i\left( {1 - i} \right).\) Khẳng định nào sau đây là đúng?
Ta có \(z = i\left( {1 - i} \right) = i - {i^2} = i - \left( { - 1} \right) = 1 + i \Rightarrow \left\{ \begin{array}{l}a = 1\\b = 1\end{array} \right..\)
Hướng dẫn giải:
Biến đổi \(z\) về dạng \(z = a + bi\) suy ra phần thực và phần ảo.
Cho phương trình \(2{z^2} - 3iz + i = 0\). Chọn mệnh đề đúng:
Ta có: \(\Delta = {\left( { - 3i} \right)^2} - 4.2.i = 9{i^2} - 8i = - 9 - 8i\)
Hướng dẫn giải:
Phương trình bậc hai \(A{z^2} + Bz + C = 0\left( {A \ne 0} \right)\) có biệt thức \(\Delta = {B^2} - 4AC\).
Giải thích thêm:
Một số em sẽ tính nhầm \({i^2} = 1\) dẫn đến chọn nhầm đáp án C là sai.
Cho số phức $z$ thỏa mãn $\dfrac{{1 - i}}{{z + 1}} = 1 + i$. Điểm \(M\) biểu diễn của số phức $w = {z^3} + 1$ trên mặt phẳng tọa độ có tọa độ là:
Ta có $\dfrac{{1 - i}}{{z + 1}} = 1 + i \Leftrightarrow z + 1 = \dfrac{{1 - i}}{{1 + i}}$ $ \Leftrightarrow z + 1 = - i \Rightarrow z = - 1 - i$
Suy ra $w = {z^3} + 1 = {\left( { - 1 - i} \right)^3} + 1 = - {\left( {1 + i} \right)^3} + 1 = 3 - 2i$
$ \Rightarrow M\left( {3; - 2} \right)$
Hướng dẫn giải:
- Tính \(z\) suy ra \(w\) và điểm biểu diễn của \(w\).
Gọi \(M\) là điểm biểu diễn của số phức \(z\), biết tập hợp các điểm \(M\) là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng ?
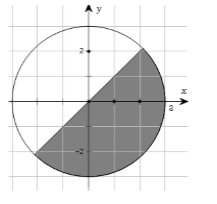
Gọi \(z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)\) và \(M\left( {x;y} \right)\) biểu diễn \(z\) trên mặt phẳng tọa độ.
Phần tô đậm là phần nằm dưới đường thẳng \(y=x\) và trong đường tròn tâm O bán kính 3 nên tọa độ của M thỏa mãn:
\(\left\{ \begin{array}{l}{x^2} + {y^2} \le 9\\y \le x\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\sqrt {{x^2} + {y^2}} \le 3\\y \le x\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left| z \right| \le 3\\y \le x\end{array} \right..\)
Hướng dẫn giải:
- Gọi \(z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)\).
- Tập hợp các điểm bên trong đường tròn tâm O bán kính R là \(x^2+y^2 \le R^2\).
- Tập hợp các điểm bên dưới đường thẳng \(y=x\) là \(y \le x\).
- Nhận xét mối quan hệ của x và y.
Tìm các giá trị của tham số thực \(x,\,{\rm{ }}y\) để số phức \(z = {\left( {x + iy} \right)^2} - 2\left( {x + iy} \right) + 5\) là số thực.
Ta có \(z = {\left( {x + iy} \right)^2} - 2\left( {x + iy} \right) + 5\)\( = {x^2} + 2ixy - {y^2} - 2x - 2iy + 5\)
\( = \left( {{x^2} - {y^2} - 2x + 5} \right) + 2\left( {xy - y} \right)i.\)
Để \(z\) là số thực \( \Leftrightarrow 2\left( {xy - y} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}y = 0\\x = 1\end{array} \right.\).
Hướng dẫn giải:
Số phức \(z = a + bi\) là số thực nếu \(b = 0\).
Cho \({z_1},{z_2}\) là hai nghiệm của phương trình \({z^2} + 2iz + i = 0\). Chọn mệnh đề đúng:
Ta có: \(\left\{ \begin{array}{l}{z_1} + {z_2} = - \dfrac{B}{A} = \dfrac{{ - 2i}}{1} = - 2i\\{z_1}{z_2} = \dfrac{C}{A} = \dfrac{i}{1} = i\end{array} \right.\)
Vậy \({z_1} + {z_2} = - 2i\).
Hướng dẫn giải:
Sử dụng định lý Vi-et cho phương trình bậc hai: \(\left\{ \begin{array}{l}{z_1} + {z_2} = - \dfrac{B}{A}\\{z_1}{z_2} = \dfrac{C}{A}\end{array} \right.\)
Giải thích thêm:
Một số em chọn nhầm đáp án A vì không nhớ đúng công thức tổng hai nghiệm.
Số phức $z$ thỏa mãn $\left| z \right| + z = 0$. Khi đó:
Đặt $z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} $
Ta có: $\left| z \right| + z = 0 \Leftrightarrow \sqrt {{a^2} + {b^2}} + a + bi = 0 + 0i$
$ \Rightarrow \left\{ \begin{array}{l}b = 0\\\sqrt {{a^2} + {b^2}} + a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 0\\\left| a \right| + a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 0\\a \le 0\end{array} \right.$
Hướng dẫn giải:
Đặt $z = a + bi$ , tính $\left| z \right|$ sau đó thay vào phương trình $\left| z \right| + z = 0$. Từ đó tìm được $a$ và $b$
Cho số phức $z = 3 + 2i.$ Tìm phần thực và phần ảo của số phức $\bar z.$
Từ $z = 3 + 2i$, suy ra $\bar z = 3 - 2i$.
Vậy phần thực bằng \(3\) và phần ảo bằng \( - 2\).
Hướng dẫn giải:
Số phức liên hợp của số phức \(z = a + bi\) là \(\overline z = a - bi\).
Cho số phức $z = 1 + \sqrt {3}i $. Khi đó
Ta có: $z = 1 + \sqrt 3 i \Rightarrow \dfrac{1}{z} = \dfrac{1}{{1 + \sqrt 3 i}} = \dfrac{{1 - \sqrt 3 i}}{{(1 - \sqrt 3 i)(1 + \sqrt 3 i)}} $
$= \dfrac{{1 - \sqrt 3 i}}{{{1^2} - {{(\sqrt 3 i)}^2}}} = \dfrac{{1 - \sqrt 3 i}}{4} = \dfrac{1}{4} - \dfrac{{\sqrt 3 }}{4}i$
Hướng dẫn giải:
Cho số phức $ z = a + bi\Rightarrow \dfrac{1}{z} = \dfrac{1}{{a + bi}} = \dfrac{{a - bi}}{{(a - bi)(a + bi)}} = \dfrac{{a - bi}}{{{a^2} - {{(bi)}^2}}} = \dfrac{{a - bi}}{{{a^2} + {b^2}}}$
Giải thích thêm:
Một số em thường nhầm khi tính toán $1^2-(\sqrt{3}i)^2=1-3=-2$ là sai.
Trong $C$, cho phương trình $a{z^2} + bz + c = 0(a \ne 0)(*),a,b,c\in R$. Gọi $\Delta = {b^2} - 4ac$, ta xét các mệnh đề sau:
1) Nếu \(\Delta \) là số thực âm thì phương trình (*) vô nghiệm
2) Nếu \(\Delta \ne 0\) thì phương trình (*) có $2$ nghiệm phân biệt
3) Nếu \(\Delta = 0\) thì phương trình (*) có nghiệm kép
Trong các mệnh đề trên
1) Sai vì nếu \(\Delta < 0\) thì phương trình có $2$ nghiệm phức
2) Đúng
3) Đúng
Vậy có $2$ mệnh đề đúng
Hướng dẫn giải:
Phương pháp giải phương trình bậc hai trên tập số phức: $a{x^2} + bx + c = 0\left( {a \ne 0,a,b,c \in R} \right)$
- Tính \(\Delta = {b^2} - 4ac\).
+ \(\Delta > 0\) thì phương trình có hai nghiệm thực phân biệt \({x_{1,2}} = \dfrac{{ - b \pm \sqrt \Delta }}{{2a}}\).
+ \(\Delta = 0\) thì phương trình có nghiệm kép \({x_{1,2}} = - \dfrac{b}{{2a}}\).
+ \(\Delta < 0\) thì phương trình có hai nghiệm phức phân biệt \({x_{1,2}} = \dfrac{{ - b \pm i\sqrt { - \Delta } }}{{2a}}\).
Giải thích thêm:
Một số em có thể sẽ không phân biệt được sự khác nhau giữa cách giải phương trình bậc hai trên tập số phức với tập số thực dẫn đến chọn nhầm đáp án.
Cho ba điểm \(A,{\rm{ }}B,{\rm{ }}C\) lần lượt biểu diễn ba số phức \({z_1},{\rm{ }}{z_2},{\rm{ }}{z_3}\) với \({z_3} \ne {z_1}\) và \({z_3} \ne {z_2}.\) Biết \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right|\) và \({z_1} + {z_2} = 0.\) Mệnh đề nào sau đây là đúng?
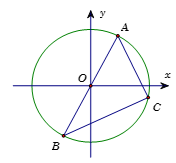
Giả sử \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = R.\)
Khi đó \(A,{\rm{ }}B,{\rm{ }}C\) nằm trên đường tròn \(\left( {O;R} \right)\).
Do \({z_1} + {z_2} = 0\) nên hai điểm \(A,{\rm{ }}B\) đối xứng nhau qua \(O.\) Như vậy điểm \(C\) nằm trên đường tròn đường kính \(AB\) (bỏ đi hai điểm \(A\) và \(B\)) hay tam giác \(ABC\) vuông tại \(C\).
Hướng dẫn giải:
Biểu diễn hình học các điểm biểu diễn \({z_1},{z_2},{z_3}\) và nhận xét tam giác \(ABC\).
Tìm số phức có phần thực bằng $12$ và mô đun bằng $13$:
Ta có: \({\left| z \right|^2} = {a^2} + {b^2} \Leftrightarrow {b^2} = {\left| z \right|^2} - {a^2} \Leftrightarrow b = \pm \sqrt {{{\left| z \right|}^2} - {a^2}} \)
Vậy phần ảo của số phức đó là $ b=\pm \sqrt {{{13}^2} - {{12}^2}} = \pm 5$.
Hướng dẫn giải:
Mô đun số phức \(z = a + bi\) là \(\left| z \right| = \sqrt {{a^2} + {b^2}} \)
Giải thích thêm:
Một số em chỉ tính \(\sqrt {{{13}^2} - {{12}^2}} = 5\) và chọn đáp án B là sai.
Thu gọn số phức $w = {i^5} + {i^6} + {i^7} + ... + {i^{18}}$ có dạng \(a + bi\). Tính tổng \(S = a + b.\)
Ta có $w = {i^5}\left( {1 + i + {i^2} + {i^3} + ... + {i^{13}}} \right) $ $= i.\left( {1 + i + {i^2} + {i^3} + ... + {i^{13}}} \right).$
Dễ thấy $T = 1 + i + {i^2} + {i^3} + ... + {i^{13}}$ là tổng của cấp số nhân có $14$ số hạng, trong đó số hạng đầu tiên ${u_1} = 1$, công bội $q = i$.
Do đó $T = {u_1}\dfrac{{1 - {q^{14}}}}{{1 - q}} = 1.\dfrac{{1 - {i^{14}}}}{{1 - i}} = \dfrac{{1 + 1}}{{1 - i}}$ $ = \dfrac{{2\left( {1 + i} \right)}}{{1 + 1}} = 1 + i$
Vậy \(w = i\left( {1 + i} \right) = - 1 + i \Rightarrow \left\{ \begin{array}{l}a = - 1\\b = 1\end{array} \right.\) \( \Rightarrow S = a + b = 0\)
Hướng dẫn giải:
Sử dụng công thức tính tổng \(n\) số hạng đầu của cấp số nhân \({S_n} = u_1.\dfrac{{1 - {q^n}}}{{1 - q}}\).
Tính môđun của số phức $z$ biết $\overline z = \left( {4 - 3i} \right)\left( {1 + i} \right)$.
Ta có: $\overline z = \left( {4 - 3i} \right)\left( {1 + i} \right) = 7 + i \Rightarrow z = 7 - i \Rightarrow \left| z \right| = \sqrt {50} = 5\sqrt 2 $
Hướng dẫn giải:
Áp dụng công thức $z = a + bi \Rightarrow \overline z = a - bi;\left| z \right| = \left| {\overline z } \right| = \sqrt {{a^2} + {b^2}} $
Giải thích thêm:
Có thể áp dụng các chú ý về mô đun số phức như sau: \(\left| {z.z'} \right| = \left| z \right|.\left| {z'} \right|\) và \(\left| z \right| = \left| {\overline z } \right|\):
Ta có: \(\left| z \right| = \left| {\overline z } \right| = \left| {\left( {4 - 3i} \right)\left( {1 + i} \right)} \right| = \left| {4 + 3i} \right|\left| {1 + i} \right| = \sqrt {{4^2} + {3^2}} .\sqrt {{1^2} + {1^2}} = 5\sqrt 2 \)
Kí hiệu \({z_1},{\rm{ }}{z_2},\,{\rm{ }}{z_3}\) và \({z_4}\) là bốn nghiệm phức của phương trình $6{z^4} + 19{z^2} + 15 = 0.$ Tính tổng \(T = \dfrac{1}{{{z_1}}} + \dfrac{1}{{{z_2}}} + \dfrac{1}{{{z_3}}} + \dfrac{1}{{{z_4}}}.\)
Phương trình $6{z^4} + 19{z^2} + 15 = 0$ $ \Leftrightarrow \left( {2{z^2} + 3} \right)\left( {3{z^2} + 5} \right) = 0$ $ \Leftrightarrow \left[ \begin{array}{l}2{z^2} = - \,3\\3{z^2} = - \,5\end{array} \right.$
$ \Leftrightarrow \left[ \begin{array}{l}{z^2} = - \dfrac{3}{2}\\{z^2} = - \dfrac{5}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{z^2} = \dfrac{{3{i^2}}}{2}\\{z^2} = \dfrac{{5{i^2}}}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = \pm \,\dfrac{{i\sqrt 6 }}{2}\\z = \pm \,\dfrac{{i\sqrt {15} }}{3}\end{array} \right.$ $ \Rightarrow T = \dfrac{2}{{i\sqrt 6 }} - \dfrac{2}{{i\sqrt 6 }} + \dfrac{3}{{i\sqrt {15} }} - \dfrac{3}{{i\sqrt {15} }} = 0$
Hướng dẫn giải:
- Giải phương trình tìm các nghiệm \({z_1},{z_2},{z_3},{z_4}\).
- Thay vào tính giá trị biểu thức và kết luận.
Cho số phức \({\rm{w}}\)và hai số thực \(a,b\). Biết \({z_1} = {\rm{w}} + 2i\) và \({z_2} = 2w - 3\) là 2 nghiệm phức của phương trình \({z^2} + az + b = 0\). Tính \(T = \left| {{z_1}} \right| + \left| {{z_2}} \right|\).
Đặt \({\rm{w}} = x + yi\). Khi đó:
\(\begin{array}{l}{z_1} = x + yi + 2i = x + \left( {y + 2} \right)i;{z_2} = 2(x + yi) - 3 = \left( {2x - 3} \right) + 2yi \\ \Rightarrow {z_2} = \left( {2x - 3} \right) - 2yi\\{z_1} = \overline {{z_2}} \Leftrightarrow \left\{ \begin{array}{l}x = 2x - 3\\y + 2 = - 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - \dfrac{2}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{z_1} = 3 + \dfrac{4}{3}i\\{z_2} = 3 - \dfrac{4}{3}i\end{array} \right. \\ \Rightarrow T = \left| {{z_1}} \right| + \left| {{z_2}} \right| = \sqrt {{3^2} + {{\left( {\dfrac{4}{3}} \right)}^2}} + \sqrt {{3^2} + {{\left( { - \dfrac{4}{3}} \right)}^2}} = \dfrac{{2\sqrt {97} }}{3}\end{array}\)
Hướng dẫn giải:
Nếu \({z_1};{z_2}\) là hai nghiệm phức của phương trình \({z^2} + az + b = 0\) thì \({z_1} = \overline {{z_2}} \).
Gọi ${z_1}$, ${z_2}$ là hai nghiệm phức của phương trình ${z^2} - 2z + 2 = 0$. Tính giá trị biểu thức $P = z_1^{2016} + z_2^{2016}.$
Biệt số $\Delta = 4 - 8 = - 4 = {\left( {2i} \right)^2}$.
Do đó phương trình có hai nghiệm phức: ${z_1} = \dfrac{{2 - 2i}}{2} = 1 - i$ và ${z_2} = \dfrac{{2 + 2i}}{2} = 1 + i$.
Suy ra $z_1^{2016} = {\left( {1 - i} \right)^{2016}} = {\left[ {{{\left( {1 - i} \right)}^2}} \right]^{1008}} = {\left( { - 2i} \right)^{1008}} = {\left( { - 2} \right)^{1008}}.{i^{1008}} = {2^{1008}}.1 = {2^{1008}}$;
$z_2^{2016} = {\left( {1 + i} \right)^{2016}} = {\left[ {{{\left( {1 + i} \right)}^2}} \right]^{1008}} = {\left( {2i} \right)^{1008}} = {2^{1008}}.{i^{1008}} = {2^{1008}}.1 = {2^{1008}}$.
Vậy $P = z_1^{2016} + z_2^{2016} = {2^{1008}} + {2^{1008}} = {2^{1009}}$.
Hướng dẫn giải:
- Giải phương trình tìm nghiệm.
- Thay vào tính giá trị biểu thức.
Tập điểm biểu diễn số phức $z$ thỏa mãn ${\left| z \right|^2} = {z^2}$ là:
Đặt $z = x + yi{\rm{ }}\left( {x,y \in R} \right)$ thì ${\left| z \right|^2} = {z^2} \Leftrightarrow {x^2} + {y^2} = {x^2} + 2xyi - {y^2} \Leftrightarrow \left\{ \begin{array}{l}xy = 0\\{x^2} + {y^2} = {x^2} - {y^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \in R\\y = 0\end{array} \right.$
Do đó tập điểm biểu diễn $z$ là đường thẳng $y = 0$.
Hướng dẫn giải:
Bước 1: Gọi số phức \(z = x + yi\left( {x,y \in R} \right)\) có điểm biểu diễn là \(M\left( {x;y} \right)\).
Bước 2: Thay \(z = x + yi\) vào điều kiện đã cho dẫn đến phương trình liên hệ giữa \(x,y\).
Bước 3: Kết luận:
- Phương trình đường thẳng: \(Ax + By + C = 0\)
- Phương trình đường tròn: \({x^2} + {y^2} - 2ax - 2by + c = 0\)
- Phương trình parabol: \(y = a{x^2} + bx + c\) hoặc \(x = a{y^2} + by + c\)
- Phương trình elip: \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\)
Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức $z$ thỏa mãn điều kiện \(2|z - 1 - 2i| = |3i + 1 - 2\bar z|\).
Giả sử ta có số phức $z = x + yi$. Thay vào điều kiện \(2|z - 1 - 2i| = |3i + 1 - 2\bar z|\) có
\(2|(x + yi) - 1 - 2i| = |3i + 1 - 2(x - yi)| \Leftrightarrow 2|(x - 1) + (y - 2)i| = |(1 - 2x) + (3 + 2y)i|\) \( \Leftrightarrow 2\sqrt {{{(x - 1)}^2} + {{(y - 2)}^2}} = \sqrt {{{(1 - 2x)}^2} + {{(3 + 2y)}^2}} \)
\( \Leftrightarrow 4{(x - 1)^2} + 4{(y - 2)^2} = {(1 - 2x)^2} + {(3 + 2y)^2}\)
\( \Leftrightarrow 4{x^2} - 8x + 4 + 4{y^2} - 16y + 16 = 4{x^2} - 4x + 1 + 4{y^2} + 12y + 9\)
\( \Leftrightarrow 4x + 28y - 10 = 0\)
\( \Leftrightarrow 2x + 14y - 5 = 0\)
Hướng dẫn giải:
Phương pháp tìm tập hợp điểm biểu diễn số phức
Bước 1: Gọi số phức \(z = x + yi\) có điểm biểu diễn là \(M(x;y)\)
Bước 2: Thay \(z\) vào đề bài \( \Rightarrow \) Sinh ra một phương trình:
+) Đường thẳng: \(Ax + By + C = 0.\)
+) Đường tròn: \({x^2} + {y^2} - 2ax - 2by + c = 0.\)
+) Parabol: \(y = a.{x^2} + bx + c\)
+) Elip: \(\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} = 1\)
Tìm giá trị nhỏ nhất của \(|z|\), biết rằng \(z\) thỏa mãn điều kiện \(|\dfrac{{4 + 2i}}{{1 - i}}z - 1| = 1\).
Có \(\dfrac{{4 + 2i}}{{1 - i}} = 1 + 3i\). Đặt \(z = x + yi\) thì
\(\dfrac{{4 + 2i}}{{1 - i}}z - 1 = (1 + 3i)(x + yi) - 1 = (x - 3y - 1) + (3x + y)i\)
Điều kiện đã cho trong bài được viết lại thành
\({(x - 3y - 1)^2} + {(3x + y)^2} = 1\)
\( \Leftrightarrow {(x - 3y)^2} - 2(x - 3y) + 1 + {(3x + y)^2} = 1\)
\( \Leftrightarrow 10{x^2} + 10{y^2} - 2x + 6y = 0\)
\( \Leftrightarrow \left( {{x^2} - \dfrac{1}{5}x} \right) + \left( {{y^2} + \dfrac{3}{5}y} \right) = 0\)
\( \Leftrightarrow {\left( {x - \dfrac{1}{{10}}} \right)^2} + {\left( {y + \dfrac{3}{{10}}} \right)^2} = \dfrac{1}{{10}}\) (*)
Điểm biểu diễn \(M(x,y)\) của \(z\) chạy trên đường tròn (*). Cần tìm điểm \(M(x,y)\) thuộc đường tròn này để $OM$ nhỏ nhất.
Vì đường tròn này qua $O$ nên min $OM = 0$ khi \(M \equiv O\) hay $M\left( {0,0} \right)$, do đó $z = 0$ hay $min\left| z \right| = 0$.
Hướng dẫn giải:
Gọi \(z = x + yi\), thay vào điều kiện đề bài tìm mối liên hệ \(x,y\).
Áp dụng phương pháp hình học để tìm điều kiện cho \(\left| z \right|\) đạt GTNN.
Giải thích thêm:
- Xác định sai mô đun các số phức.
- Tìm sai mối liên hệ \(x,y\).
- Không đưa được bài toán từ dạng đại số về hình học.
Trong các số phức z thỏa mãn \(\left| {z + 3 + 4i} \right| = 2\) , gọi \({z_0}\) là số phức có mô đun nhỏ nhất. Khi đó:
Giả sử $z = a + bi\left( {a,b \in R} \right)$ ta có:
$\left| {z + 3 + 4i} \right| = 2 \Leftrightarrow \left| {(a + 3) + (b + 4)i} \right| = 2 \Leftrightarrow {(a + 3)^2} + {(b + 4)^2} = 4$
Do đó tập hợp điểm biểu diễn số phức $z$ thuộc đường tròn tâm $I\left( { - 3; - 4} \right)$ và bán kính $r = 2$
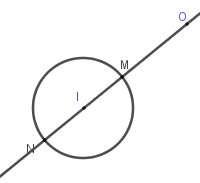
Từ hình vẽ ta thấy số phức \({z_0}\) có mô đun nhỏ nhất nếu \({z_0}\) có điểm biểu diễn là \(M\).
Ta có: $\overrightarrow {OI} = ( - 3; - 4)$ nên đường thẳng đi qua \(O\) và \(I\) là $OI:\left\{ \begin{array}{l}x = 3t\\y = 4t\end{array} \right. \Rightarrow M\left( {3t;4t} \right)$
Mặt khác $M \in \left( C \right)$ nên: ${\left( {3t + 3} \right)^2} + {\left( {4t + 4} \right)^2} = 4 \Leftrightarrow 25{t^2} + 50t + 21 = 0 \Leftrightarrow \left\{ \begin{array}{l}t = \dfrac{{ - 3}}{5}\\t = \dfrac{{ - 7}}{5}\end{array} \right.$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ hoặc $M\left( {\dfrac{{ - 21}}{5};\dfrac{{ - 28}}{5}} \right)$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ thuộc $\left( C \right)$ và gần $O$ nhất.
$ \Rightarrow z = \dfrac{{ - 9}}{5} - \dfrac{{12}}{5}i \Rightarrow \left| z \right| = 3$
Hướng dẫn giải:
- Bước 1: Gọi số phức \(z = x + yi\left( {x,y \in R} \right)\)
- Bước 2: Thay \(z\) và biểu thức đã cho tìm mối quan hệ của \(x,y\) suy ra tập hợp biểu diễn của số phức \(z\).
- Bước 3: Sử dụng mối quan hệ hình học để tìm mô đun số phức cần tìm.
Xét số phức \(z\) thỏa mãn \(\left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right| = 6\sqrt 2 \). Gọi \(m,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \(\left| {z - 1 + i} \right|\). Tính \(P = m + M\).
Gọi $z=x+yi\left( x,y\in R \right)$
Trên mặt phẳng tọa độ $Oxy$ gọi $P\left( {x;y} \right)$ là điểm biểu diễn của số phức $z$
Gọi $A\left( {-2;1} \right),B\left( {4;7} \right)$ thì
$\begin{array}{l}AB = 6\sqrt 2 = \left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right|\\ = \sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y - 1} \right)}^2}} + \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 7} \right)}^2}} = PA + PB\end{array}$
Suy ra tập hợp các điểm $P$ thỏa mãn chính là đoạn thẳng AB
Có $\left| {z - 1 + i} \right| = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} = PC$ với $C\left( {1;-1} \right)$
Do đó \(P{C_{\min }}\) khi \(P\) là hình chiếu của \(C\) lên \(AB\) và \(P{C_{\max }}\) khi \(P \equiv B\)
Suy ra $M = CB = \sqrt {73} $.
Ta có: \(AB:\dfrac{{x + 2}}{{4 + 2}} = \dfrac{{y - 1}}{{7 - 1}} \Leftrightarrow x - y + 3 = 0\)\( \Rightarrow m=d\left( {C,AB} \right) = \dfrac{{\left| {1 - \left( { - 1} \right) + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{5}{{\sqrt 2 }}\)
$\Rightarrow M + m = \dfrac{{5\sqrt 2 + 2\sqrt {73} }}{2}$
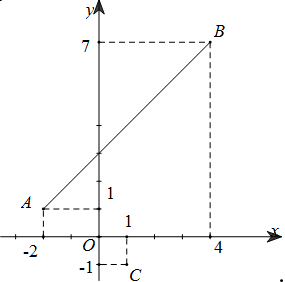
Hướng dẫn giải:
- Gọi $z = x + yi$ và tìm tập hợp điểm biểu diễn số phức $z$ thỏa mãn bài toán.
- Biểu diễn tập hợp điểm đó trên hệ trục tọa độ từ đó tìm GTLN, GTNN của biểu thức đã cho.
Đề thi liên quan
-
Đề kiểm tra 15 phút chương 4: Số phức - Đề số 1
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 4: Số phức - Đề số 2
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 4: Số phức - Đề số 3
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 4: Số phức - Đề số 1
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 4: Số phức - Đề số 3
-
25 câu hỏi
-
45 phút
-

