Trong $C$, cho phương trình $a{z^2} + bz + c = 0(a \ne 0)(*),a,b,c\in R$. Gọi $\Delta = {b^2} - 4ac$, ta xét các mệnh đề sau:
1) Nếu \(\Delta \) là số thực âm thì phương trình (*) vô nghiệm
2) Nếu \(\Delta \ne 0\) thì phương trình (*) có $2$ nghiệm phân biệt
3) Nếu \(\Delta = 0\) thì phương trình (*) có nghiệm kép
Trong các mệnh đề trên
A.
Không có mệnh đề nào đúng
B.
Có $1$ mệnh đề đúng
C.
Có $2$ mệnh đề đúng
D.
Cả $3$ mệnh đề đều đúng
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
1) Sai vì nếu \(\Delta < 0\) thì phương trình có $2$ nghiệm phức
2) Đúng
3) Đúng
Vậy có $2$ mệnh đề đúng
Hướng dẫn giải:
Phương pháp giải phương trình bậc hai trên tập số phức: $a{x^2} + bx + c = 0\left( {a \ne 0,a,b,c \in R} \right)$
- Tính \(\Delta = {b^2} - 4ac\).
+ \(\Delta > 0\) thì phương trình có hai nghiệm thực phân biệt \({x_{1,2}} = \dfrac{{ - b \pm \sqrt \Delta }}{{2a}}\).
+ \(\Delta = 0\) thì phương trình có nghiệm kép \({x_{1,2}} = - \dfrac{b}{{2a}}\).
+ \(\Delta < 0\) thì phương trình có hai nghiệm phức phân biệt \({x_{1,2}} = \dfrac{{ - b \pm i\sqrt { - \Delta } }}{{2a}}\).
Giải thích thêm:
Một số em có thể sẽ không phân biệt được sự khác nhau giữa cách giải phương trình bậc hai trên tập số phức với tập số thực dẫn đến chọn nhầm đáp án.
1) Sai vì nếu \(\Delta < 0\) thì phương trình có $2$ nghiệm phức
2) Đúng
3) Đúng
Vậy có $2$ mệnh đề đúng
Hướng dẫn giải:
Phương pháp giải phương trình bậc hai trên tập số phức: $a{x^2} + bx + c = 0\left( {a \ne 0,a,b,c \in R} \right)$
- Tính \(\Delta = {b^2} - 4ac\).
+ \(\Delta > 0\) thì phương trình có hai nghiệm thực phân biệt \({x_{1,2}} = \dfrac{{ - b \pm \sqrt \Delta }}{{2a}}\).
+ \(\Delta = 0\) thì phương trình có nghiệm kép \({x_{1,2}} = - \dfrac{b}{{2a}}\).
+ \(\Delta < 0\) thì phương trình có hai nghiệm phức phân biệt \({x_{1,2}} = \dfrac{{ - b \pm i\sqrt { - \Delta } }}{{2a}}\).
Giải thích thêm:
Một số em có thể sẽ không phân biệt được sự khác nhau giữa cách giải phương trình bậc hai trên tập số phức với tập số thực dẫn đến chọn nhầm đáp án.
CÂU HỎI CÙNG CHỦ ĐỀ
Giả sử ${z_1};{z_2}$ là hai nghiệm phức của phương trình: ${z^2} - 2z + 5 = 0$ và $A,B$ là các điểm biểu diễn của ${z_1};{z_2}$. Tọa độ trung điểm của đoạn thẳng $AB$ là
Kí hiệu \({z_1},{\rm{ }}{z_2},\,{\rm{ }}{z_3}\) và \({z_4}\) là bốn nghiệm phức của phương trình $6{z^4} + 19{z^2} + 15 = 0.$ Tính tổng \(T = \dfrac{1}{{{z_1}}} + \dfrac{1}{{{z_2}}} + \dfrac{1}{{{z_3}}} + \dfrac{1}{{{z_4}}}.\)
Cho số phức $z = 2 + 5i$. Tìm số phức \(w = iz + \overline z \).
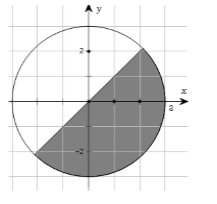
Gọi \(M\) là điểm biểu diễn của số phức \(z\), biết tập hợp các điểm \(M\) là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng ?
Cho số phức $z = 3 + 2i.$ Tìm phần thực và phần ảo của số phức $\bar z.$
Tìm số phức có phần thực bằng $12$ và mô đun bằng $13$:
Tập điểm biểu diễn số phức $z$ thỏa mãn ${\left| z \right|^2} = {z^2}$ là:
Gọi ${z_1}$, ${z_2}$ là hai nghiệm phức của phương trình ${z^2} - 2z + 2 = 0$. Tính giá trị biểu thức $P = z_1^{2016} + z_2^{2016}.$
Tính môđun của số phức $z$ biết $\overline z = \left( {4 - 3i} \right)\left( {1 + i} \right)$.
Tìm các giá trị của tham số thực \(x,\,{\rm{ }}y\) để số phức \(z = {\left( {x + iy} \right)^2} - 2\left( {x + iy} \right) + 5\) là số thực.
Thu gọn số phức $w = {i^5} + {i^6} + {i^7} + ... + {i^{18}}$ có dạng \(a + bi\). Tính tổng \(S = a + b.\)
Trong các số phức z thỏa mãn \(\left| {z + 3 + 4i} \right| = 2\) , gọi \({z_0}\) là số phức có mô đun nhỏ nhất. Khi đó:
Cho phương trình \(2{z^2} - 3iz + i = 0\). Chọn mệnh đề đúng:
Kí hiệu \(a\), \(b\) lần lượt là phần thực và phần ảo của số phức \(z = i\left( {1 - i} \right).\) Khẳng định nào sau đây là đúng?

