Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
Ta có $w = {i^5}\left( {1 + i + {i^2} + {i^3} + ... + {i^{13}}} \right) $ $= i.\left( {1 + i + {i^2} + {i^3} + ... + {i^{13}}} \right).$
Dễ thấy $T = 1 + i + {i^2} + {i^3} + ... + {i^{13}}$ là tổng của cấp số nhân có $14$ số hạng, trong đó số hạng đầu tiên ${u_1} = 1$, công bội $q = i$.
Do đó $T = {u_1}\dfrac{{1 - {q^{14}}}}{{1 - q}} = 1.\dfrac{{1 - {i^{14}}}}{{1 - i}} = \dfrac{{1 + 1}}{{1 - i}}$ $ = \dfrac{{2\left( {1 + i} \right)}}{{1 + 1}} = 1 + i$
Vậy \(w = i\left( {1 + i} \right) = - 1 + i \Rightarrow \left\{ \begin{array}{l}a = - 1\\b = 1\end{array} \right.\) \( \Rightarrow S = a + b = 0\)
Hướng dẫn giải:
Sử dụng công thức tính tổng \(n\) số hạng đầu của cấp số nhân \({S_n} = u_1.\dfrac{{1 - {q^n}}}{{1 - q}}\).
Ta có $w = {i^5}\left( {1 + i + {i^2} + {i^3} + ... + {i^{13}}} \right) $ $= i.\left( {1 + i + {i^2} + {i^3} + ... + {i^{13}}} \right).$
Dễ thấy $T = 1 + i + {i^2} + {i^3} + ... + {i^{13}}$ là tổng của cấp số nhân có $14$ số hạng, trong đó số hạng đầu tiên ${u_1} = 1$, công bội $q = i$.
Do đó $T = {u_1}\dfrac{{1 - {q^{14}}}}{{1 - q}} = 1.\dfrac{{1 - {i^{14}}}}{{1 - i}} = \dfrac{{1 + 1}}{{1 - i}}$ $ = \dfrac{{2\left( {1 + i} \right)}}{{1 + 1}} = 1 + i$
Vậy \(w = i\left( {1 + i} \right) = - 1 + i \Rightarrow \left\{ \begin{array}{l}a = - 1\\b = 1\end{array} \right.\) \( \Rightarrow S = a + b = 0\)
Hướng dẫn giải:
Sử dụng công thức tính tổng \(n\) số hạng đầu của cấp số nhân \({S_n} = u_1.\dfrac{{1 - {q^n}}}{{1 - q}}\).
CÂU HỎI CÙNG CHỦ ĐỀ
Giả sử ${z_1};{z_2}$ là hai nghiệm phức của phương trình: ${z^2} - 2z + 5 = 0$ và $A,B$ là các điểm biểu diễn của ${z_1};{z_2}$. Tọa độ trung điểm của đoạn thẳng $AB$ là
Kí hiệu \({z_1},{\rm{ }}{z_2},\,{\rm{ }}{z_3}\) và \({z_4}\) là bốn nghiệm phức của phương trình $6{z^4} + 19{z^2} + 15 = 0.$ Tính tổng \(T = \dfrac{1}{{{z_1}}} + \dfrac{1}{{{z_2}}} + \dfrac{1}{{{z_3}}} + \dfrac{1}{{{z_4}}}.\)
Cho số phức $z = 2 + 5i$. Tìm số phức \(w = iz + \overline z \).
Tìm số phức có phần thực bằng $12$ và mô đun bằng $13$:
Cho số phức $z = 3 + 2i.$ Tìm phần thực và phần ảo của số phức $\bar z.$
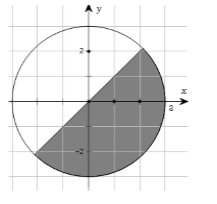
Gọi \(M\) là điểm biểu diễn của số phức \(z\), biết tập hợp các điểm \(M\) là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng ?
Tính môđun của số phức $z$ biết $\overline z = \left( {4 - 3i} \right)\left( {1 + i} \right)$.
Tập điểm biểu diễn số phức $z$ thỏa mãn ${\left| z \right|^2} = {z^2}$ là:
Gọi ${z_1}$, ${z_2}$ là hai nghiệm phức của phương trình ${z^2} - 2z + 2 = 0$. Tính giá trị biểu thức $P = z_1^{2016} + z_2^{2016}.$
Tìm các giá trị của tham số thực \(x,\,{\rm{ }}y\) để số phức \(z = {\left( {x + iy} \right)^2} - 2\left( {x + iy} \right) + 5\) là số thực.
Trong $C$, cho phương trình $a{z^2} + bz + c = 0(a \ne 0)(*),a,b,c\in R$. Gọi $\Delta = {b^2} - 4ac$, ta xét các mệnh đề sau:
1) Nếu \(\Delta \) là số thực âm thì phương trình (*) vô nghiệm
2) Nếu \(\Delta \ne 0\) thì phương trình (*) có $2$ nghiệm phân biệt
3) Nếu \(\Delta = 0\) thì phương trình (*) có nghiệm kép
Trong các mệnh đề trên
Trong các số phức z thỏa mãn \(\left| {z + 3 + 4i} \right| = 2\) , gọi \({z_0}\) là số phức có mô đun nhỏ nhất. Khi đó:
Cho phương trình \(2{z^2} - 3iz + i = 0\). Chọn mệnh đề đúng:
Kí hiệu \(a\), \(b\) lần lượt là phần thực và phần ảo của số phức \(z = i\left( {1 - i} \right).\) Khẳng định nào sau đây là đúng?

