Đề kiểm tra 1 tiết chương 4: Số phức - Đề số 3
-
Hocon247
-
25 câu hỏi
-
45 phút
-
666 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Căn bậc hai của số \(a = - 3\) là:
Căn bậc hai của số \(a = - 3\) là \(i\sqrt 3 \) và \( - i\sqrt 3 \).
Phương trình: ${z^2} + az + b = 0$ \(\left( {a,b \in \mathbb{R}} \right)\) có một nghiệm phức là $z = 1 + 2i$ . Tổng $2$ số $a$ và $b$ bằng
Vì $z = 1 + 2i$ là nghiệm của phương trình nên:
${\left( {1 + 2i} \right)^2} + a\left( {1 + 2i} \right) + b = 0$
$\begin{array}{l} \Leftrightarrow 1 + 4i + 4{i^2} + a + 2ai + b = 0\\ \Leftrightarrow (2a + 4)i + a + b - 3 = 0\end{array}$
$ \Leftrightarrow \left\{ \begin{array}{l}2a + 4 = 0\\a + b - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = 5\end{array} \right.\; \Rightarrow a + b = - 2 + 5 = 3$
Hướng dẫn giải:
Nếu \(z = {z_0}\) là một nghiệm của phương trình \(f\left( z \right) = 0\) thì \(f\left( {{z_0}} \right) = 0\).
Áp dụng phương pháp đồng nhất hệ số để tìm \(a,b\).
Giải thích thêm:
Các em cũng có thể nhận xét: Đối với phương trình bậc hai hệ số thực mà có nghiệm phức thì hai nghiệm đó là hai số phức liên hợp, do đó nếu \(1 + 2i\) là một nghiệm của phương trình thì \(1 - 2i\) cũng là một nghiệm của phương trình.
Từ đó \(\left\{ \begin{array}{l} - a = 1 + 2i + 1 - 2i = 2 \Rightarrow a = - 2\\b = \left( {1 + 2i} \right)\left( {1 - 2i} \right) = 1 - {\left( {2i} \right)^2} = 5\end{array} \right.\)
Chọn mệnh đề đúng:
Ta có \(\left| z \right| = \left| {\overline z } \right|\) nên B đúng.
Giải thích thêm:
Một số em có thể sẽ nghĩ rằng \(\left| z \right| = \sqrt {{a^2} - {b^2}} \) dẫn tới không chọn được đáp án.
Tìm phần ảo \(b\) của số phức $w = \dfrac{1}{{2i}}\left( {z - \bar z} \right)$ với $z = 5 - 3i$.
Ta có $z = 5 - 3i \Rightarrow \bar z = 5 + 3i.$
Vậy $\dfrac{1}{{2i}}\left( {z - \bar z} \right) = \dfrac{1}{{2i}}\left[ {\left( {5 - 3i} \right) - \left( {5 + 3i} \right)} \right] = \dfrac{1}{{2i}}\left( { - 6i} \right) = - 3 = - 3 + 0i.$
Hướng dẫn giải:
Tìm \(\overline z \) và thay và tìm \(w\).
Cho hai số phức ${z_1} = 1 + i$ và ${z_2} = 2 - 3i$. Tính môđun của số phức ${z_1} - {z_2}.$
Ta có ${z_1} - {z_2} = - 1 + 4i \Rightarrow \left| {{z_1} - {z_2}} \right| = \sqrt {17} $.
Hướng dẫn giải:
Tính \({z_1} - {z_2}\) suy ra mô đun.
Nghiệm của phương trình: ${z^2} + (1 - i)z - 18 + 13i = 0$ là:
Phương trình: \({z^2} + (1 - i)z - 18 + 13i = 0\)
Có: \(\Delta = {\left( {1 - i} \right)^2} - 4( - 18 + 13i) = 1 - 2i + {i^2} + 72 - 52i\)
\( = 72 - 54i = 81 - 2.9.3i + 9{i^2} = {\left( {9 - 3i} \right)^2}\)
\( \Rightarrow \delta = 9 - 3i\) là một căn bậc hai của \(\Delta \).
\( \Rightarrow \) Phương trình có \(2\) nghiệm là: \({z_1} = \dfrac{{ - 1 + i + 9 - 3i}}{2} = 4 - i;\) \({z_2} = \dfrac{{ - 1 + i - 9 + 3i}}{2} = - 5 + 2i\)
Hướng dẫn giải:
Phương pháp giải phương trình bậc hai trên tập số phức: \(a{x^2} + bx + c = 0\left( {a \ne 0,a,b,c \in C} \right)\)
- Tính \(\Delta = {b^2} - 4ac\).
- Tìm một căn bậc hai \(\delta \) của \(\Delta \).
- Áp dụng công thức nghiệm \({x_{1,2}} = \dfrac{{ - b \pm \delta }}{{2a}}\).
Giải thích thêm:
Các em thường mắc sai lầm như sau:
- Tính sai \(\Delta \).
- Tìm sai căn bậc hai của \(\Delta \).
- Áp dụng sai công thức nghiệm.
Tập hợp các điểm biểu diễn hình học của số phức $z$ là đường thẳng $\Delta $ như hình vẽ. Tìm giá trị nhỏ nhất của \(\left| z \right|\).
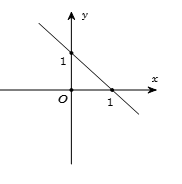
\(\Delta \) đi qua hai điểm \(\left( {1;0} \right)\) và \(\left( {0;1} \right)\) nên có phương trình $\Delta :x + y - 1 = 0$.
Khi đó ${\left| z \right|_{\min }} = d\left[ {O,\Delta } \right] = \dfrac{{\left| { - 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{1}{{\sqrt 2 }}.$
Hướng dẫn giải:
- Viết phương trình \(\Delta \) suy ra khoảng cách theo công thức \(d\left( {A,\Delta } \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Tìm điểm $M$ biểu diễn số phức \(z = i - 2\)
$z = i - 2 = - 2 + i$ nên điểm biểu diễn là $M\left( { - 2;1} \right)$
Hướng dẫn giải:
Điểm biều diễn của số phức $z = a + bi$ là $M\left( {a;b} \right)$
Giải thích thêm:
Một số em sẽ chọn đáp án A vì không đưa số phức \(z\) về dạng \(a + bi\).
Cho số phức $z = 3 + 2i.$ Tìm phần thực và phần ảo của số phức $\bar z.$
Từ $z = 3 + 2i$, suy ra $\bar z = 3 - 2i$.
Vậy phần thực bằng \(3\) và phần ảo bằng \( - 2\).
Hướng dẫn giải:
Số phức liên hợp của số phức \(z = a + bi\) là \(\overline z = a - bi\).
Với hai số phức bất kì ${z_1},{z_2}$ , khẳng định nào sau đây đúng:
Ta có: \(\left| {\left| {{z_1}} \right| - \left| {{z_2}} \right|} \right| \le \left| {{z_1} \pm {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|\) nên A đúng.
Hướng dẫn giải:
Dựa vào tính chất của bất đẳng thức chứa dấu giá trị tuyệt đối:
$\left| {\left| x \right| - \left| y \right|} \right| \le \left| {x + y} \right| \le \left| x \right| + \left| y \right|$
Gọi \(A\) là điểm biểu diễn của số phức \(z = 3 + 2i\) và \(B\) là điểm biểu diễn của số phức \(z' = 2 + 3i\). Mệnh đề nào sau đây là đúng?
Số phức \(z = 3 + 2i\) có điểm biểu diễn là \(A\) suy ra \(A\left( {3;2} \right)\).
Số phức \(z' = 2 + 3i\) có điểm biểu diễn là \(B\) suy ra \(B\left( {2;3} \right)\).
Ta thấy \(\left\{ \begin{array}{l}{x_A} = {y_B}\\{y_A} = {x_B}\end{array} \right.\) nên hai điểm \(A\) và \(B\) đối xứng nhau qua đường thẳng \(y = x\).
Hướng dẫn giải:
Tìm tọa độ mỗi điểm \(A,B\) và nhận xét vị trí của \(A,B\).
Cho số phức $z$ thỏa mãn $\left( {2-i} \right)z = 7-i$ . Hỏi điểm biểu diễn của $z$ là điểm nào trong các điểm $M,N,P,Q$ ở hình dưới.
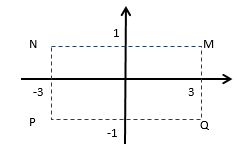
\(\left( {2 - i} \right)z = 7 - i \Rightarrow z = \dfrac{{7 - i}}{{2 - i}} = \dfrac{{(7 - i)(2 + i)}}{5} = \dfrac{{15 + 5i}}{5} = 3 + i\)
Suy ra điểm có tọa độ $\left( {3;1} \right)$ sẽ biểu diễn số phức $z$, suy ra $M$ thỏa mãn.
Hướng dẫn giải:
+ Biến đổi, sử dụng các quy tắc về cộng trừ, nhân chia số phức để tìm ra số phức $z$
+ Nếu $z = a + bi$ thì điểm có tọa độ $\left( {a;b} \right)$ là điểm biểu diễn số phức $z$
Biết rằng có duy nhất một cặp số thực $\left( {x;y} \right)$ thỏa mãn $\left( {x + y} \right) + \left( {x - y} \right)i = 5 + 3i$. Tính \(S = x + y.\)
Ta có $\left( {x + y} \right) + \left( {x - y} \right)i = 5 + 3i \Leftrightarrow \left( {x + y - 5} \right) + \left( {x - y - 3} \right)i = 0 \Leftrightarrow \left\{ \begin{array}{l}x + y - 5 = 0\\x - y - 3 = 0\end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 1\end{array} \right. \Rightarrow S = x + y = 4 + 1 = 5.$
Hướng dẫn giải:
Hai số phức \(z = a + bi\) và \(z' = a' + b'i\) bằng nhau nếu \(a = a',b = b'\)
Cho hai số phức ${z_1} = 3 + 4i,\,\,{z_2} = 4 - 3i$. Mệnh đề nào sau đây là đúng?
Ta có $i.{z_2} = i\left( {4 - 3i} \right) = 4i - 3{i^2} = 3 + 4i = {z_1} \Rightarrow {z_1} = i.{z_2}$.
Hướng dẫn giải:
- Xét tính đúng sai của từng ĐA và kết luận.
Chú ý: Số phức liên hợp của \(z = a + bi\) là \(\overline z = a - bi\).
Gọi \({z_1}\) và \({z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 10 = 0\). Tính giá trị biểu thức \(P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}.\)
Ta có \({z^2} + 2z + 10 = 0 \Leftrightarrow {\left( {z + 1} \right)^2} = {\left( {3i} \right)^2} \Leftrightarrow \left[ \begin{array}{l}z = - 1 + 3i = {z_1}\\z = - 1 - 3i = {z_2}\end{array} \right..\)
Suy ra \(P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = {\left( {\sqrt {{{\left( { - 1} \right)}^2} + {3^2}} } \right)^2} + {\left( {\sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2}} } \right)^2} = 10 + 10 = 20\).
Hướng dẫn giải:
- Giải phương trình tìm nghiệm.
- Tính mô đun và thay và biểu thức \(P\).
Gọi \(S\) là tổng phần thực và phần ảo của số phức $w = {z^3} - i$, biết $z$ thỏa mãn $z + 2 - 4i = \left( {2 - i} \right)\overline {iz} $. Mệnh đề nào sau đây đúng?
Đặt $z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)$, suy ra $iz = i\left( {x + yi} \right) = - y + xi$ $ \Rightarrow \overline {iz} = - y - xi$
Theo giả thiết, ta có $x + yi + 2 - 4i = \left( {2 - i} \right)\left( { - y - xi} \right)$
$ \Leftrightarrow x + 2 + \left( {y - 4} \right)i = \left( { - 2y - x} \right) + \left( {y - 2x} \right)i$ $ \Leftrightarrow \left\{ \begin{array}{l}x + 2 = - 2y - x\\y - 4 = y - 2x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 3\end{array} \right. \Rightarrow z = 2 - 3i$
Khi đó $w = {z^3} - i = {\left( {2 - 3i} \right)^3} - i = - 46 - 10i$.
Hướng dẫn giải:
- Đặt \(z = a + bi\), thay vào đẳng thức bài cho tìm \(z\).
- Từ đó tính \(w\).
Tìm phần ảo \(b\) của số phức $w = 1 + \left( {1 + i} \right) + {\left( {1 + i} \right)^2} + {\left( {1 + i} \right)^3} + ... + {\left( {1 + i} \right)^{2018}}$.
Dễ thấy tổng trên là tổng của cấp số nhân có $2019$ số hạng, trong đó số hạng đầu tiên ${u_1} = 1$, công bội $q = 1 + i$.
Do đó $w = {u_1}.\dfrac{{1 - {q^{2019}}}}{{1 - q}} = 1.\dfrac{{1 - {{\left( {1 + i} \right)}^{2019}}}}{{1 - \left( {1 + i} \right)}} $ $= \dfrac{{1 - {{\left( {1 + i} \right)}^{2019}}}}{{ - i}}$
Ta có ${\left( {1 + i} \right)^2} = 1 + 2i + {i^2} = 2i$.
Suy ra \({\left( {1 + i} \right)^{2019}} = {\left[ {{{\left( {1 + i} \right)}^2}} \right]^{1009}}.\left( {1 + i} \right) = {\left( {2i} \right)^{1009}}\left( {1 + i} \right)\) \( = {2^{1009}}.{i^{1009}}.\left( {1 + i} \right)\) \(= {2^{1009}}.i.\left( {1 + i} \right) = {2^{1009}}.\left( { - 1 + i} \right)\)
Vậy $w = \dfrac{{1 - {{\left( {1 + i} \right)}^{2019}}}}{{ - i}} = \dfrac{{1 - {2^{1009}}.\left( { - 1 + i} \right)}}{{ - i}} = \dfrac{{i.\left[ {1 - {2^{1009}}.\left( { - 1 + i} \right)} \right]}}{1} = {2^{1009}} + \left( {{2^{1009}} + 1} \right)i$
Hướng dẫn giải:
Tổng cần tính là tổng của cấp số nhân có $2019$ số hạng, trong đó số hạng đầu tiên ${u_1} = 1$, công bội $q = 1 + i$.
Sử dụng công thức tính tổng \({S_n} = u_1.\dfrac{{1 - {q^n}}}{{1 - q}}\).
Gọi ${z_1},{z_2}$ là các nghiệm của phương trình: $z + \dfrac{1}{z} = - 1$. Giá trị của $P = {z_1}^3 + {z_2}^3$ là:
Phương trình: $z + \dfrac{1}{z} = - 1 \Leftrightarrow {z^2} + z + 1 = 0$
Ta có: ${z_1} + {z_2} = - 1;{z_1}.{z_2} = 1$
Khi đó $P = {z_1}^3 + {z_2}^3 = \left( {{z_1} + {z_2}} \right)\left( {{z_1}^2 - {z_1}{z_2} + {z_2}^2} \right) = \left( {{z_1} + {z_2}} \right)\left[ {{{\left( {{z_1} + {z_2}} \right)}^2} - 3{z_1}{z_2}} \right] = - 1.(1 - 3) = 2$
Hướng dẫn giải:
- Biến đổi phương trình đưa về phương trình bậc hai.
- Áp dụng định lý Vi-et cho phương trình bậc hai: \(\left\{ \begin{array}{l}{z_1} + {z_2} = - \dfrac{b}{a}\\{z_1}.{z_2} = \dfrac{c}{a}\end{array} \right.\)
- Thay vào biểu thức cần tính giá trị.
Kí hiệu \({z_1},{\rm{ }}{z_2},\,{\rm{ }}{z_3}\) và \({z_4}\) là bốn nghiệm phức của phương trình $6{z^4} + 19{z^2} + 15 = 0.$ Tính tổng \(T = \dfrac{1}{{{z_1}}} + \dfrac{1}{{{z_2}}} + \dfrac{1}{{{z_3}}} + \dfrac{1}{{{z_4}}}.\)
Phương trình $6{z^4} + 19{z^2} + 15 = 0$ $ \Leftrightarrow \left( {2{z^2} + 3} \right)\left( {3{z^2} + 5} \right) = 0$ $ \Leftrightarrow \left[ \begin{array}{l}2{z^2} = - \,3\\3{z^2} = - \,5\end{array} \right.$
$ \Leftrightarrow \left[ \begin{array}{l}{z^2} = - \dfrac{3}{2}\\{z^2} = - \dfrac{5}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{z^2} = \dfrac{{3{i^2}}}{2}\\{z^2} = \dfrac{{5{i^2}}}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = \pm \,\dfrac{{i\sqrt 6 }}{2}\\z = \pm \,\dfrac{{i\sqrt {15} }}{3}\end{array} \right.$ $ \Rightarrow T = \dfrac{2}{{i\sqrt 6 }} - \dfrac{2}{{i\sqrt 6 }} + \dfrac{3}{{i\sqrt {15} }} - \dfrac{3}{{i\sqrt {15} }} = 0$
Hướng dẫn giải:
- Giải phương trình tìm các nghiệm \({z_1},{z_2},{z_3},{z_4}\).
- Thay vào tính giá trị biểu thức và kết luận.
Cho số phức $z = z_1^2 + {\left| {{z_1}} \right|^2}$ với ${z_1}$ là số thuần ảo. Mệnh đề nào sau đây đúng?
Gọi ${z_1} = m.i{\rm{ }}\left( {m \in \mathbb{R}} \right) \Rightarrow \left\{ \begin{array}{l}z_1^2 = {\left( {m.i} \right)^2} = {m^2}.{i^2} = - {m^2}\\\left| {{z_1}} \right| = \sqrt {{0^2} + {m^2}} = \left| m \right| \Rightarrow {\left| {{z_1}} \right|^2} = {m^2}\end{array} \right..$
Khi đó $z = z_1^2 + {\left| {{z_1}} \right|^2} = - {m^2} + {m^2} = 0$.
Hướng dẫn giải:
Đặt ${z_1} = m.i$ thay vào tìm dạng của \(z\) và kết luận.
Cho các số phức \({z_1},{\rm{ }}{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 3,{\rm{ }}\left| {{z_2}} \right| = 4\) và \(\left| {{z_1} - {z_2}} \right| = 5.\) Gọi \(A,{\rm{ }}B\) lần lượt là điểm biểu diển các số phức \({z_1},{\rm{ }}{z_2}\) Tính diện tích \(S\) của tam giác \(OAB\) với \(O\) là gốc tọa độ.
Từ giả thiết, ta có \(OA = 3,{\rm{ }}OB = 4\) và \(AB = 5\).
Ta có \(O{A^2} + O{B^2} = A{B^2}\) \( \Rightarrow \Delta OAB\) vuông tại \(O.\)
Vậy \(S = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.3.4 = 6\).
Hướng dẫn giải:
Chuyển về bài toán hình học và tính toán.
Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức $z$ thỏa mãn điều kiện \(2|z - 1 - 2i| = |3i + 1 - 2\bar z|\).
Giả sử ta có số phức $z = x + yi$. Thay vào điều kiện \(2|z - 1 - 2i| = |3i + 1 - 2\bar z|\) có
\(2|(x + yi) - 1 - 2i| = |3i + 1 - 2(x - yi)| \Leftrightarrow 2|(x - 1) + (y - 2)i| = |(1 - 2x) + (3 + 2y)i|\) \( \Leftrightarrow 2\sqrt {{{(x - 1)}^2} + {{(y - 2)}^2}} = \sqrt {{{(1 - 2x)}^2} + {{(3 + 2y)}^2}} \)
\( \Leftrightarrow 4{(x - 1)^2} + 4{(y - 2)^2} = {(1 - 2x)^2} + {(3 + 2y)^2}\)
\( \Leftrightarrow 4{x^2} - 8x + 4 + 4{y^2} - 16y + 16 = 4{x^2} - 4x + 1 + 4{y^2} + 12y + 9\)
\( \Leftrightarrow 4x + 28y - 10 = 0\)
\( \Leftrightarrow 2x + 14y - 5 = 0\)
Hướng dẫn giải:
Phương pháp tìm tập hợp điểm biểu diễn số phức
Bước 1: Gọi số phức \(z = x + yi\) có điểm biểu diễn là \(M(x;y)\)
Bước 2: Thay \(z\) vào đề bài \( \Rightarrow \) Sinh ra một phương trình:
+) Đường thẳng: \(Ax + By + C = 0.\)
+) Đường tròn: \({x^2} + {y^2} - 2ax - 2by + c = 0.\)
+) Parabol: \(y = a.{x^2} + bx + c\)
+) Elip: \(\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} = 1\)
Cho số phức \({z_1}\) thỏa mãn \({\left| {{z_1} - 2} \right|^2} - {\left| {{z_1} + i} \right|^2} = 1\) và số phức \({z_2}\) thỏa mãn \(\left| {{z_2} - 4 - i} \right| = \sqrt 5 \). Tìm giá trị nhỏ nhất của \(P = \left| {{z_1} - {z_2}} \right|\).
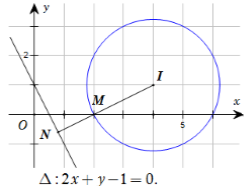
Gọi \(z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)\). Ta có
${{\left| z-2 \right|}^{2}}-{{\left| z+i \right|}^{2}}=1$ $\to {{\left( x-2 \right)}^{2}}+{{y}^{2}}-{{x}^{2}}-{{\left( y+1 \right)}^{2}}=1$ $\xrightarrow{{}}2x+y-1=0$.
Suy ra tập hợp các số phức \({z_1}\) là đường thẳng $\Delta :2x + y - 1 = 0.$
$\left| z-4-i \right|=\sqrt{5}\xrightarrow{{}}\left| \left( x-4 \right)+\left( y-1 \right)i \right|=\sqrt{5}$
$\Leftrightarrow {{\left( x-4 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=5$
Suy ra tập hợp các số phức \({z_2}\) là đường tròn $\left( C \right):{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 5$ có tâm \(I\left( {4;1} \right)\) và bán kính \(R = \sqrt 5 .\)
Khi đó biểu thức \(P = \left| {{z_1} - {z_2}} \right|\) là khoảng cách từ một điểm thuộc \(\Delta \) đến một điểm thuộc \(\left( C \right)\).
Từ đó suy ra \({P_{\min }} = MN = \left| {d\left[ {I,\Delta } \right] - R} \right| \) \(= \left| {\dfrac{8}{{\sqrt 5 }} - \sqrt 5 } \right| = \dfrac{{3\sqrt 5 }}{5}.\)
Hướng dẫn giải:
- Gọi \(z = x + yi\) thay vào điều kiện bài cho.
- Sử dụng phương pháp hình học tìm giá trị nhỏ nhất của \(P\).
Cho số phức \(z\) thỏa mãn \(\left| {{z^2} - 2z + 5} \right| = \left| {\left( {z - 1 + 2i} \right)\left( {z + 3i - 1} \right)} \right|\). Tìm giá trị nhỏ nhất của \(P = \left| w \right|\), với \(w = z - 2 + 2i\).
Ta có $\left| {{z^2} - 2z + 5} \right| = \left| {\left( {z - 1 + 2i} \right)\left( {z + 3i - 1} \right)} \right|$
$ \Leftrightarrow \left| {{{\left( {z - 1} \right)}^2} + 4} \right| = \left| {\left( {z - 1 + 2i} \right)} \right|\left| {\left( {z + 3i - 1} \right)} \right| \Leftrightarrow \left| {{{\left( {z - 1} \right)}^2} - {{\left( {2i} \right)}^2}} \right| = \left| {\left( {z - 1 + 2i} \right)} \right|\left| {\left( {z + 3i - 1} \right)} \right|$
\( \Leftrightarrow \left| {\left( {z - 1 + 2i} \right)\left( {z - 1 - 2i} \right)} \right| = \left| {\left( {z - 1 + 2i} \right)} \right|\left| {\left( {z + 3i - 1} \right)} \right| \Leftrightarrow \left[ \begin{array}{l}z - 1 + 2i = 0{\rm{ }}(1)\\\left| {\left( {z - 1 - 2i} \right)} \right| = \left| {\left( {z + 3i - 1} \right)} \right|{\rm{ }}(2)\end{array} \right..\)
Từ $\left( 1 \right) \Rightarrow z = 1 - 2i \Rightarrow w = - 1 \Rightarrow P = \left| w \right| = 1.$
Xét $\left( 2 \right)$. Gọi \(z = x + yi{\rm{ }}\left( {x;y \in \mathbb{R}} \right)\).
Ta có $\left| {\left( {z - 1 - 2i} \right)} \right| = \left| {\left( {z + 3i - 1} \right)} \right| $ $ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} $ $\Leftrightarrow y = - \dfrac{1}{2}.$
Khi đó $w = x - \dfrac{1}{2}i - 2 + 2i = \left( {x - 2} \right) + \dfrac{3}{2}i$ $ \Rightarrow P = \left| w \right| = \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {\dfrac{3}{2}} \right)}^2}} \ge \dfrac{3}{2}$
Vậy \({P_{\min }} =1.\)
Hướng dẫn giải:
- Biến đổi thu gọn biểu thức bài cho về đơn giản hơn.
- Đánh giá giá trị nhỏ nhất của \(\left| w \right|\) và kết luận.
Giải thích thêm:
Bài này ta có thể giải theo cách hình học từ bước xét phương trình (2):
Điểm M(x;y) biểu diễn số phức z=x+yi thỏa mãn $|z-1-2i|=|z+3i-1|$
Tương đương với $|z-(1+2i)|=|z-(1-3i)|$ (*)
Gọi A(1;2) biểu diễn số phức z=1+2i; B(1;-3)
Khi đó $|z-(1+2i)|=MA$;$|z-(1-3i)|=MB$
(*)<=>$MA=MB$.
Khi đó tập hợp điểm M thỏa mãn $MA=MB$ là đường trung trực của AB. Ta tìm đường trung trực của AB thì sẽ được tập hợp điểm M là đường thẳng $y=-\dfrac{1}{2}$
Gọi N(2;-2) biểu diễn số phức z=2-2i.
Khi đó $P=|w|=|z-2+2i|=MN$
GTNN của P là khoảng cách từ N đến đường thẳng $y=-\dfrac{1}{2}$ và bằng $\dfrac{3}{2}$
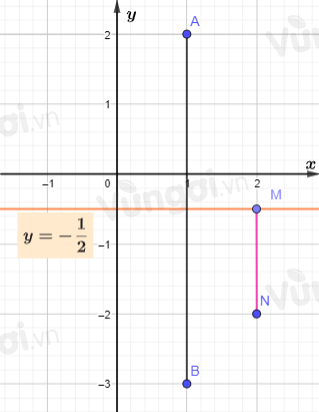
Tuy nhiên khi kết hợp với trường hợp 1 thì đán án vẫn là $P_{min}=1$
Trong các số phức z thỏa mãn \(\left| {z + 3 + 4i} \right| = 2\) , gọi \({z_0}\) là số phức có mô đun nhỏ nhất. Khi đó:
Giả sử $z = a + bi\left( {a,b \in R} \right)$ ta có:
$\left| {z + 3 + 4i} \right| = 2 \Leftrightarrow \left| {(a + 3) + (b + 4)i} \right| = 2 \Leftrightarrow {(a + 3)^2} + {(b + 4)^2} = 4$
Do đó tập hợp điểm biểu diễn số phức $z$ thuộc đường tròn tâm $I\left( { - 3; - 4} \right)$ và bán kính $r = 2$
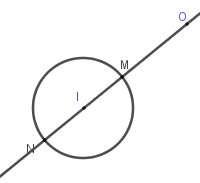
Từ hình vẽ ta thấy số phức \({z_0}\) có mô đun nhỏ nhất nếu \({z_0}\) có điểm biểu diễn là \(M\).
Ta có: $\overrightarrow {OI} = ( - 3; - 4)$ nên đường thẳng đi qua \(O\) và \(I\) là $OI:\left\{ \begin{array}{l}x = 3t\\y = 4t\end{array} \right. \Rightarrow M\left( {3t;4t} \right)$
Mặt khác $M \in \left( C \right)$ nên: ${\left( {3t + 3} \right)^2} + {\left( {4t + 4} \right)^2} = 4 \Leftrightarrow 25{t^2} + 50t + 21 = 0 \Leftrightarrow \left\{ \begin{array}{l}t = \dfrac{{ - 3}}{5}\\t = \dfrac{{ - 7}}{5}\end{array} \right.$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ hoặc $M\left( {\dfrac{{ - 21}}{5};\dfrac{{ - 28}}{5}} \right)$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ thuộc $\left( C \right)$ và gần $O$ nhất.
$ \Rightarrow z = \dfrac{{ - 9}}{5} - \dfrac{{12}}{5}i \Rightarrow \left| z \right| = 3$
Hướng dẫn giải:
- Bước 1: Gọi số phức \(z = x + yi\left( {x,y \in R} \right)\)
- Bước 2: Thay \(z\) và biểu thức đã cho tìm mối quan hệ của \(x,y\) suy ra tập hợp biểu diễn của số phức \(z\).
- Bước 3: Sử dụng mối quan hệ hình học để tìm mô đun số phức cần tìm.
Đề thi liên quan
-
Đề kiểm tra 15 phút chương 4: Số phức - Đề số 1
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 4: Số phức - Đề số 2
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 4: Số phức - Đề số 3
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 4: Số phức - Đề số 1
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 4: Số phức - Đề số 2
-
25 câu hỏi
-
45 phút
-

