Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
Giả sử $z = a + bi\left( {a,b \in R} \right)$ ta có:
$\left| {z + 3 + 4i} \right| = 2 \Leftrightarrow \left| {(a + 3) + (b + 4)i} \right| = 2 \Leftrightarrow {(a + 3)^2} + {(b + 4)^2} = 4$
Do đó tập hợp điểm biểu diễn số phức $z$ thuộc đường tròn tâm $I\left( { - 3; - 4} \right)$ và bán kính $r = 2$
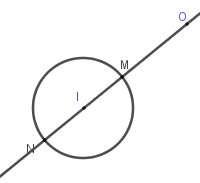
Từ hình vẽ ta thấy số phức \({z_0}\) có mô đun nhỏ nhất nếu \({z_0}\) có điểm biểu diễn là \(M\).
Ta có: $\overrightarrow {OI} = ( - 3; - 4)$ nên đường thẳng đi qua \(O\) và \(I\) là $OI:\left\{ \begin{array}{l}x = 3t\\y = 4t\end{array} \right. \Rightarrow M\left( {3t;4t} \right)$
Mặt khác $M \in \left( C \right)$ nên: ${\left( {3t + 3} \right)^2} + {\left( {4t + 4} \right)^2} = 4 \Leftrightarrow 25{t^2} + 50t + 21 = 0 \Leftrightarrow \left\{ \begin{array}{l}t = \dfrac{{ - 3}}{5}\\t = \dfrac{{ - 7}}{5}\end{array} \right.$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ hoặc $M\left( {\dfrac{{ - 21}}{5};\dfrac{{ - 28}}{5}} \right)$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ thuộc $\left( C \right)$ và gần $O$ nhất.
$ \Rightarrow z = \dfrac{{ - 9}}{5} - \dfrac{{12}}{5}i \Rightarrow \left| z \right| = 3$
Hướng dẫn giải:
- Bước 1: Gọi số phức \(z = x + yi\left( {x,y \in R} \right)\)
- Bước 2: Thay \(z\) và biểu thức đã cho tìm mối quan hệ của \(x,y\) suy ra tập hợp biểu diễn của số phức \(z\).
- Bước 3: Sử dụng mối quan hệ hình học để tìm mô đun số phức cần tìm.
Giả sử $z = a + bi\left( {a,b \in R} \right)$ ta có:
$\left| {z + 3 + 4i} \right| = 2 \Leftrightarrow \left| {(a + 3) + (b + 4)i} \right| = 2 \Leftrightarrow {(a + 3)^2} + {(b + 4)^2} = 4$
Do đó tập hợp điểm biểu diễn số phức $z$ thuộc đường tròn tâm $I\left( { - 3; - 4} \right)$ và bán kính $r = 2$

Từ hình vẽ ta thấy số phức \({z_0}\) có mô đun nhỏ nhất nếu \({z_0}\) có điểm biểu diễn là \(M\).
Ta có: $\overrightarrow {OI} = ( - 3; - 4)$ nên đường thẳng đi qua \(O\) và \(I\) là $OI:\left\{ \begin{array}{l}x = 3t\\y = 4t\end{array} \right. \Rightarrow M\left( {3t;4t} \right)$
Mặt khác $M \in \left( C \right)$ nên: ${\left( {3t + 3} \right)^2} + {\left( {4t + 4} \right)^2} = 4 \Leftrightarrow 25{t^2} + 50t + 21 = 0 \Leftrightarrow \left\{ \begin{array}{l}t = \dfrac{{ - 3}}{5}\\t = \dfrac{{ - 7}}{5}\end{array} \right.$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ hoặc $M\left( {\dfrac{{ - 21}}{5};\dfrac{{ - 28}}{5}} \right)$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ thuộc $\left( C \right)$ và gần $O$ nhất.
$ \Rightarrow z = \dfrac{{ - 9}}{5} - \dfrac{{12}}{5}i \Rightarrow \left| z \right| = 3$
Hướng dẫn giải:
- Bước 1: Gọi số phức \(z = x + yi\left( {x,y \in R} \right)\)
- Bước 2: Thay \(z\) và biểu thức đã cho tìm mối quan hệ của \(x,y\) suy ra tập hợp biểu diễn của số phức \(z\).
- Bước 3: Sử dụng mối quan hệ hình học để tìm mô đun số phức cần tìm.
CÂU HỎI CÙNG CHỦ ĐỀ
Gọi ${z_1},{z_2}$ là các nghiệm của phương trình: $z + \dfrac{1}{z} = - 1$. Giá trị của $P = {z_1}^3 + {z_2}^3$ là:
Với hai số phức bất kì ${z_1},{z_2}$ , khẳng định nào sau đây đúng:
Nghiệm của phương trình: ${z^2} + (1 - i)z - 18 + 13i = 0$ là:
Gọi \(A\) là điểm biểu diễn của số phức \(z = 3 + 2i\) và \(B\) là điểm biểu diễn của số phức \(z' = 2 + 3i\). Mệnh đề nào sau đây là đúng?
Gọi \({z_1}\) và \({z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 10 = 0\). Tính giá trị biểu thức \(P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}.\)
Gọi \(S\) là tổng phần thực và phần ảo của số phức $w = {z^3} - i$, biết $z$ thỏa mãn $z + 2 - 4i = \left( {2 - i} \right)\overline {iz} $. Mệnh đề nào sau đây đúng?
Cho hai số phức ${z_1} = 1 + i$ và ${z_2} = 2 - 3i$. Tính môđun của số phức ${z_1} - {z_2}.$
Tìm phần ảo \(b\) của số phức $w = 1 + \left( {1 + i} \right) + {\left( {1 + i} \right)^2} + {\left( {1 + i} \right)^3} + ... + {\left( {1 + i} \right)^{2018}}$.
Biết rằng có duy nhất một cặp số thực $\left( {x;y} \right)$ thỏa mãn $\left( {x + y} \right) + \left( {x - y} \right)i = 5 + 3i$. Tính \(S = x + y.\)
Cho số phức $z = z_1^2 + {\left| {{z_1}} \right|^2}$ với ${z_1}$ là số thuần ảo. Mệnh đề nào sau đây đúng?
Cho các số phức \({z_1},{\rm{ }}{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 3,{\rm{ }}\left| {{z_2}} \right| = 4\) và \(\left| {{z_1} - {z_2}} \right| = 5.\) Gọi \(A,{\rm{ }}B\) lần lượt là điểm biểu diển các số phức \({z_1},{\rm{ }}{z_2}\) Tính diện tích \(S\) của tam giác \(OAB\) với \(O\) là gốc tọa độ.
Kí hiệu \({z_1},{\rm{ }}{z_2},\,{\rm{ }}{z_3}\) và \({z_4}\) là bốn nghiệm phức của phương trình $6{z^4} + 19{z^2} + 15 = 0.$ Tính tổng \(T = \dfrac{1}{{{z_1}}} + \dfrac{1}{{{z_2}}} + \dfrac{1}{{{z_3}}} + \dfrac{1}{{{z_4}}}.\)

