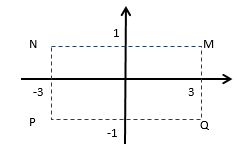
\(\left( {2 - i} \right)z = 7 - i \Rightarrow z = \dfrac{{7 - i}}{{2 - i}} = \dfrac{{(7 - i)(2 + i)}}{5} = \dfrac{{15 + 5i}}{5} = 3 + i\)

Suy ra điểm có tọa độ $\left( {3;1} \right)$ sẽ biểu diễn số phức $z$, suy ra $M$ thỏa mãn.

Ta có: \(\left\{ \begin{array}{l}{z_1} + {z_2} =  - \dfrac{B}{A} = \dfrac{{ - 2i}}{1} =  - 2i\\{z_1}{z_2} = \dfrac{C}{A} = \dfrac{i}{1} = i\end{array} \right.\)

Vậy \({z_1} + {z_2} =  - 2i\).

$\overline z = 2 - 5i \Rightarrow w = i\left( {2 + 5i} \right) + 2 - 5i =  - 3 - 3i$.

Căn bậc hai của số \(a =  - 3\) là \(i\sqrt 3 \) và \( - i\sqrt 3 \).

\(\Delta ' = 1 - 2 =  - 1 < 0 \Rightarrow \) phương trình có hai nghiệm là \(z = 1 + i\) và \(z = 1 - i\).

Vậy phương trình có hai nghiệm phức.

Do đó các đáp án A, B, D đều đúng

Ta có: $z = 1 + \sqrt 3 i \Rightarrow \dfrac{1}{z} = \dfrac{1}{{1 + \sqrt 3 i}} = \dfrac{{1 - \sqrt 3 i}}{{(1 - \sqrt 3 i)(1 + \sqrt 3 i)}} $

$= \dfrac{{1 - \sqrt 3 i}}{{{1^2} - {{(\sqrt 3 i)}^2}}} = \dfrac{{1 - \sqrt 3 i}}{4} = \dfrac{1}{4} - \dfrac{{\sqrt 3 }}{4}i$

Số phức liên hợp của $z$ là $3 + 2i$, phần thực $3$, phần ảo $2$. 

Đáp án A: 

\(\begin{array}{l}{z^2} = {a^2} + 2abi - {b^2}\\ \Leftrightarrow {z^2} = {a^2} + 2.a.bi + {b^2}.{i^2} = {\left( {a + bi} \right)^2}\\ \Leftrightarrow z =  \pm \left( {a + bi} \right)\end{array}\)

Vậy có 2 nghiệm $z = a + bi$ hoặc $z =  - a - bi$ (Loại).

Đáp án B: $z =  \pm \sqrt {{a^2} + {b^2}} $ (loại)

Đáp án C: 

\(\begin{array}{l}{z^2} - 2az + {a^2} + {b^2} = 0\\ \Leftrightarrow {\left( {z - a} \right)^2} =  - {b^2}\\ \Leftrightarrow {\left( {z - a} \right)^2} = {b^2}{i^2}\\ \Leftrightarrow \left[ \begin{array}{l}z - a = bi\\z - a =  - bi\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = a + bi\\z = a - bi\end{array} \right.\end{array}\)

Vậy phương trình bậc hai trên có nghiệm $z = a + bi;z = a - bi$ (thỏa mãn)

Đáp án D: Giải phương trình ta được hai nghiệm $a \pm b$ nên loại.

Hai số phức \(z = a + bi,z' = a + b'i\) bằng nhau nếu \(b = b'\)

${\rm{w}} = (3 + 2i)z + 2\overline z  = (3 + 2i)(2 + 3i) + 2.(2 - 3i) $

$= 6 - 6 + 4i + 9i + 4 - 6i = 4 + 7i$

Ta có $z = 1 + 2i$ là nghiệm của phương trình nên ta có:

$\begin{array}{l}{(1 + 2i)^2} + b(1 + 2i) + c = 0 \Leftrightarrow  - 3 + 4i + b + 2bi + c = 0\\ \Leftrightarrow ( - 3 + b + c) + (4 + 2b)i = 0\\ \Leftrightarrow \left\{ \begin{array}{l} - 3 + b + c = 0\\4 + 2b = 0\end{array} \right. \Leftrightarrow b + c = 3\end{array}$

Số phức \(w = x + yi\left( {x,y \in R} \right)\) là căn bậc hai của số phức \(z = a + bi\) nếu \({w^2} = z\).

Số phức $3 - 2\sqrt 2 i$ có phần thực bằng $3$ phần ảo bằng $ - 2\sqrt 2 $ hay $\left\{ \begin{array}{l}a = 3\\b =  - 2\sqrt 2 \end{array} \right.$

Phương trình bậc hai có thể có \(1\) nghiệm nếu \(\Delta  = 0\)  hoặc \(2\) nghiệm nếu \(\Delta  \ne 0\).

$z = 1 + i + {i^2} + {i^3} + ... + {i^9} = 1 + i - 1 - i + 1 + i - 1 - i + 1 + i = 1 + i$

Ta có: $\overline z  = \left( {4 - 3i} \right)\left( {1 + i} \right) = 7 + i \Rightarrow z = 7 - i \Rightarrow \left| z \right| = \sqrt {50}  = 5\sqrt 2 $

\(z = a + bi \) \(\Rightarrow {z^2} = {\left( {a + bi} \right)^2} \) \(= {a^2} + 2abi + {b^2}{i^2} \) \(= {a^2} - {b^2} + 2abi\)

\(w = \dfrac{1}{{{{\left( {a + bi} \right)}^2}}} \) \(= \dfrac{1}{{{a^2} - {b^2} + 2abi}} \) $ = \dfrac{{{a^2} - {b^2} - 2abi}}{{\left( {{a^2} - {b^2} + 2abi} \right)\left( {{a^2} - {b^2} - 2abi} \right)}}$ \(= \dfrac{{{a^2} - {b^2} - 2abi}}{{{{\left( {{a^2} - {b^2}} \right)}^2} - {{\left( {2abi} \right)}^2}}} \)

\( = \dfrac{{{a^2} - {b^2} - 2abi}}{{{a^4} + {b^4} - 2{a^2}{b^2} - 4{a^2}{b^2}{i^2}}} \) \(= \dfrac{{{a^2} - {b^2} - 2abi}}{{{a^4} + {b^4} - 2{a^2}{b^2} + 4{a^2}{b^2}}} \) \(= \dfrac{{{a^2} - {b^2} - 2abi}}{{{a^4} + {b^4} + 2{a^2}{b^2}}} \) \(= \dfrac{{{a^2} - {b^2} - 2abi}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}}\)

\(= \dfrac{{{a^2} - {b^2}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}} - \dfrac{{2ab}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}}i\)

Nên phần thực của số phức $w$ là : \(\dfrac{{{a^2} - {b^2}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}}\).

$\begin{array}{l}{z^4} - {z^2} - 12 = 0 \Leftrightarrow \left( {{z^2} - 4} \right)\left( {{z^2} + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}z =  \pm 2\\z =  \pm i\sqrt 3 \end{array} \right.\\ \Rightarrow T = 2 + 2 + \sqrt 3  + \sqrt 3  = 4 + 2\sqrt 3 \end{array}$

$\begin{array}{l}{z^2} + z + 1 = 0\\\Delta  = 1 - 4 =  - 3 = 3{i^2}\\z = \dfrac{{ - 1 \pm i\sqrt 3 }}{2}\end{array}$

$z =  - \dfrac{1}{2} \pm \dfrac{{\sqrt 3 }}{2}i $

$\Rightarrow P = {( - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i)^2} + {( - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i)^2} + ( - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i)\left( { - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i} \right)$

$= - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i + \dfrac{1}{4} + \dfrac{3}{4} = 0$

\(2{z^4} - 3{z^2} - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}{z^2} = 2\\{z^2} =  - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z =  \pm \sqrt 2 \\z =  \pm i\dfrac{{\sqrt 2 }}{2}\end{array} \right.\)\(T = |{z_1}{|^2} + |{z_2}{|^2} + |{z_3}{|^2} + |{z_4}{|^2} = 2 + 2 + \dfrac{1}{2} + \dfrac{1}{2} = 5\)

Ta có: ${z_2} = 2i$

Có $A\left( {1;1} \right);B\left( {0;2} \right)$ và $C\left( {m; - 1} \right)$

\(\overrightarrow {AB}  = ( - 1;1);\overrightarrow {BC}  = (m; - 3) \Rightarrow \overrightarrow {AB} .\overrightarrow {BC}  =  - 1.m - 3 = 0 \Leftrightarrow m =  - 3\)

Đặt \(z = a + bi\)

Ta có: $\left| {z - i} \right| = 5 \Leftrightarrow \left| {a + bi - i} \right| = 5 $ $\Leftrightarrow \left| {a + \left( {b - 1} \right)i} \right| = 5 \Leftrightarrow \sqrt {{a^2} + {{\left( {b - 1} \right)}^2}} = 5 $ $\Leftrightarrow {a^2} + {\left( {b - 1} \right)^2} = 25$ (1)

${z^2} = (a+bi)^2={a^2} + 2{\rm{a}}bi - {b^2}=a^2-b^2+2abi$

Do \({z^2}\) là số thuần ảo nên:${a^2} - {b^2} = 0 \Leftrightarrow \left( {a - b} \right)\left( {a + b} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
b = a\\
b = - a
\end{array} \right.$

TH1: b=a thay vào (1) ta được:

${a^2} + {\left( {a - 1} \right)^2} = 25 $ $\Leftrightarrow {a^2} + {a^2} - 2a + 1 = 25$ $ \Leftrightarrow 2{a^2} - 2a - 24 = 0 $ $\Leftrightarrow \left[ \begin{array}{l}
a = 4 \Rightarrow b = 4\\
a = - 3 \Rightarrow b = - 3
\end{array} \right.$

TH2: b=-a thay vào (1) ta được:

${a^2} + {\left( { - a - 1} \right)^2} = 25$ $ \Leftrightarrow {a^2} + {a^2} + 2a + 1 = 25 $ $\Leftrightarrow 2{a^2} + 2a - 24 = 0 $ $\Leftrightarrow \left[ \begin{array}{l}
a = 3 \Rightarrow b = - 3\\
a = - 4 \Rightarrow b = 4
\end{array} \right.$

Vậy có $4$ số phức cần tìm là: $4+4i, -3-3i,$ $3-3i, -4+4i$.

Có \(\dfrac{{ - 2 - 3i}}{{3 - 2i}} =  - i\). Đặt \(z = x + yi\) thì

\(\dfrac{{ - 2 - 3i}}{{3 - 2i}}z + 1 =  - i(x + yi) + 1 = (y + 1) - xi\)

Điều kiện đã cho trong bài được viết lại thành \({(y + 1)^2} + {x^2} = 1\)

Điểm biểu diễn \(M(x,y)\) của \(z\) chạy trên đường tròn (*) có tâm $I\left( {0, - 1} \right)$, bán kính bằng $1$.

Cần tìm điểm \(M(x,y)\) thuộc đường tròn này để $OM$ lớn nhất.

Vì \(O\) nằm trên đường tròn nên $OM$ lớn nhất khi $OM$ là đường kính của (*) \( \Leftrightarrow \) $I$ là trung điểm của $OM$ \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2{x_I}}&{}\\{y = 2{y_I}}&{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}&{}\\{y =  - 2}&{}\end{array}} \right. \Leftrightarrow M(0, - 2)\). Suy ra \(z =  - 2i \Leftrightarrow |z| = 2\)

Vậy $\max \left| z \right| = 2$

Gọi $z = x + yi$;

Khi đó $z - 4 + 3i = \left( {x - 4} \right) + \left( {y + 3} \right)i$

$ \Rightarrow \left| {z - 4 + 3i} \right| = \left| {\left( {x - 4} \right) + \left( {y + 3} \right)i} \right| = 3 \Rightarrow {\left( {x - 4} \right)^2} + {\left( {y + 3} \right)^2} = 9$

Vậy quỹ tích các điểm \(M\) biểu diễn số phức \(z\) thuộc đường tròn tâm $I\left( {4; - 3} \right);R = 3$.

Đặt  $\left\{ \begin{array}{l}x = 3\sin t + 4\\y = 3\cos t - 3\end{array} \right.$

$ \Rightarrow {x^2} + {y^2} = {\left( {3\sin t + 4} \right)^2} + {\left( {3\cos t - 3} \right)^2} $

$= 9{\sin ^2}t + 9{\cos ^2}t + 24\sin t - 18\cos t + 25 = 24\sin t - 18\cos t + 34$

Mà $24\sin t - 18\cos t \le \sqrt {\left( {{{24}^2} + {{18}^2}} \right)\left( {{{\sin }^2}t + {{\cos }^2}t} \right)}  = 30$ (theo bunhiacopxki)

$ \Rightarrow {x^2} + {y^2} \le 30 + 34 = 64 \Rightarrow \sqrt {{x^2} + {y^2}}  \le 8 \Rightarrow \left| z \right| \le 8$

Gọi $z=x+yi\left( x,y\in R \right)$

Trên mặt phẳng tọa độ $Oxy$ gọi $P\left( {x;y} \right)$ là điểm biểu diễn của số phức $z$

Gọi $A\left( {-2;1} \right),B\left( {4;7} \right)$ thì

$\begin{array}{l}AB = 6\sqrt 2  = \left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right|\\ = \sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y - 1} \right)}^2}}  + \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 7} \right)}^2}}  = PA + PB\end{array}$

Suy ra tập hợp các điểm $P$ thỏa mãn chính là đoạn thẳng AB

Có $\left| {z - 1 + i} \right| = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}}  = PC$ với $C\left( {1;-1} \right)$

Do đó \(P{C_{\min }}\) khi \(P\) là hình chiếu của \(C\) lên \(AB\) và \(P{C_{\max }}\) khi \(P \equiv B\)

Suy ra $M = CB = \sqrt {73} $.

Ta có: \(AB:\dfrac{{x + 2}}{{4 + 2}} = \dfrac{{y - 1}}{{7 - 1}} \Leftrightarrow x - y + 3 = 0\)\( \Rightarrow m=d\left( {C,AB} \right) = \dfrac{{\left| {1 - \left( { - 1} \right) + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{5}{{\sqrt 2 }}\)

$\Rightarrow M + m = \dfrac{{5\sqrt 2  + 2\sqrt {73} }}{2}$