Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiXét số phức \(z\) thỏa mãn \(\left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right| = 6\sqrt 2 \). Gọi \(m,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \(\left| {z - 1 + i} \right|\). Tính \(P = m + M\).
A.
\(P = \sqrt {13} + \sqrt {73} \)
B.
\(P = \dfrac{{5\sqrt 2 + 2\sqrt {73} }}{2}\)
C.
\(P = 5\sqrt 2 + \sqrt {73} \)
D.
\(P = \dfrac{{5\sqrt 2 + \sqrt {73} }}{2}\)
Lời giải của giáo viên
ToanVN.com
Đáp án đúng: b
Gọi $z=x+yi\left( x,y\in R \right)$
Trên mặt phẳng tọa độ $Oxy$ gọi $P\left( {x;y} \right)$ là điểm biểu diễn của số phức $z$
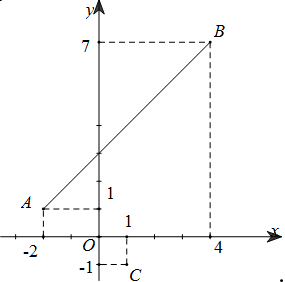
Gọi $A\left( {-2;1} \right),B\left( {4;7} \right)$ thì
$\begin{array}{l}AB = 6\sqrt 2 = \left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right|\\ = \sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y - 1} \right)}^2}} + \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 7} \right)}^2}} = PA + PB\end{array}$
Suy ra tập hợp các điểm $P$ thỏa mãn chính là đoạn thẳng AB
Có $\left| {z - 1 + i} \right| = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} = PC$ với $C\left( {1;-1} \right)$
Do đó \(P{C_{\min }}\) khi \(P\) là hình chiếu của \(C\) lên \(AB\) và \(P{C_{\max }}\) khi \(P \equiv B\)
Suy ra $M = CB = \sqrt {73} $.
Ta có: \(AB:\dfrac{{x + 2}}{{4 + 2}} = \dfrac{{y - 1}}{{7 - 1}} \Leftrightarrow x - y + 3 = 0\)\( \Rightarrow m=d\left( {C,AB} \right) = \dfrac{{\left| {1 - \left( { - 1} \right) + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{5}{{\sqrt 2 }}\)
$\Rightarrow M + m = \dfrac{{5\sqrt 2 + 2\sqrt {73} }}{2}$
Hướng dẫn giải:
- Gọi $z = x + yi$ và tìm tập hợp điểm biểu diễn số phức $z$ thỏa mãn bài toán.
- Biểu diễn tập hợp điểm đó trên hệ trục tọa độ từ đó tìm GTLN, GTNN của biểu thức đã cho.
Gọi $z=x+yi\left( x,y\in R \right)$
Trên mặt phẳng tọa độ $Oxy$ gọi $P\left( {x;y} \right)$ là điểm biểu diễn của số phức $z$
Gọi $A\left( {-2;1} \right),B\left( {4;7} \right)$ thì
$\begin{array}{l}AB = 6\sqrt 2 = \left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right|\\ = \sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y - 1} \right)}^2}} + \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 7} \right)}^2}} = PA + PB\end{array}$
Suy ra tập hợp các điểm $P$ thỏa mãn chính là đoạn thẳng AB
Có $\left| {z - 1 + i} \right| = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} = PC$ với $C\left( {1;-1} \right)$
Do đó \(P{C_{\min }}\) khi \(P\) là hình chiếu của \(C\) lên \(AB\) và \(P{C_{\max }}\) khi \(P \equiv B\)
Suy ra $M = CB = \sqrt {73} $.
Ta có: \(AB:\dfrac{{x + 2}}{{4 + 2}} = \dfrac{{y - 1}}{{7 - 1}} \Leftrightarrow x - y + 3 = 0\)\( \Rightarrow m=d\left( {C,AB} \right) = \dfrac{{\left| {1 - \left( { - 1} \right) + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{5}{{\sqrt 2 }}\)
$\Rightarrow M + m = \dfrac{{5\sqrt 2 + 2\sqrt {73} }}{2}$
Hướng dẫn giải:
- Gọi $z = x + yi$ và tìm tập hợp điểm biểu diễn số phức $z$ thỏa mãn bài toán.
- Biểu diễn tập hợp điểm đó trên hệ trục tọa độ từ đó tìm GTLN, GTNN của biểu thức đã cho.
CÂU HỎI CÙNG CHỦ ĐỀ
Tính môđun của số phức $z$ biết $\overline z = \left( {4 - 3i} \right)\left( {1 + i} \right)$.
Phương trình bậc hai trên tập số phức có thể có mấy nghiệm?
Biết rằng phương trình ${z^2} + bz + c = 0\left( {b;c \in R} \right)$ có một nghiệm phức là ${z_1} = 1 + 2i$ . Khi đó:
Số phức \(w\) là căn bậc hai của số phức \(z\) nếu:
Gọi \({z_1};{z_2};{z_3};{z_4}\) là bốn nghiệm phức của phương trình \(2{z^4} - 3{z^2} - 2 = 0\). Tổng \(T = |{z_1}{|^2} + |{z_2}{|^2} + |{z_3}{|^2} + |{z_4}{|^2}\) bằng:
Hai số phức \(z = a + bi,z' = a + b'i\) bằng nhau nếu:
Cho số phức $z = 1 + i + {i^2} + {i^3} + ... + {i^9}$. Khi đó:
Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện $\left| {z - i} \right| = 5$ và \({z^2}\) là số thuần ảo?
Cho số phức \(z = a + bi(ab \ne 0)\). Tìm phần thực của số phức \({\rm{w}} = \dfrac{1}{{{z^2}}}\).
Tìm giá trị lớn nhất của \(|z|\), biết rằng \(z\) thỏa mãn điều kiện \(|\dfrac{{ - 2 - 3i}}{{3 - 2i}}z + 1| = 1\).
Cho số phức $z = 3-2i$. Tìm phần thực và phần ảo của số phức \(\overline z \)
Kí hiệu \(a,b\) lần lượt là phần thực và phần ảo của số phức \(3 - 2\sqrt 2 i\). Tìm \(a,b.\)
Cho số phức $z$ thỏa mãn $\left( {2-i} \right)z = 7-i$ . Hỏi điểm biểu diễn của $z$ là điểm nào trong các điểm $M,N,P,Q$ ở hình dưới.
