Ôn tập chương 5

Lý thuyết về ôn tập chương 5 Hệ thức lượng trong tam giác vuông; hệ thức về cạnh và đường cao, các tỉ số lượng giác, công thức lượng giác, hệ thức về cạnh và góc trong tam giác vuông môn toán lớp 9 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(381) 1269 24/09/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Sơ đồ tư duy Ôn tập chương 5

    II. Ôn tập chương 5: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG

    1. Hệ thức về cạnh và đường cao trong tam giác vuông

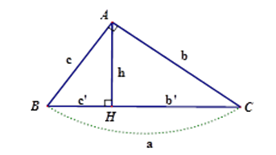
    Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Khi đó ta có các hệ thức sau:

    +) $A{B^2} = BH.BC$ hay ${c^2} = a.c'$

    +) $A{C^2} = CH.BC$ hay ${b^2} = ab'$

    +) $AB.AC = BC.AH$ hay $cb = ah$

    +) $H{A^2} = HB.HC$ hay ${h^2} = c'b'$

    +) $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$ hay $\dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{b^2}}}$.

    +) $B{C^2} = A{B^2} + A{C^2}$ (Định lí Pitago).

    2. Tỉ số lượng giác của góc nhọn

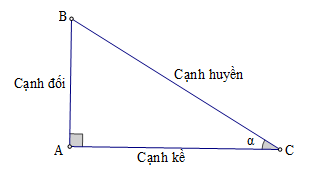
    Các tỉ số lượng giác của góc nhọn \(\alpha \) (hình) được định nghĩa như sau:

    \(\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}};\tan \alpha  = \dfrac{{AB}}{{AC}};\cot \alpha  = \dfrac{{AC}}{{AB}}\)

    + Nếu \(\alpha \) là một góc nhọn bất kỳ  thì

    \(0 < \sin \alpha  < 1;0 < \cos \alpha  < 1\), \(\tan \alpha  > 0;\cot \alpha  > 0\) ,  \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1;\tan \alpha .\cot \alpha  = 1\)

    $\tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }};$$\cot \alpha  = \dfrac{{\cos \alpha }}{{\sin \alpha }};$

    $1 + {\tan ^2}\alpha  = \dfrac{1}{{{{\cos }^2}\alpha }};$$1 + {\cot ^2}\alpha  = \dfrac{1}{{{{\sin }^2}\alpha }}$

    Chú ý: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

    Với hai góc \(\alpha ,\beta \) mà \(\alpha  + \beta  = {90^0}\),

    Ta có: \(\sin \alpha  = \cos \beta ;\cos \alpha  = \sin \beta ;\tan \alpha  = \cot \beta ;\cot \alpha  = \tan \beta. \)

    Nếu hai góc nhọn \(\alpha \) và \(\beta \) có \(\sin \alpha  = \sin \beta \) hoặc \(\cos \alpha  = \cos \beta \) thì \(\alpha  = \beta \)

    So sánh các tỉ số lượng giác

    Với \(\alpha ;\beta \)  là hai góc nhọn bất kì và \(\alpha  < \beta \) thì

    \(\sin \alpha  < \sin \beta ;\,\cos \alpha  > \cos \beta ;\tan \alpha  < \tan \beta ;\cot \alpha  > \cot \beta .\)

    3. Bảng tỉ số lượng giác các góc đặc biệt

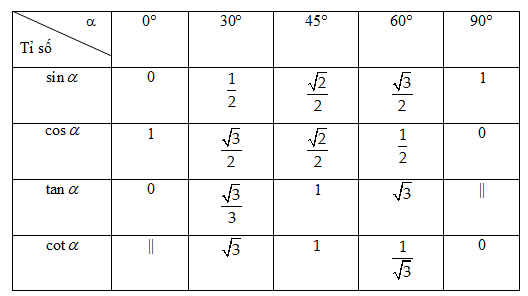
    4. Hệ thức về cạnh và góc trong tam giác vuông

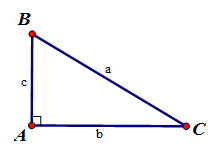
    Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Ta có :

    \(b = a.\sin B = a.\cos C\); \(c = a.\sin C = a.\cos B\); \(b = c.\tan B = c.\cot C\); \(c = b.\tan C = b.\cot B.\)

    Trong một tam giác vuông

    +) Cạnh  góc vuông  = (cạnh huyền ) x (sin góc đối)  = (cạnh huyền ) x (cosin góc kề)

    +) Cạnh  góc vuông  = (cạnh góc vuông ) x (tan  góc đối)  = (cạnh góc vuông còn lại ) x (cotan  góc kề).

    Xem toàn bộ nội dung Toán 9:

    (381) 1269 24/09/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 9 Toán 9