Hàm số bậc nhất

Lý thuyết về hàm số bậc nhất đưa ra định nghĩa và tính chất của hàm số bậc nhất cùng phương pháp giải các dạng toán thường gặp Toán 9
(390) 1300 24/09/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Sơ đồ tư duy Hàm số bậc nhất

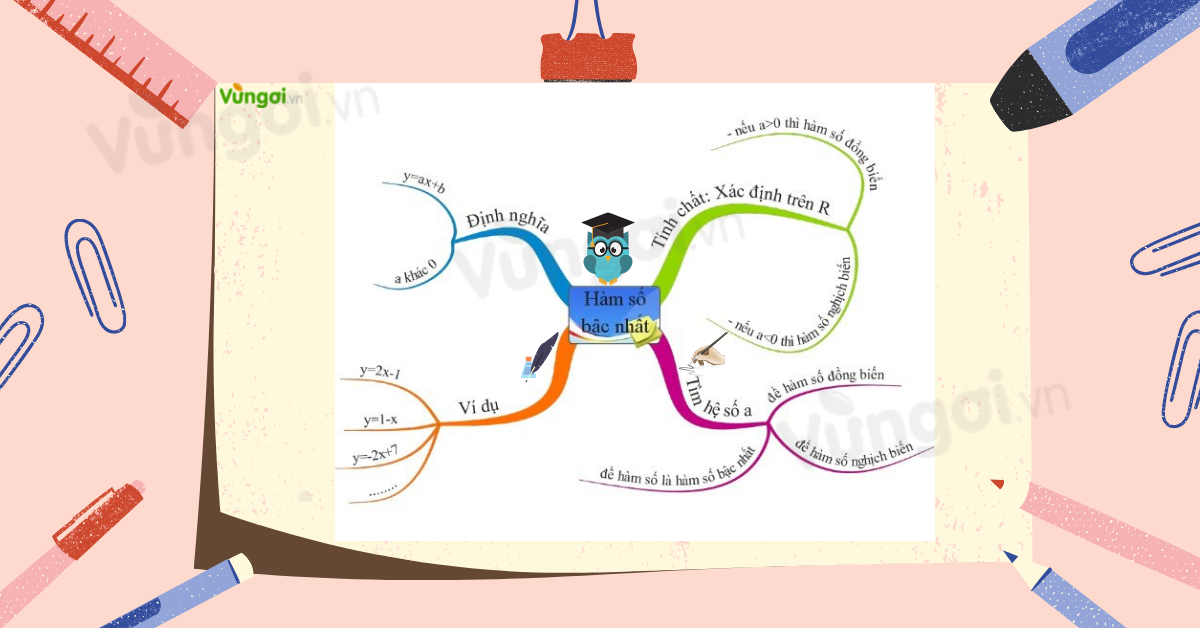
    II. Hàm số bậc nhất

    1. Các kiến thức cần nhớ

    Định nghĩa hàm số bậc nhất

    Hàm số bậc nhất là hàm số được cho bởi công thức $y = ax + b$ trong đó $a,b$ là các số cho trước và $a \ne 0$.

    Khi $b = 0$ hàm số có dạng $y = ax$.

    Tính chất

    Hàm số bậc nhất $y = ax + b$ xác định với mọi giá trị của $x$ thuộc \(\mathbb{R}\) và có tính chất sau

    - Đồng biến trên \(\mathbb{R}\) nếu \(a > 0\).

    - Nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\).

    2. Các dạng toán thường gặp

    Dạng 1: Nhận dạng hàm số bậc nhất

    Phương pháp:

    Hàm số bậc nhất là hàm số có dạng $y = ax + b\,\,\left( {a \ne 0} \right)$.

    Dạng 2: Tìm $m$ để hàm số đồng biến, nghịch biến

    Phương pháp:

    Ta có hàm số bậc nhất $y = ax + b,\,\left( {a \ne 0} \right)$

    - Đồng biến trên \(\mathbb{R}\) nếu \(a > 0\).

    - Nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\).

    Xem toàn bộ nội dung Toán 9:

    (390) 1300 24/09/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 9 Toán 9