Phương pháp giải các bài tập đường thẳng vuông góc với mặt phẳng

Phương pháp giải các bài toán đường thẳng vuông góc với mặt phẳng MÔN TOÁN Lớp 11 kèm bài tập vận dụng
(387) 1290 29/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    Dưới đây là một số bài toán về quan hệ vuông góc trong không gian:

    Dạng 1: Chứng minh đường thẳng vuông góc với mặt phẳng

    Phương pháp:

    Muốn chứng minh đường thẳng $d \bot \left( \alpha  \right)$ ta có thể dùng một trong ba cách sau.

    Cách 1. Chứng minh $d$ vuông góc với hai đường thẳng $a,b$ cắt nhau trong $\left( \alpha  \right)$.

    Kí hiệu: $\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \subset \left( \alpha  \right),b \subset \left( \alpha  \right)\\a \cap b = I\end{array} \right. \Rightarrow a \bot \left( \alpha  \right)$

    Cách 2. Chứng minh $d$ song song với đường thẳng $a$ mà $a$ vuông góc với $\left( \alpha  \right)$.

    Kí hiệu: $\left\{ \begin{array}{l}d\parallel a\\\left( \alpha  \right) \bot a\end{array} \right. \Rightarrow d \bot \left( \alpha  \right)$

    Cách 3. Chứng minh $d$ vuông góc với $\left( Q \right)$ và $\left( Q \right)//\left( P \right)$.

    Dạng 2: Chứng minh hai đường thẳng vuông góc bằng cách dùng đường thẳng vuông góc mặt phẳng

    Phương pháp:

    Để chứng minh $d \bot \;a$, ta có thể chứng minh bởi một trong các cách sau:

    Cách 1: Chứng minh $d$ vuông góc với $\left( P \right)$ và $\left( P \right)$ chứa $a$.

    Cách 2: Sử dụng định lí ba đường vuông góc.

    Cách 3: Sử dụng các cách chứng minh đã biết ở phần trước.

    Ví dụ:

    Cho tứ diện \(SABC\) có tam giác \(ABC\) vuông tại \(B\), \(SA \bot \left( {ABC} \right)\)

    a) Chứng minh: \(BC \bot \left( {SAB} \right)\)

    b) Gọi \(AH\) là đường cao của \(\Delta SAB\). Chứng minh: \(AH \bot SC\)

    Giải

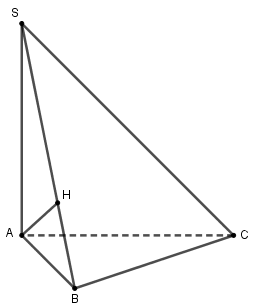
    a) Ta có: \(\left\{ \begin{array}{l}SA \bot \left( {ABC} \right)\\BC \subset \left( {ABC} \right)\end{array} \right. \Rightarrow SA \bot BC\)

    Mà \(BC \bot AB\) (do tam giác \(ABC\) vuông tại \(B\))

    Nên \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\) (đpcm)

    b) Do \(\left\{ \begin{array}{l}BC \bot \left( {SAB} \right)\\AH \subset \left( {SAB} \right)\end{array} \right. \Rightarrow BC \bot AH\) (1)

    Lại có \(AH \bot SB\) (2)

    Từ (1) và (2) suy ra \(AH \bot \left( {SBC} \right)\)

    Mà \(SC \subset \left( {SBC} \right) \Rightarrow AH \bot SC\) (đpcm).

    Xem toàn bộ nội dung Toán 11:

    (387) 1290 29/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 11 Toán 11