Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiXét hệ phương trình \(\left\{ \begin{array}{l}{2^x} - {2^y} = y - x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} + xy + {y^2} = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)có nghiệm \(\left( {x;y} \right)\). Khi đó phát biểu nào sau đây đúng:
A.
\({x^2} + {y^2} = 2\)
B.
\(x - y = 2\)
C.
\(x + y = 2\)
D.
\(xy = 2\)
Lời giải của giáo viên
ToanVN.com
Đáp án đúng: a
Ta có: \(\left( 1 \right) \Leftrightarrow {2^x} + x = {2^y} + y\,\,\,\,\,\,\,\,\left( * \right)\)
Xét hàm số \(f\left( t \right) = {2^t} + t\) trên \(\mathbb{R},\) ta có: \(f'\left( t \right) = {2^t}\ln 2 + 1 > 0,\,\forall t \in \mathbb{R}.\)
Vậy hàm số \(f\left( t \right)\) đồng biến trên \(\mathbb{R}.\)
Do đó: \(\left( * \right) \Leftrightarrow f\left( x \right) = f\left( y \right) \Leftrightarrow x = y.\)
Thay \(x = y\) vào (2) ta được: \(3{x^2} = 3 \Leftrightarrow {x^2} = 1 \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = 1\\x = - 1 \Rightarrow y = - 1\end{array} \right. \Rightarrow \left( {x;y} \right) = \left( {1;1} \right),\left( { - 1; - 1} \right).\)
Hướng dẫn giải:
Biến đổi phương trình \(\left( 1 \right)\) về dạng đặc biệt rồi dùng hàm đặc trưng giải phương trình.
Ta có: \(\left( 1 \right) \Leftrightarrow {2^x} + x = {2^y} + y\,\,\,\,\,\,\,\,\left( * \right)\)
Xét hàm số \(f\left( t \right) = {2^t} + t\) trên \(\mathbb{R},\) ta có: \(f'\left( t \right) = {2^t}\ln 2 + 1 > 0,\,\forall t \in \mathbb{R}.\)
Vậy hàm số \(f\left( t \right)\) đồng biến trên \(\mathbb{R}.\)
Do đó: \(\left( * \right) \Leftrightarrow f\left( x \right) = f\left( y \right) \Leftrightarrow x = y.\)
Thay \(x = y\) vào (2) ta được: \(3{x^2} = 3 \Leftrightarrow {x^2} = 1 \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = 1\\x = - 1 \Rightarrow y = - 1\end{array} \right. \Rightarrow \left( {x;y} \right) = \left( {1;1} \right),\left( { - 1; - 1} \right).\)
Hướng dẫn giải:
Biến đổi phương trình \(\left( 1 \right)\) về dạng đặc biệt rồi dùng hàm đặc trưng giải phương trình.
CÂU HỎI CÙNG CHỦ ĐỀ
Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).
Một người mua xe máy với giá 45 triệu đồng. Biết rằng giá trị khấu hao tài sản xe giảm 60% mỗi năm. Hỏi sau bao nhiêu năm thì giá trị xe chỉ còn 5 triệu đồng?
Với \(a,\,b\) là các số thực dương bất kì, \({\log _2}\dfrac{a}{{{b^2}}}\) bằng:
Tập xác định của hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) là:
Cho \(x;y\) là hai số thực dương thỏa mãn \(x \ne y\) và \({\left( {{2^x} + \dfrac{1}{{{2^x}}}} \right)^y} < {\left( {{2^y} + \dfrac{1}{{{2^y}}}} \right)^x}.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\).
Tính tổng \(T\) tất cả các nghiệm của phương trình \({\left( {x - 3} \right)^{2{x^2} - 5x}} = 1\).
Tìm số các giá trị nguyên không dương của tham số \(m\) để hàm số \(y = \dfrac{{m\ln x - 2}}{{\ln x + m - 3}}\) đồng biến trên \(\left( {{e^2}; + \infty } \right)\) là
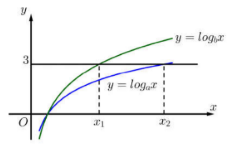
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:
Giá trị của $x$ thỏa mãn \({\log _{\frac{1}{2}}}(3 - x) = 2\) là
Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?
Tìm tập nghiệm $S$ của bất phương trình ${\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}(x) > {\log _2}({x^2} - x) - 1$
Cho hệ phương trình \(\left\{ \begin{array}{l}{\left( {\dfrac{2}{3}} \right)^{2x - y}} + 6{\left( {\dfrac{2}{3}} \right)^{\dfrac{{2x - y}}{2}}} - 7 = 0\\{3^{{{\log }_9}\left( {x - y} \right)}} = 1\end{array} \right.\). Chọn khẳng định đúng?
