Cho các số \(a,\ b,\ c\) và \(a,\ c\ne 1\). Khẳng định nào sau đây đúng?
A.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{b}}c\)
B.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{a}}\left( \frac{b}{c} \right)\)
C.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{c}}b\)
D.
\(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}={{\log }_{a}}\left( b-c \right)\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
Ta có: \(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}=\frac{{{\log }_{a}}c.{{\log }_{c}}b}{{{\log }_{a}}c}={{\log }_{c}}b.\)
Hướng dẫn giải:
Áp dụng các công thức cơ bản của hàm số logarit: \({{\log }_{a}}c={{\log }_{a}}b.{{\log }_{b}}c.\)
Ta có: \(\frac{{{\log }_{a}}b}{{{\log }_{a}}c}=\frac{{{\log }_{a}}c.{{\log }_{c}}b}{{{\log }_{a}}c}={{\log }_{c}}b.\)
Hướng dẫn giải:
Áp dụng các công thức cơ bản của hàm số logarit: \({{\log }_{a}}c={{\log }_{a}}b.{{\log }_{b}}c.\)
CÂU HỎI CÙNG CHỦ ĐỀ
Một người mua xe máy với giá 45 triệu đồng. Biết rằng giá trị khấu hao tài sản xe giảm 60% mỗi năm. Hỏi sau bao nhiêu năm thì giá trị xe chỉ còn 5 triệu đồng?
Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).
Cho \(x;y\) là hai số thực dương thỏa mãn \(x \ne y\) và \({\left( {{2^x} + \dfrac{1}{{{2^x}}}} \right)^y} < {\left( {{2^y} + \dfrac{1}{{{2^y}}}} \right)^x}.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\).
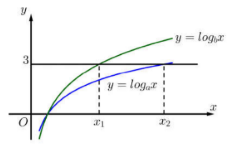
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:
Công thức nào sau đây là công thức tăng trưởng mũ?
Tính tổng \(T\) tất cả các nghiệm của phương trình \({\left( {x - 3} \right)^{2{x^2} - 5x}} = 1\).
Với \(a,\,b\) là các số thực dương bất kì, \({\log _2}\dfrac{a}{{{b^2}}}\) bằng:
Tập xác định của hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) là:
Giá trị của $x$ thỏa mãn \({\log _{\frac{1}{2}}}(3 - x) = 2\) là
Tìm số các giá trị nguyên không dương của tham số \(m\) để hàm số \(y = \dfrac{{m\ln x - 2}}{{\ln x + m - 3}}\) đồng biến trên \(\left( {{e^2}; + \infty } \right)\) là
Tìm tập nghiệm $S$ của bất phương trình ${\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}(x) > {\log _2}({x^2} - x) - 1$
Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?
Xét hệ phương trình \(\left\{ \begin{array}{l}{2^x} - {2^y} = y - x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} + xy + {y^2} = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)có nghiệm \(\left( {x;y} \right)\). Khi đó phát biểu nào sau đây đúng:

