Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiCho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác cân \(AB = AC = a;\widehat {BAC} = {120^0}\) và $AB'$ vuông góc với $\left( {A'B'C'} \right)$ . Mặt phẳng $\left( {AA'C'} \right)$ tạo với mặt phẳng $\left( {A'B'C'} \right)$ một góc \({30^0}\). Thể tích khối lăng trụ $ABC.A'B'C'$ là:
A.
\(\dfrac{{{a^3}\sqrt 3 }}{3}\)
B.
\(\dfrac{{8{a^3}}}{3}\)
C.
\(\dfrac{{{a^3}\sqrt 3 }}{8}\)
D.
\(\dfrac{{{a^3}\sqrt 3 }}{2}\)
Lời giải của giáo viên
ToanVN.com
Đáp án đúng: c
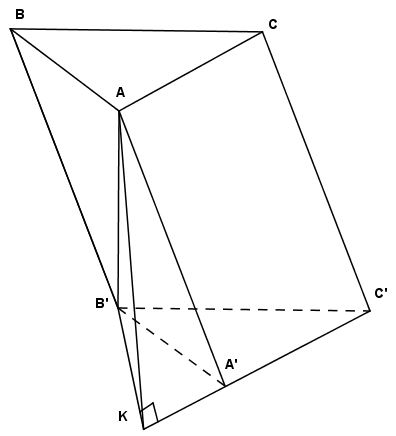
Trong (A’B’C’) kẻ \(B'K \bot A'C'\,\,\left( {K \in A'C'} \right)\)
Ta có:
\(\left. \begin{array}{l}AB' \bot A'C'\left( {AB' \bot \left( {A'B'C'} \right)} \right)\\B'K \bot A'C'\end{array} \right\} \Rightarrow A'C' \bot \left( {AB'K} \right) \Rightarrow A'C' \bot AK\)
\(\left. \begin{array}{l}\left( {AA'C'} \right) \cap \left( {A'B'C'} \right) = A'C'\\\left( {AA'C'} \right) \supset AK \bot A'C'\\\left( {A'B'C'} \right) \supset B'K \bot A'C'\end{array} \right\} \Rightarrow \widehat {\left( {\left( {AA'C'} \right);\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AK;B'K} \right)} = \widehat {AKB'} = {30^0}\)
Ta có:
\(\begin{array}{l}{S_{A'B'C'}} = \dfrac{1}{2}A'B'.A'C'.\sin 120 = \dfrac{1}{2}{a^2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{1}{2}B'K.A'C'\\ \Rightarrow B'K = \dfrac{{2{S_{A'B'C'}}}}{{A'C'}} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{2}}}{a} = \dfrac{{a\sqrt 3 }}{2}\end{array}\)
\(AB' \bot \left( {A'B'C'} \right) \Rightarrow AB' \bot B'K \Rightarrow \Delta AB'K\) vuông tại B’
$ \Rightarrow AB' = B'K.tan30 = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{3} = \dfrac{a}{2}$
Vậy \({V_{ABC.A'B'C'}} = AB'.{S_{A'B'C'}} = \dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\)
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng cùng vuông góc với giao tuyến.
- Tính diện tích đáy \({S_{A'B'C'}}\) và đường cao \(AB'\).
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
Trong (A’B’C’) kẻ \(B'K \bot A'C'\,\,\left( {K \in A'C'} \right)\)
Ta có:
\(\left. \begin{array}{l}AB' \bot A'C'\left( {AB' \bot \left( {A'B'C'} \right)} \right)\\B'K \bot A'C'\end{array} \right\} \Rightarrow A'C' \bot \left( {AB'K} \right) \Rightarrow A'C' \bot AK\)
\(\left. \begin{array}{l}\left( {AA'C'} \right) \cap \left( {A'B'C'} \right) = A'C'\\\left( {AA'C'} \right) \supset AK \bot A'C'\\\left( {A'B'C'} \right) \supset B'K \bot A'C'\end{array} \right\} \Rightarrow \widehat {\left( {\left( {AA'C'} \right);\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AK;B'K} \right)} = \widehat {AKB'} = {30^0}\)
Ta có:
\(\begin{array}{l}{S_{A'B'C'}} = \dfrac{1}{2}A'B'.A'C'.\sin 120 = \dfrac{1}{2}{a^2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{1}{2}B'K.A'C'\\ \Rightarrow B'K = \dfrac{{2{S_{A'B'C'}}}}{{A'C'}} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{2}}}{a} = \dfrac{{a\sqrt 3 }}{2}\end{array}\)
\(AB' \bot \left( {A'B'C'} \right) \Rightarrow AB' \bot B'K \Rightarrow \Delta AB'K\) vuông tại B’
$ \Rightarrow AB' = B'K.tan30 = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{3} = \dfrac{a}{2}$
Vậy \({V_{ABC.A'B'C'}} = AB'.{S_{A'B'C'}} = \dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\)
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng cùng vuông góc với giao tuyến.
- Tính diện tích đáy \({S_{A'B'C'}}\) và đường cao \(AB'\).
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
CÂU HỎI CÙNG CHỦ ĐỀ
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:
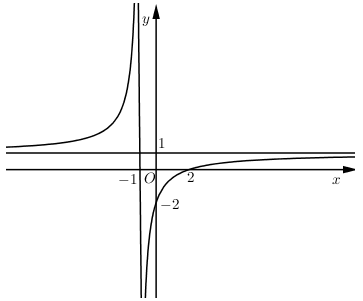
Cho hàm số \(y = \dfrac{{2x - 2}}{{x - 2}}\) có đồ thị là\(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\)thỏa mãn bài toán. Tìm giá trị của \(S\).
Tìm TXĐ của hàm số \(y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}\)
Tập hợp nghiệm của phương trình \({\log _3}\left( {{9^{50}} + 6{x^2}} \right) = {\log _{\sqrt 3 }}\left( {{3^{50}} + 2x} \right)\) là:
Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).
Tìm giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
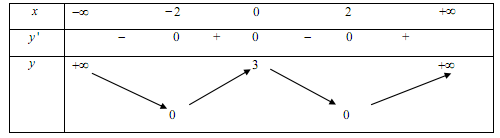
Khẳng định nào sau đây là khẳng định đúng?
Cho hàm số \(y = {3^x} + \ln 3\). Chọn mệnh đề đúng:
Đơn giản biểu thức $P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right)\,\,\,\,(a,b > 0)$ ta được:
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
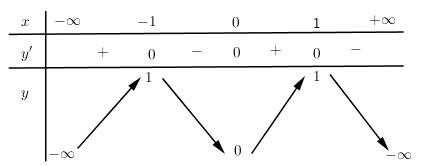
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Nếu $\log_a b{\rm{ }} = {\rm{ }}p$ thì $\log_a{a^2}{b^4}$ bằng:
Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:
