Cho hàm số \(y = \dfrac{{2x - 2}}{{x - 2}}\) có đồ thị là\(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\)thỏa mãn bài toán. Tìm giá trị của \(S\).
A.
\(6\)
B.
\(5\)
C.
\(8\)
D.
\(7\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\). Đồ thị hàm số có hai đường tiệm cận là \(x = 2\) và \(y = 2\).
Ta có \(y' = \dfrac{{ - 2}}{{{{\left( {x - 2} \right)}^2}}}\). Gọi \(M\left( {m;\,\dfrac{{2m - 2}}{{m - 2}}} \right)\) thuộc đồ thị hàm số.
Phương trình tiếp tuyến \(d\) của \(\left( C \right)\) tại \(M\): \(y = \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {x - m} \right) + \dfrac{{2m - 2}}{{m - 2}}\).
Cho \(x = 2 \Rightarrow y = \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {2 - m} \right) + \dfrac{{2m - 2}}{{m - 2}}\)\( \Leftrightarrow y = \dfrac{2}{{m - 2}} + \dfrac{{2m - 2}}{{m - 2}} = \dfrac{{2m}}{{m - 2}}\).
\( \Rightarrow \) Giao điểm của \(d\) và đường thẳng \(x = 2\) là \(A\left( {2;\,\dfrac{{2m}}{{m - 2}}} \right)\).
Cho \(y = 2 \Rightarrow \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {x - m} \right) + \dfrac{{2m - 2}}{{m - 2}} = 2\).
\(\begin{array}{l} \Leftrightarrow - 2\left( {x - m} \right) + \left( {2m - 2} \right)\left( {m - 2} \right) = 2{\left( {m - 2} \right)^2}\\ \Leftrightarrow - 2x + 2m + 2{m^2} - 6m + 4 = 2{m^2} - 8m + 8\\ \Leftrightarrow 2x = 4m - 4 \Leftrightarrow x = 2m - 2\end{array}\)
\( \Rightarrow \) Giao điểm của \(d\) và đường thẳng \(y = 2\) là \(B\left( {2m - 2;\,2} \right)\).
Ta có: \(AB = 2\sqrt 5 \Leftrightarrow {\left( {2m - 4} \right)^2} + {\left( {2 - \dfrac{{2m}}{{m - 2}}} \right)^2} = 20\)
\(\begin{array}{l} \Leftrightarrow 4{\left( {m - 2} \right)^2} + \dfrac{{16}}{{{{\left( {m - 2} \right)}^2}}} = 20\\ \Leftrightarrow {\left( {m - 2} \right)^4} - 5{\left( {m - 2} \right)^2} + 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{\left( {m - 2} \right)^2} = 1\\{\left( {m - 2} \right)^2} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = 1\\m = 4\\m = 0\end{array} \right.\end{array}\)
Vậy \(S = 3 + 1 + 4 + 0 = 8\).
Hướng dẫn giải:
- Tìm 2 đường tiệm cận của đồ thị hàm số.
- Gọi \(M\left( {m;\,\dfrac{{2m - 2}}{{m - 2}}} \right)\) thuộc đồ thị hàm số. Viết phương trình tiếp tuyến của đồ thị hàm số tại \(M\).
- Tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).
- Tìm giao điểm \(A,\,\,B\) của tiếp tuyến với 2 đường tiệm cận.
- Tính độ dài đoạn thẳng \(AB:\) \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).
- Giải phương trình tìm \(m\), từ đó tính \(S\).
TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\). Đồ thị hàm số có hai đường tiệm cận là \(x = 2\) và \(y = 2\).
Ta có \(y' = \dfrac{{ - 2}}{{{{\left( {x - 2} \right)}^2}}}\). Gọi \(M\left( {m;\,\dfrac{{2m - 2}}{{m - 2}}} \right)\) thuộc đồ thị hàm số.
Phương trình tiếp tuyến \(d\) của \(\left( C \right)\) tại \(M\): \(y = \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {x - m} \right) + \dfrac{{2m - 2}}{{m - 2}}\).
Cho \(x = 2 \Rightarrow y = \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {2 - m} \right) + \dfrac{{2m - 2}}{{m - 2}}\)\( \Leftrightarrow y = \dfrac{2}{{m - 2}} + \dfrac{{2m - 2}}{{m - 2}} = \dfrac{{2m}}{{m - 2}}\).
\( \Rightarrow \) Giao điểm của \(d\) và đường thẳng \(x = 2\) là \(A\left( {2;\,\dfrac{{2m}}{{m - 2}}} \right)\).
Cho \(y = 2 \Rightarrow \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {x - m} \right) + \dfrac{{2m - 2}}{{m - 2}} = 2\).
\(\begin{array}{l} \Leftrightarrow - 2\left( {x - m} \right) + \left( {2m - 2} \right)\left( {m - 2} \right) = 2{\left( {m - 2} \right)^2}\\ \Leftrightarrow - 2x + 2m + 2{m^2} - 6m + 4 = 2{m^2} - 8m + 8\\ \Leftrightarrow 2x = 4m - 4 \Leftrightarrow x = 2m - 2\end{array}\)
\( \Rightarrow \) Giao điểm của \(d\) và đường thẳng \(y = 2\) là \(B\left( {2m - 2;\,2} \right)\).
Ta có: \(AB = 2\sqrt 5 \Leftrightarrow {\left( {2m - 4} \right)^2} + {\left( {2 - \dfrac{{2m}}{{m - 2}}} \right)^2} = 20\)
\(\begin{array}{l} \Leftrightarrow 4{\left( {m - 2} \right)^2} + \dfrac{{16}}{{{{\left( {m - 2} \right)}^2}}} = 20\\ \Leftrightarrow {\left( {m - 2} \right)^4} - 5{\left( {m - 2} \right)^2} + 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{\left( {m - 2} \right)^2} = 1\\{\left( {m - 2} \right)^2} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = 1\\m = 4\\m = 0\end{array} \right.\end{array}\)
Vậy \(S = 3 + 1 + 4 + 0 = 8\).
Hướng dẫn giải:
- Tìm 2 đường tiệm cận của đồ thị hàm số.
- Gọi \(M\left( {m;\,\dfrac{{2m - 2}}{{m - 2}}} \right)\) thuộc đồ thị hàm số. Viết phương trình tiếp tuyến của đồ thị hàm số tại \(M\).
- Tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).
- Tìm giao điểm \(A,\,\,B\) của tiếp tuyến với 2 đường tiệm cận.
- Tính độ dài đoạn thẳng \(AB:\) \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).
- Giải phương trình tìm \(m\), từ đó tính \(S\).
CÂU HỎI CÙNG CHỦ ĐỀ
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:

Tìm TXĐ của hàm số \(y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}\)
Tìm giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$
Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).
Tập hợp nghiệm của phương trình \({\log _3}\left( {{9^{50}} + 6{x^2}} \right) = {\log _{\sqrt 3 }}\left( {{3^{50}} + 2x} \right)\) là:
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
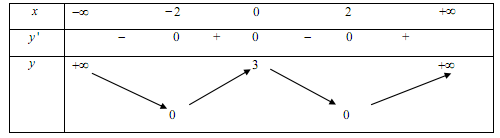
Khẳng định nào sau đây là khẳng định đúng?
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
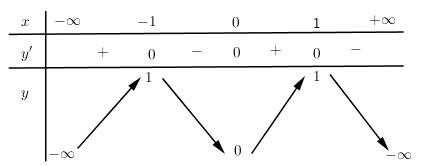
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Cho hàm số $y = {x^4} - 4{x^2} + 3$. Tìm tất cả các giá trị của tham số $m$ sao cho phương trình $\left| {{x^4} - 4{x^2} + 3} \right| = m$ có $4$ nghiệm phân biệt.
Đơn giản biểu thức $P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right)\,\,\,\,(a,b > 0)$ ta được:
Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:
Khi quay hình chữ nhật \(MNPQ\) quanh đường thẳng \(AB\) với \(A,B\) lần lượt là trung điểm của \(MN,PQ\) ta được một hình trụ có đường kính đáy:
Cho $x, y$ là các số thực thỏa mãn \({\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của biểu thức \(P = 2x - y\).
Cho hàm số \(y = {3^x} + \ln 3\). Chọn mệnh đề đúng:

