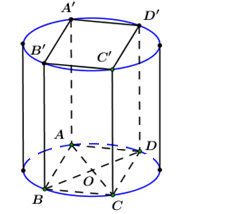
Ta có hình hộp \(ABCD.A'B'C'D'\) có các cạnh bằng \(a\)

\( \Rightarrow AA' = a\) là đường sinh của hình trụ.

Bán kính đáy của hình trụ là \(R = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}.\)

\( \Rightarrow \) Diện tích xung quanh của hình trụ là:

\({S_{xq}} = 2\pi Rl = 2\pi .\dfrac{{a\sqrt 2 }}{2}.a = \sqrt 2 \pi {a^2}.\)  

Áp dụng công thức \({S_{xq}} = \pi rl\) ta được: \({S_{xq}} = \pi .3.4 = 12\pi \left( {c{m^2}} \right)\)

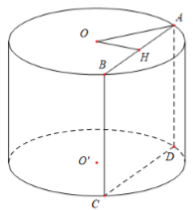
Giả sử thiết diện là hình chữ nhật \(ABCD\).

Ta có: \({S_{ABCD}} = AB.BC \Rightarrow 20{a^2} = AB.5a \Leftrightarrow AB = 4a\) \( \Rightarrow AH = 2a\).

Gọi \(O,\,\,O'\) lần lượt là tâm hai đáy của hình trụ, \(H\) là trung điểm của \(AB\).

Ta có \(\left\{ \begin{array}{l}OH \bot AB\\OH \bot BC\end{array} \right. \Rightarrow OH \bot \left( {ABCD} \right) \Rightarrow OH = 3a\).

Áp dụng định lí Pytago trong tam giác vuông \(OAH\) ta có: \(OA = \sqrt {O{H^2} + A{H^2}}  = \sqrt {9{a^2} + 4{a^2}}  = a\sqrt {13} \).

Vậy thể tích khối trụ là \(V = \pi .O{A^2}.BC = \pi .{\left( {a\sqrt {13} } \right)^2}.5a = 65\pi {a^3}\).

Mặt cầu \(\left( S \right)\) có đường kính là 10cm  bán kính \(R = 5cm\).

Mà khoảng cách từ tâm của mặt cầu và mặt phẳng \(\left( P \right)\) là \(d = 4cm < R\).

Do đó mặt phẳng \(\left( P \right)\) cắt \(\left( S \right)\) theo một đường tròn có bán kính \(r = \sqrt {{R^2} - {d^2}}  = 3\,\,\left( {cm} \right)\).

Vậy trong 4 đáp án chỉ có đáp án C sai.

Nếu \(\left( P \right)\) là mặt phẳng kính thì \(OH = 0\left( {H \equiv O} \right)\) hay \(\left( P \right)\) đi qua \(O\) là tâm mặt cầu.

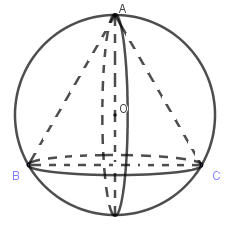
Quan sát hình vẽ ta thấy, khi quay hình \(\left( H \right)\) quanh trục đối xứng ta được hình nón nội tiếp hình cầu.

Đường thẳng và mặt cầu chỉ có thể có số giao điểm là \(0;1;2\) nên số giao điểm lớn nhất có thể có là \(2\) giao điểm.

Đường thẳng đi qua tâm và vuông góc với mặt phẳng chứa đường tròn được gọi là trục đường tròn.

Gọi mặt phẳng đi qua đỉnh của hình nón là \(\left( {SMN} \right)\).

Do thiết diện của \(\left( {SMN} \right)\) và hình nón là tam giác đều cạnh \(2a\) nên \(SM = MN = SN = 2a\)

Kẻ \(OH \bot AB\). Nối \(S\) với \(H.\)

Khi đó \(H\) là trung điểm \(MN\) nên \(SH = a\sqrt 3 \)

Ta có: góc giữa \(\left( {SMN} \right)\) và mặt đáy là \(\angle SHO\)

Trong tam giác \(SHO\) vuông tại \(O\) ta có: \(\tan SHO = \dfrac{{SO}}{{OH}}\)\( \Rightarrow \tan {30^o} = \dfrac{{SO}}{{OH}} \Rightarrow SO = \dfrac{{\sqrt 3 }}{3}.OH\)

Theo định lí py-ta-go ta có: \(S{O^2} + O{H^2} = S{H^2}\)\( \Rightarrow \dfrac{4}{3}O{H^2} = S{H^2} \Rightarrow OH = \dfrac{{\sqrt 3 }}{2}SH = \dfrac{{3a}}{2}\)

\( \Rightarrow SO = \dfrac{{\sqrt 3 }}{2}a\)\( \Rightarrow OM = \sqrt {S{M^2} - S{O^2}}  = \sqrt {4{a^2} - \dfrac{{3{a^2}}}{4}}  = \dfrac{{a\sqrt {13} }}{2}\)

Diện tích xung quanh của hình nón: \({S_{xq}} = \pi .\dfrac{{a\sqrt {13} }}{2}.2a = \pi \sqrt {13} {a^2}\)

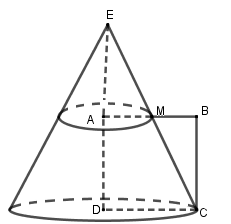
Kéo dài \(CM\) cắt \(DA\) tại \(E\). Quay hình thang vuông \(AMCD\) quanh trục \(AD\) ta được hình nón cụt như hình vẽ.

Quay tam giác \(EDC\) quanh trục \(ED\) ta được hình nón.

Dễ thấy \({V_{nc}} = {V_1} - {V_2}\), ở đó \({V_1}\) là thể tích khối nón đỉnh \(E\), bán kính đáy \(DC = 2\) và \({V_2}\) là thể tích khối nón đỉnh \(E\), bán kính đáy \(AM = 1\).

Có \(\dfrac{{EA}}{{ED}} = \dfrac{{AM}}{{DC}} = \dfrac{1}{2} \Rightarrow EA = AD = 2 \Rightarrow ED = 4\)

\( \Rightarrow {V_1} = \dfrac{1}{3}\pi D{C^2}.ED = \dfrac{1}{3}\pi {.2^2}.4 = \dfrac{{16\pi }}{3}\) ;

\({V_2} = \dfrac{1}{3}\pi A{M^2}EA = \dfrac{1}{3}\pi {.1^2}.2 = \dfrac{{2\pi }}{3}\).

Vậy \(V = {V_1} - {V_2} = \dfrac{{16\pi }}{3} - \dfrac{{2\pi }}{3} = \dfrac{{14\pi }}{3}\).

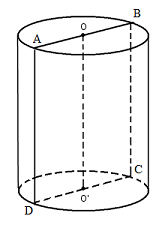
Gọi \(R,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ.

Giả sử thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật \(ABCD\) như hình vẽ, ta có \(AB = 2R\) và \(AD = h\).

Chu vi thiết diện chứa trục bằng 12 \( \Rightarrow 2R + h = 6 \Rightarrow h = 6 - 2R\).

Khi đó thể tích khối trụ:

\(\begin{array}{l}V = \pi {R^2}h = \pi {R^2}\left( {6 - 2R} \right) = \pi .R.R\left( {6 - 2R} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \le \pi .{\left( {\dfrac{{R + R + 6 - 2R}}{3}} \right)^3} = 8\pi \end{array}\)

Dấu “=” xảy ra khi và chỉ khi \(R = 6 - 2R \Leftrightarrow R = 2.\)

Vậy thể tích khối trụ lớn nhất là \(8\pi \) khi \(R = 2\).

Thể tích gáo \({V_1} = \pi {R^2}.h = \pi .0,{04^2}.0,05 = 8\pi {.10^{ - 5}}({m^3})\)

Số nước múc ra trong một ngày \({V_2} = 170{V_1} = 170.8.\pi {.10^{ - 5}} = 0,0136\pi \left( {{m^3}} \right)\)

Số ngày dùng hết nước là \(\dfrac{{2.3.2}}{{{V_2}}} = \dfrac{{12}}{{0,0136\pi }} \approx 281\)(ngày)