Cho hình trụ có chiều cao bằng \(5a\), cắt hình trụ bởi mặt phẳng song song với trục và cách trục một khoảng bằng \(3a\) được thiết diện có diện tích bằng \(20{a^2}\). Thể tích khối trụ là:
A.
\(5\pi {a^3}\)
B.
\(125\pi {a^3}\)
C.
\(65\pi {a^3}\)
D.
\(\dfrac{{65\pi {a^3}}}{3}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
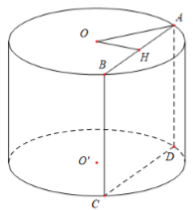
Giả sử thiết diện là hình chữ nhật \(ABCD\).
Ta có: \({S_{ABCD}} = AB.BC \Rightarrow 20{a^2} = AB.5a \Leftrightarrow AB = 4a\) \( \Rightarrow AH = 2a\).
Gọi \(O,\,\,O'\) lần lượt là tâm hai đáy của hình trụ, \(H\) là trung điểm của \(AB\).
Ta có \(\left\{ \begin{array}{l}OH \bot AB\\OH \bot BC\end{array} \right. \Rightarrow OH \bot \left( {ABCD} \right) \Rightarrow OH = 3a\).
Áp dụng định lí Pytago trong tam giác vuông \(OAH\) ta có: \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {9{a^2} + 4{a^2}} = a\sqrt {13} \).
Vậy thể tích khối trụ là \(V = \pi .O{A^2}.BC = \pi .{\left( {a\sqrt {13} } \right)^2}.5a = 65\pi {a^3}\).
Hướng dẫn giải:
- Sử dụng định lí Pytago tính bán kính đáy của hình trụ.
- Thể tích khối trụ có chiều cao \(h\), bán kính đáy \(R\) là \(V = \pi {R^2}h\).

Giả sử thiết diện là hình chữ nhật \(ABCD\).
Ta có: \({S_{ABCD}} = AB.BC \Rightarrow 20{a^2} = AB.5a \Leftrightarrow AB = 4a\) \( \Rightarrow AH = 2a\).
Gọi \(O,\,\,O'\) lần lượt là tâm hai đáy của hình trụ, \(H\) là trung điểm của \(AB\).
Ta có \(\left\{ \begin{array}{l}OH \bot AB\\OH \bot BC\end{array} \right. \Rightarrow OH \bot \left( {ABCD} \right) \Rightarrow OH = 3a\).
Áp dụng định lí Pytago trong tam giác vuông \(OAH\) ta có: \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {9{a^2} + 4{a^2}} = a\sqrt {13} \).
Vậy thể tích khối trụ là \(V = \pi .O{A^2}.BC = \pi .{\left( {a\sqrt {13} } \right)^2}.5a = 65\pi {a^3}\).
Hướng dẫn giải:
- Sử dụng định lí Pytago tính bán kính đáy của hình trụ.
- Thể tích khối trụ có chiều cao \(h\), bán kính đáy \(R\) là \(V = \pi {R^2}h\).
CÂU HỎI CÙNG CHỦ ĐỀ
Đường thẳng đi qua tâm và vuông góc với mặt phẳng chứa đường tròn được gọi là:
Đề thi THPT QG – 2021 lần 1– mã 104
Cắt hình nón \(\left( \aleph \right)\) bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng \({30^o}\), ta được thiết diện là tam giác đều cạnh \(2a.\) Diện tích xung quanh của \(\left( \aleph \right)\) bằng
Cho mặt cầu \(\left( S \right)\). Nếu \(\left( P \right)\) là mặt phẳng kính của mặt cầu \(\left( S \right)\) thì:
Cho mặt cầu \(\left( S \right)\) có đường kính 10 cm và mặt phẳng \(\left( P \right)\) cách tâm mặt cầu một khoảng 4 cm. Khẳng định nào sau đây sai?
Cho hình \(\left( H \right)\) bao gồm tam giác \(ABC\) đều nội tiếp đường tròn \(\left( C \right)\). Quay hình \(\left( H \right)\) quanh trục đối xứng của nó ta được:
Diện tích xung quanh hình nón có bán kính đáy \(r = 3cm\) và độ dài đường sinh \(4cm\) là:
Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi bằng 12. Giá trị lớn nhất của thể tích khối trụ bằng
Số giao điểm của đường thẳng và mặt cầu tối đa có thể có là:
Cho một cái bể nước hình hộp chữ nhật có ba kích thước $2m,3m,2m$ lần lượt là chiều dài, chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một cái gáo nước hình trụ có chiều cao là $5cm$ và bán kính đường tròn đáy là $4cm$. Trung bình một ngày được múc ra $170$ gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi sau bao nhiêu ngày thì bể hết nước biết rằng ban đầu bể đầy nước?
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Diện tích xung quanh của hình trụ có đáy là hai hình tròn ngoại tiếp hai hình vuông \(ABCD\) và \(A'B'C'D'\) là:
Cho hình vuông \(ABCD\) cạnh bằng \(2\). Gọi \(M\) là trung điểm \(AB\). Cho tứ giác \(AMCD\) và các điểm trong của nó quay quanh trục \(AD\) ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.

