Đề kiểm tra 1 tiết chương 3: Nguyên hàm - Đề số 3
-
Hocon247
-
25 câu hỏi
-
45 phút
-
621 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho parabol \(\left( P \right)\) có đồ thị như hình vẽ:

Tính diện tích giới hạn bởi \(\left( P \right)\) và trục hoành.
Ta dễ dàng tìm được phương trình parabol là \(y={{x}^{2}}-4x+3\)
Xét phương trình hoành độ giao điểm \({{x}^{2}}-4x+3=0\Leftrightarrow \left[ \begin{align}x=1 \\x=3 \\\end{align} \right.\)
Khi đó diện tích giới hạn bởi \(\left( P \right)\) và trục hoành là \(S=-\int\limits_{1}^{3}{\left( {{x}^{2}}-4x+3 \right)dx}=\frac{4}{3}\)
Hướng dẫn giải:
Sử dụng công thức ứng dụng tích phân để tính giới hạn của hình phẳng.
Cho hình \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và hai đường thẳng \(x = 0,x = 1\). Thể tích khối tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục \(Ox\) được tính bởi:
Thể tích vật thể là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} = \pi \int\limits_0^1 {{{\left( {{x^3}} \right)}^2}dx} = \pi \int\limits_0^1 {{x^6}dx} \)
Hướng dẫn giải:
Sử dụng công thức tính thể tích khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\) quanh trục \(Ox\): \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án D vì nghĩ \({\left( {{x^3}} \right)^2} = {x^5}\) là sai.
Đổi biến $u = \ln x$ thì tích phân \(I = \int\limits_1^e {\dfrac{{1 - \ln x}}{{{x^2}}}dx} \) thành:
Đặt u = lnx \( \Rightarrow du = \dfrac{{dx}}{x}\) và \(x = {e^u}\).
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow u = 0\\x = e \Rightarrow u = 1\end{array} \right.\)
Khi đó ta có: \(I = \int\limits_1^e {\dfrac{{1 - \ln x}}{{{x^2}}}dx} = \int\limits_0^1 {\dfrac{{1 - u}}{{{e^u}}}du} = \int\limits_0^1 {\left( {1 - u} \right){e^{ - u}}du} \)
Hướng dẫn giải:
- Bước 1: Đặt \(t = u\left( x \right)\), đổi cận \(\left\{ \begin{array}{l}x = a \Rightarrow t = u\left( a \right) = a'\\x = b \Rightarrow t = u\left( b \right) = b'\end{array} \right.\) .
- Bước 2: Tính vi phân \(dt = u'\left( x \right)dx\).
- Bước 3: Biến đổi \(f\left( x \right)dx\) thành \(g\left( t \right)dt\).
- Bước 4: Tính tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_{a'}^{b'} {g\left( t \right)dt} \).
Giải thích thêm:
Một số em sau khi tính được \(I = \int\limits_0^1 {\left( {1 - u} \right){e^{ - u}}du} \) vội vàng kết luận đáp án C mà không chú ý cận.
Đặt \(F\left( x \right) = \int\limits_1^x {\sin tdt} \). Khi đó \(F'\left( x \right)\) là hàm số nào dưới đây?
Ta có: \(F\left( x \right) = \int\limits_1^x {\sin tdt} = \left. { - \cos t} \right|_1^x = - \cos x + \cos 1 \Rightarrow F'\left( x \right) = \sin x\)
Hướng dẫn giải:
Sử dụng công thức tính tích phân \(F\left( b \right) - F\left( a \right) = \int\limits_a^b {f\left( x \right)dx} \).
Giải thích thêm:
HS thường nhầm lẫn \(F'\left( x \right) = \left( { - \cos x + \cos 1} \right)' = \sin x - \sin 1\) và chọn đáp án C là sai.
Hàm số \(F\left( x \right)\) được gọi là nguyên hàm của hàm số \(f\left( x \right)\) nếu:
Hàm số \(F\left( x \right)\) được gọi là nguyên hàm của hàm số \(f\left( x \right)\) nếu \(F'\left( x \right) = f\left( x \right)\).
Giải thích thêm:
HS thường chọn nhầm công thức ở đáp án D vì nhầm lẫn với đạo hàm.
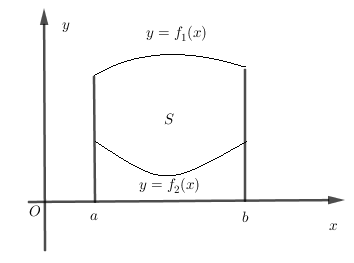
Cho hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và có đồ thị như hình bên. Gọi \(S\) là hình phẳng giới hạn bới hai đồ thị trên và các đường thẳng \(x = a,x = b\). Mệnh đề nào sau đây đúng?
Diện tích hình phẳng giới hạn bởi \(y = {f_1}\left( x \right),y = {f_2}\left( x \right),x = a,x = b\) là: \(S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)
Ta thấy \({f_1}\left( x \right) > {f_2}\left( x \right)\,\,\forall x \in \left( {a;b} \right) \Rightarrow S = \int\limits_a^b {\left( {{f_1}\left( x \right) - {f_2}\left( x \right)} \right)dx} \)
Hướng dẫn giải:
Diện tích hình phẳng giới hạn bởi \(y = {f_1}\left( x \right),y = {f_2}\left( x \right),x = a,x = b\) là: \(S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)
Tính \(I=\int\limits_{0}^{1}{{{e}^{3x}}dx}\).
\(I=\int\limits_{0}^{1}{{{e}^{3x}}dx}=\frac{1}{3}\left. {{e}^{3x}} \right|_{0}^{1}=\frac{{{e}^{3}}-1}{3}\)
Hướng dẫn giải:
Sử dụng công thức \(\int\limits_{{}}^{{}}{{{e}^{kx}}dx}=\frac{1}{k}{{e}^{kx}}+C\)
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Chọn mệnh đề sai?
Các mệnh đề A, B, C đều đúng. Mệnh đề D sai.
Giải thích thêm:
HS thường nhầm lẫn giữa đáp án D và A, cần nhớ kĩ trong khi đổi cận.
Nguyên hàm của hàm số \(f\left( x \right) = \sin x + \cos x\) là :
\(\int\limits_{}^{} {f\left( x \right)dx} = \int\limits_{}^{} {\left( {\sin x + \cos x} \right)dx} = - \cos x + \sin x + C\)
Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \sqrt {{{\ln }^2}x + 1} .\dfrac{{\ln x}}{x}\) thoả mãn \(F\left( 1 \right) = \dfrac{1}{3}\). Giá trị của \({F^2}\left( e \right)\) là
Đặt \(t = \sqrt {{{\ln }^2}x + 1} \Rightarrow tdt = \dfrac{{\ln x}}{x}dx\)
\(\int {\sqrt {{{\ln }^2}x + 1} .\dfrac{{\ln x}}{x}dx = \int {{t^2}dt = \dfrac{{{t^3}}}{3} + C = \dfrac{{{{\left( {\sqrt {{{\ln }^2}x + 1} } \right)}^3}}}{3} + C} } \).
Vì \(F\left( 1 \right) = \dfrac{1}{3}\) nên \(C = 0\)
Vậy \({F^2}\left( e \right) = \dfrac{8}{9}\).
Hướng dẫn giải:
- Tìm \(F\left( x \right)\) thỏa mãn bài toán.
- Thay \(x = {e^2}\) vào \(F\left( x \right)\) và kết luận.
Cho tích phân \(I = \int\limits_0^{\dfrac{\pi }{2}} {\sin x\sqrt {8 + \cos x} dx} \). Đặt \(u = 8 + \cos x\) thì kết quả nào sau đây là đúng?
Đặt \(u = 8 + \cos x \Rightarrow du = - \sin xdx \Rightarrow \sin xdx = - du\)
Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 9\\x = \dfrac{\pi }{2} \Rightarrow t = 8\end{array} \right.\) \( \Rightarrow I = - \int\limits_9^8 {\sqrt u du} = \int\limits_8^9 {\sqrt u du} \)
Hướng dẫn giải:
- Bước 1: Đặt \(t = u\left( x \right)\), đổi cận \(\left\{ \begin{array}{l}x = a \Rightarrow t = u\left( a \right) = a'\\x = b \Rightarrow t = u\left( b \right) = b'\end{array} \right.\) .
- Bước 2: Tính vi phân \(dt = u'\left( x \right)dx\).
- Bước 3: Biến đổi \(f\left( x \right)dx\) thành \(g\left( t \right)dt\).
- Bước 4: Tính tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_{a'}^{b'} {g\left( t \right)dt} \).
Giải thích thêm:
Một số em tính sai vi phân \(u = 8 + \cos x \Rightarrow du = \sin xdx\) và chọn nhầm đáp án C là sai.
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = x{e^x}\) , trục hoành, hai đường thẳng \(x = - 2;x = 3\) có công thức tính là
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = x{e^x}\) , trục hoành, hai đường thẳng \(x = - 2;x = 3\) có công thức tính là \(S = \int\limits_{ - 2}^3 {\left| {x{e^x}} \right|dx} .\)
Hướng dẫn giải:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y =f(x)\) , trục hoành, hai đường thẳng \(x = a;x = b\) có công thức tính là \(S = \int\limits_{ a}^b {\left| {f(x)} \right|dx} .\)
Nếu \(t = u\left( x \right)\) thì:
Nếu \(t = u\left( x \right)\)thì \(dt = u'\left( x \right)dx\).
Hướng dẫn giải:
Sử dụng công thức tính vi phân $dy=y'dx$
Họ nguyên hàm của hàm số \(y=\cos 3x\) là
Ta có \(\int{\cos 3x\,\text{d}x}=\dfrac{\sin 3x}{3}+C.\)
Tìm nguyên hàm $F(x)$ của hàm số \(f(x)=6x+\sin 3x\), biết \(F(0)=\dfrac{2}{3}.\)
$f(x) = 6x + \sin 3x$ $ \Rightarrow \int {f(x)dx} {\rm{\;}} = \int {(6x + \sin 3x)dx} $ $ = \int {6xdx} {\rm{\;}} + \int {\sin 3xdx} = 3{x^2} - \dfrac{1}{3}\cos 3x + C$
$ \Rightarrow F(x) = 3{x^2} - \dfrac{1}{3}\cos 3x + C$
$F(0) = \dfrac{2}{3} \Leftrightarrow {3.0^2} - \dfrac{1}{3}.\cos 0 + C = \dfrac{2}{3} \Leftrightarrow C = 1$
$ \Rightarrow F(x) = 3{x^2} - \dfrac{{\cos 3x}}{3} + 1$
Tìm nguyên hàm của hàm số \(f(x) = \dfrac{x}{{\sqrt {3{x^2} + 2} }}\).
\(\int {\dfrac{x}{{\sqrt {3{{\rm{x}}^2} + 2} }}d{\rm{x}}} = \dfrac{1}{6}\int {\dfrac{{d\left( {3{{\rm{x}}^2} + 2} \right)}}{{\sqrt {3{{\rm{x}}^2} + 2} }}} \) \(= \dfrac{1}{3}\int {\dfrac{{d\left( {3{{\rm{x}}^2} + 2} \right)}}{{2\sqrt {3{{\rm{x}}^2} + 2} }}} = \dfrac{1}{3}\sqrt {3{{\rm{x}}^2} + 2} + C\)
Hướng dẫn giải:
Sử dụng phương pháp đổi biến, chú ý \(xdx = \dfrac{{d\left( {3{x^2} + 2} \right)}}{6}\)
Tính nguyên hàm $I = \int {\dfrac{{\ln \left( {lnx} \right)}}{x}{\rm{d}}x} $ được kết quả nào sau đây?
Đặt $\ln x = t \Rightarrow dt = \dfrac{{dx}}{x}$.
Suy ra $I = \int {\dfrac{{\ln \left( {lnx} \right)}}{x}dx} = \int {\ln t\,dt} $.
Đặt $\left\{ \begin{array}{l}u = \ln t\\dv = dt\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \dfrac{{dt}}{t}\\v = t\end{array} \right.$. Theo công thức tính nguyên hàm từng phần, ta có:
$I = t\ln t - \int {dt} $ $ = t\ln t - t + C = \ln x.\ln \left( {\ln x} \right) - \ln x + C$.
Hướng dẫn giải:
Đặt \(\ln x = t\) rồi dùng phương pháp nguyên hàm từng phần tìm nguyên hàm hàm số thu được.
Tính \(I = \int {x{{\tan }^2}xdx} \) ta được:
\(I = \int {x{{\tan }^2}xdx} = \int {x\left( {\dfrac{1}{{{{\cos }^2}x}} - 1} \right)dx} = \int {x.\dfrac{1}{{{{\cos }^2}x}}dx} - \int {xdx} = {I_1} - {I_2}\)
Ta có: \({I_2} = \int {xdx} = \dfrac{{{x^2}}}{2} + {C_2},{I_1} = \int {x\dfrac{1}{{{{\cos }^2}x}}dx} \)
Đặt $\left\{ \begin{array}{l}u = x\\dv = \dfrac{1}{{{{\cos }^2}x}}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = \tan x\end{array} \right.$
$\begin{array}{l} \Rightarrow {I_1} = x\tan x - \int {\tan xdx} + {C_1} = x\tan x - \int {\dfrac{{\sin x}}{{\cos x}}dx} + {C_1} \\ = x\tan x + \int {\dfrac{{d\left( {\cos x} \right)}}{{\cos x}}} + {C_1} = x\tan x + \ln \left| {\cos x} \right| + {C_1}.\\ \Rightarrow I = x\tan x + \ln \left| {\cos x} \right| + {C_1} - \dfrac{{{x^2}}}{2} - {C_2} = x\tan x + \ln \left| {\cos x} \right| - \dfrac{{{x^2}}}{2} + C.\end{array}$
Hướng dẫn giải:
Sử dụng công thức \({\tan ^2}x = \dfrac{1}{{{{\cos }^2}x}} - 1,\) sau đó tách thành 2 nguyên hàm và sử dụng phương pháp nguyên hàm từng phần.
Tích phân $\int\limits_{ - 1}^5 {\left| {{x^2} - 2x - 3} \right|} dx$ có giá trị bằng:
$\begin{array}{c}\int\limits_{ - 1}^5 {\left| {{x^2} - 2x - 3} \right|dx} = \int\limits_{ - 1}^5 {\left| {(x - 3)(x + 1)} \right|dx} = - \int\limits_{ - 1}^3 {\left( {{x^2} - 2x - 3} \right)dx} + \int\limits_3^5 {\left( {{x^2} - 2x - 3} \right)dx} \\ = - \left. {\left( {\dfrac{{{x^3}}}{3} - {x^2} - 3x} \right)} \right|_{ - 1}^3 + \left. {\left( {\dfrac{{{x^3}}}{3} - {x^2} - 3x} \right)} \right|_3^5 = \dfrac{{64}}{3}.\end{array}$
Hướng dẫn giải:
Phá dấu giá trị tuyệt đối trong từng khoảng rồi tính tích phân.
Biết rằng \(\int\limits_0^1 {x\cos 2xdx} = \dfrac{1}{4}\left( {a\sin 2 + b\cos 2 + c} \right)\) với \(a,b,c \in Z\). Mệnh đề nào sau đây là đúng
$\begin{array}{l}u\left( x \right) = x \Rightarrow u'\left( x \right) = 1\\v'\left( x \right) = \cos 2x \Rightarrow v\left( x \right) = \dfrac{{\sin 2x}}{2}\\ \Rightarrow \int\limits_0^1 {x\cos 2xdx = \left. {\dfrac{x}{2}\sin 2x} \right|_0^1} - \dfrac{1}{2}\int\limits_0^1 {\sin 2xdx} = \left. {\dfrac{x}{2}\sin 2x} \right|_0^1 + \left. {\dfrac{{\cos 2x}}{4}} \right|_0^1\\ = \dfrac{1}{2}\sin 2 + \dfrac{1}{4}\cos 2 - \dfrac{1}{4} = \dfrac{1}{4}\left( {2\sin 2 + \cos 2 - 1} \right)\\ \Rightarrow a = 2;b = 1;c = - 1\end{array}$
Khi đó $a - b + c = 2 - 1 - 1 = 0$
Hướng dẫn giải:
- Bước 1: Đặt \(\left\{ \begin{array}{l}u = f\left( x \right)\\dv = \sin \left( {ax + b} \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = f'\left( x \right)dx\\v = - \dfrac{1}{a}\cos \left( {ax + b} \right)\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}u = f\left( x \right)\\dv = \cos \left( {ax + b} \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = f'\left( x \right)dx\\v = \dfrac{1}{a}\sin \left( {ax + b} \right)\end{array} \right.\)
- Bước 2: Tính tích phân theo công thức \(\int\limits_m^n {f\left( x \right)\sin \left( {ax + b} \right)dx} = \left. {uv} \right|_m^n - \int\limits_m^n {vdu} \) hoặc \(\int\limits_m^n {f\left( x \right)\cos \left( {ax + b} \right)dx} = \left. {uv} \right|_m^n - \int\limits_m^n {vdu} \)
Cho hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục trên đoạn \(\left[ {a;b} \right]\) với \(a < b\). Kí hiệu \({S_1}\) là diện tích hình phẳng giới hạn bởi các đường \(y = 3f(x)\), \(y = 3g(x),\,\,x = a,\,\,x = b,\,\,{S_2}\) là diện tích hình phẳng giới hạn bởi các đường \(y = f(x) - 2,\,\,y = g(x) - 2,\,\,x = a,\,\,x = b\). Khẳng định nào sau đây đúng?
Theo đề bài, ta có:
\({S_1} = \int\limits_a^b {\left| {3f(x) - 3g(x)} \right|dx} = 3\int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \), \({S_2} = \int\limits_a^b {\left| {\left( {f(x) - 2} \right) - \left( {g(x) - 2} \right)} \right|dx} = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)
\( \Rightarrow {S_1} = 3{S_2}\)
Hướng dẫn giải:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số \(y = f(x),y = g(x)\), trục hoành và hai đường thẳng \(x = a;\,\,x = b\) được tính theo công thức : \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \).
Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x},\) trục hoành và đường thẳng \(x=9.\) Khi (H) quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng:
Đk: \(x\ge 0\).
Xét phương trình hoành độ giao điểm \(\sqrt{x}=0\Leftrightarrow x=0\). Khi đó \(V=\pi \int\limits_{0}^{9}{xdx}=\left. \pi \frac{{{x}^{2}}}{2} \right|_{0}^{9}=\frac{81\pi }{2}\)
Hướng dẫn giải:
Sử dụng công thức ứng dụng tích phân để tính thể tích vật tròn xoay.
Thể tích của khối tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành, đường thẳng \(x=a;\,\,x=b\) quanh $Ox$ là \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\).
Cho tích phân $I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x} = \dfrac{{m - \pi }}{{m + \pi }}$, giá trị của $m$ bằng :
Ta có : \(\left( {x\sin x + \cos x} \right)' = \sin x + x\cos x - \sin x = x\cos x\)
$ \Rightarrow I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x} = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{\dfrac{x}{{\cos x}}.x\cos x}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dv} $
Đặt $\left\{ \begin{array}{l}u = \dfrac{x}{{\cos x}}\\{\rm{d}}v = \dfrac{{x\cos x}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}{\rm{d}}x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\rm{d}}u = \dfrac{{x\sin x + \cos x}}{{{{\cos }^2}x}}{\rm{d}}x\\v = - \dfrac{1}{{x\sin x + \cos x}}\end{array} \right..$
Khi đó
$\begin{array}{l}I = \left. { - \dfrac{x}{{\cos x}}.\dfrac{1}{{x\sin x + \cos x}}} \right|_0^{\dfrac{\pi }{4}} + \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{{\rm{d}}x}}{{{{\cos }^2}x}}} = \\ = \dfrac{{ - \dfrac{\pi }{4}}}{{\dfrac{{\sqrt 2 }}{2}}}.\dfrac{1}{{\dfrac{\pi }{4}\dfrac{{\sqrt 2 }}{2} + \dfrac{{\sqrt 2 }}{2}}} + \left. {\tan x} \right|_0^{\dfrac{\pi }{4}}\\ = \dfrac{{ - \dfrac{\pi }{4}}}{{\dfrac{1}{2}\left( {\dfrac{\pi }{4} + 1} \right)}} + 1 = \dfrac{{ - 2\pi }}{{\left( {\pi + 4} \right)}} + 1 = \dfrac{{4 - \pi }}{{4 + \pi }} \Rightarrow m = 4\end{array}$.
Hướng dẫn giải:
- Sử dụng công thức của tích phân từng phần: \(\int\limits_a^b {udv} = \left. {uv} \right|_a^b - \int\limits_a^b {vdu} \).
- Làm xuất hiện dạng vi phân \(f'\left( x \right)dx\)sau đó đặt \(dv = f'\left( x \right)dx\).
- Đồng nhất thức.
Tìm họ nguyên hàm của hàm số $f(x) = {\tan ^5}x$.
$I = \int {f(x)dx} = \int {{{\tan }^5}xdx} $.
Đặt $\tan {\mkern 1mu} x = t \Rightarrow \dfrac{{dx}}{{{{\cos }^2}x}} = dt \Rightarrow ({\tan ^2}x + 1)dx = dt \Rightarrow dx = \dfrac{{dt}}{{{t^2} + 1}}$
Khi đó:
\(\begin{array}{*{20}{l}}{I = \int {{t^5}.\dfrac{{dt}}{{{t^2} + 1}}} = \int {({t^3} - t + \dfrac{t}{{{t^2} + 1}})dt} = \int {{t^3}dt} - \int {tdt} + \int {\dfrac{t}{{{t^2} + 1}}dt} }\\{ = \dfrac{1}{4}{t^4} - \dfrac{1}{2}{t^2} + \dfrac{1}{2}\int {\dfrac{{d({t^2} + 1)}}{{{t^2} + 1}}} = \dfrac{1}{4}{t^4} - \dfrac{1}{2}{t^2} + \dfrac{1}{2}\ln \left| {{t^2} + 1} \right| + C}\\{ = \dfrac{1}{4}{{\tan }^4}x - \dfrac{1}{2}{{\tan }^2}x + \dfrac{1}{2}\ln \left( {{{\tan }^2}x + 1} \right) + C}\\{ = \dfrac{1}{4}{{\tan }^4}x - \dfrac{1}{2}{{\tan }^2}x + \dfrac{1}{2}\ln \left( {\dfrac{1}{{{{\cos }^2}x}}} \right) + C}\\{ = \dfrac{1}{4}{{\tan }^4}x - \dfrac{1}{2}{{\tan }^2}x - \ln \left| {\cos x} \right| + C}\end{array}\)
Hướng dẫn giải:
Đặt \(t = \tan x\) rồi tính \(dx\) theo \(dt\) và thay vào tìm nguyên hàm.
Cho hàm số \(y = \frac{{x - {m^2}}}{{x + 1}}\) (với m là tham số khác 0) có đồ thị là \(\left( C \right)\). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị \(\left( C \right)\) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn \(S = 1\)?
TXĐ: \(D = R\backslash \left\{ { - 1} \right\}\). Ta có \(y' = \frac{{1 + {m^2}}}{{{{\left( {x + 1} \right)}^2}}} > 0\,\,\forall x \ne - 1 \Rightarrow \) Hàm số đồng biến trên \(\left( { - \infty ; - 1} \right);\,\,\left( { - 1; + \infty } \right)\).
\(y = 0 \Rightarrow x = {m^2} \Rightarrow \left( C \right)\) cắt trục hoành tại điểm \(A\left( {{m^2};0} \right)\).
\(x = 0 \Rightarrow y = - {m^2} \Rightarrow \left( C \right)\) cắt trục tung tại điểm \(B\left( {0; - {m^2}} \right)\).
Với $x\in [0;m^2]$ thì $\frac{{x - {m^2}}}{{x + 1}} < \frac{{{m^2} - {m^2}}}{{{m^2} + 1}} = 0$ (do hàm số đồng biến).
Suy ra $\left| {\frac{{x - {m^2}}}{{x + 1}}} \right| = - \frac{{x - {m^2}}}{{x + 1}}$
Khi đó diện tích hình phẳng giới hạn bởi đồ thị hàm số \(\left( C \right)\) và hai trục tọa độ là:
\(\begin{array}{l}S = \int\limits_0^{{m^2}} {\left| {\frac{{x - {m^2}}}{{x + 1}}} \right|dx} \\ = - \int\limits_0^{{m^2}} {\frac{{x - {m^2}}}{{x + 1}}dx} \\ = - \int\limits_0^{{m^2}} {\frac{{x + 1 - 1 - {m^2}}}{{x + 1}}dx} \\= - \int\limits_0^{{m^2}} {\left( {1 - \frac{{1 + {m^2}}}{{x + 1}}} \right)dx}\\= - \left[ {\int\limits_0^{{m^2}} {dx} - \int\limits_0^{{m^2}} {\frac{{1 + {m^2}}}{{x + 1}}} dx} \right] \\= - \left[ {\left. x \right|_0^{{m^2}} - \left( {1 + {m^2}} \right)\left. {\ln \left| {x + 1} \right|} \right|_0^{{m^2}}} \right] \\= - \left[ {{m^2} - \left( {1 + {m^2}} \right)\ln \left( {{m^2} + 1} \right)} \right]\\= \left( {1 + {m^2}} \right)\ln \left( {{m^2} + 1} \right) - {m^2} = 1\\ \Leftrightarrow \left( {{m^2} + 1} \right)\ln \left( {{m^2} + 1} \right) - {m^2} - 1 = 0\\ \Leftrightarrow \left( {{m^2} + 1} \right)\left[ {\ln \left( {{m^2} + 1} \right) - 1} \right] = 0\\ \Leftrightarrow \ln \left( {{m^2} + 1} \right) = 1 \Leftrightarrow {m^2} + 1 = e \Leftrightarrow m = \pm \sqrt {e - 1} \end{array}\)
Hướng dẫn giải:
Sử dụng công thức ứng dụng tích phân để tính diện tích hình phẳng.
Đề thi liên quan
-
Đề kiểm tra 15 phút chương 3: Nguyên hàm - Đề số 1
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 3: Nguyên hàm - Đề số 2
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 3: Nguyên hàm - Đề số 3
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 3: Nguyên hàm - Đề số 1
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 3: Nguyên hàm - Đề số 2
-
25 câu hỏi
-
45 phút
-

