Mặt cầu $\left( S \right)$ có tâm \(I( - 1;2; - 5)\) cắt mặt phẳng \(\left( P \right):2x - 2y - z + 10 = 0\) theo thiết diện là hình tròn có diện tích \(3\pi \). Phương trình của $\left( S \right)$ là:
A.
\({x^2} + {y^2} + {z^2} + 2x - 4y + 10z + 18 = 0\)
B.
\({(x + 1)^2} + {(y - 2)^2} + {(z + 5)^2} = 25\)
C.
\({(x + 1)^2} + {(y - 2)^2} + {(x - 5)^2} = 16\)
D.
\({x^2} + {y^2} + {z^2} + 2x - 4y + 10z + 12 = 0\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
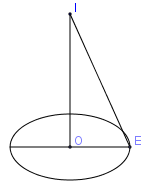
Gọi $O$ là tâm của đường tròn thiết diện, $E$ là một điểm thuộc đường tròn.
Ta có: $IO = d\left( {I,(P)} \right);R = IE$
\(IO = d\left( {I,(P)} \right) = \dfrac{{|2.( - 1) - 2.2 + 5 + 10|}}{{\sqrt {{2^2} + {2^2} + 1} }} = 3\)
\(S = 3\pi = \pi .O{E^2} \Leftrightarrow O{E^2} = 3\)
Tam giác $IOE$ vuông tại $O$ nên \({R^2} = I{E^2} = I{O^2} + O{E^2} = 3 + 9 = 12.\)
Suy ra phương trình mặt cầu $\left( S \right)$ là:
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 5} \right)^2} = 12\) hay \({x^2} + {y^2} + {z^2} + 2x - 4y + 10z + 18 = 0\)
Hướng dẫn giải:
+ Xác định bán kính mặt cầu $\left( S \right)$
+ Phương trình mặt cầu: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
Gọi $O$ là tâm của đường tròn thiết diện, $E$ là một điểm thuộc đường tròn.
Ta có: $IO = d\left( {I,(P)} \right);R = IE$
\(IO = d\left( {I,(P)} \right) = \dfrac{{|2.( - 1) - 2.2 + 5 + 10|}}{{\sqrt {{2^2} + {2^2} + 1} }} = 3\)
\(S = 3\pi = \pi .O{E^2} \Leftrightarrow O{E^2} = 3\)
Tam giác $IOE$ vuông tại $O$ nên \({R^2} = I{E^2} = I{O^2} + O{E^2} = 3 + 9 = 12.\)
Suy ra phương trình mặt cầu $\left( S \right)$ là:
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 5} \right)^2} = 12\) hay \({x^2} + {y^2} + {z^2} + 2x - 4y + 10z + 18 = 0\)

Hướng dẫn giải:
+ Xác định bán kính mặt cầu $\left( S \right)$
+ Phương trình mặt cầu: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
CÂU HỎI CÙNG CHỦ ĐỀ
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = t{\rm{ }}}\\{y = 8 + 4t}\\{z = 3 + 2t}\end{array}} \right.\) và mặt phẳng $\left( P \right):x + y + z - 7 = 0.$ Phương trình đường thẳng \(\Delta '\) là hình chiếu vuông góc của \(\Delta \) trên \(\left( P \right)\) là:
Trong không gian với hệ trục tọa độ $Oxyz$, cho các phương trình sau, phương trình nào không phải là phương trình của mặt cầu?
Cho số phức $z$ thỏa mãn $\left| {z - 2} \right| = 2$. Biết rằng tập hợp các điểm biểu diễn các số phức $w = \left( {1 - i} \right)z + i$ là một đường tròn. Tính bán kính $r$ của đường tròn đó
Trong không gian với hệ trục tọa độ Oxyz, cho 2 điểm \(A(2;1;0),\,\,B(1;-1;3)\). Mặt phẳng qua AB và vuông góc với mặt phẳng (P): \(x+3y-2z-1=0\) có phương trình là
Trong không gian với hệ tọa độ $Oxyz$, mặt cầu $\left( S \right)$ có tâm $I\left( {1,2, - 3} \right)$ và đi qua điểm $A\left( {1,0,4} \right)$ có phương trình là
Cho hai điểm \(A\left( {1; - 2;0} \right),B\left( {0;1;1} \right)\), độ dài đường cao \(OH\) của tam giác \(OAB\) là:
Viết phương trình mặt phẳng $\left( P \right)$ song song với mặt phẳng $\left( Q \right):x + y - z - 2 = 0$ và cách $\left( Q \right)$ một khoảng là \(2\sqrt 3 \) .
Trong không gian với hệ tọa độ $Oxyz$, phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm $M\left( {2;3;3} \right),{\rm{ }}N\left( {2; - 1; - 1} \right),{\rm{ }}P\left( { - 2; - 1;3} \right)$ và có tâm thuộc mặt phẳng \((\alpha ):2x + 3y - z + 2 = 0\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hai đường thẳng
\({d_1}:\left\{ \begin{array}{l}x = t\\y = - 1 - 4t\\z = 6 + 6t\end{array} \right.\) và \(\,{d_2}:\dfrac{x}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{{ - 5}}\).
Trong các phương trình sau đây, phương trình nào là phương trình của đường thẳng \({d_3}\) qua \(M\left( {1; - 1;2} \right)\) và vuông góc với cả \({d_1},\,\,{d_2}.\)
Kí hiệu \(a,b\) lần lượt là phần thực và phần ảo của số phức \(3 - 2\sqrt 2 i\). Tìm \(a,b.\)
Gọi \({z_1};{z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 5 = 0\). Tính \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\).
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\dfrac{{x - 3}}{1} = \dfrac{{y - 3}}{3} = \dfrac{z}{2}\), mặt phẳng \(\left( \alpha \right):x + y - z + 3 = 0\) và điểm \(A\left( {1;2 - 1} \right)\). Đường thẳng \(\Delta \) đi qua \(A\) cắt \(d\) và song song với mặt phẳng \(\left( \alpha \right)\) có phương trình là:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( -1;2;-4 \right)\) và \(B\left( 1;0;2 \right)\). Viết phương trình đường thẳng d đi qua hai điểm A và B.
Biết số phức $z = x + yi{\rm{ }}\left( {x;y \in \mathbb{R}} \right)$ thỏa mãn đồng thời các điều kiện $\left| {z - \left( {3 + 4i} \right)} \right| = \sqrt 5 $ và biểu thức $P = {\left| {z + 2} \right|^2} - {\left| {z - i} \right|^2}$ đạt giá trị lớn nhất. Tính $\left| z \right|$.
Tìm nguyên hàm của hàm số \(f\left( x \right)=3\cos x+\dfrac{1}{{{x}^{2}}}\) trên \(\left( 0;\,+\infty \right)\).

