Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
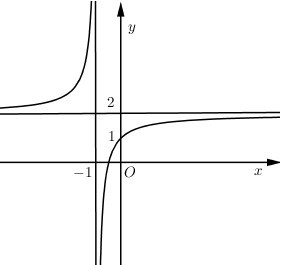
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có \(\left\{ \begin{align}& \xrightarrow{TCN}y=\dfrac{2}{c}=2\Rightarrow c=1 \\ & \xrightarrow{TCD}x=-\dfrac{d}{c}=-\dfrac{d}{1}=-1\Rightarrow d=1 \\ \end{align} \right.\)
Hàm số có dạng \(y = \dfrac{{2x + b}}{{x + 1}}\left( C \right)\).
Ta có điểm \(\left( {0;1} \right) \in \left( C \right)\).
Thay \(x = 0\) và \(y = 1\) vào hàm số ta được \(1 = \dfrac{{2.0 + b}}{{0 + 1}} \Rightarrow b = 1\) \( \Rightarrow b + c + d = 3\).
Hướng dẫn giải:
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số \( \Rightarrow c,d\).
- Tìm điểm đi qua của đồ thị hàm số \( \Rightarrow b\).
- Thay các giá trị tìm được vào kiểm tra các đáp án.
Giải thích thêm:
HS thường nhầm lẫn trong việc xác định tiệm cận đứng \(x = \dfrac{d}{c}\) dẫn đến tính ra \(d = - 1\) và chọn nhầm đáp án A là sai.
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có \(\left\{ \begin{align}& \xrightarrow{TCN}y=\dfrac{2}{c}=2\Rightarrow c=1 \\ & \xrightarrow{TCD}x=-\dfrac{d}{c}=-\dfrac{d}{1}=-1\Rightarrow d=1 \\ \end{align} \right.\)
Hàm số có dạng \(y = \dfrac{{2x + b}}{{x + 1}}\left( C \right)\).
Ta có điểm \(\left( {0;1} \right) \in \left( C \right)\).
Thay \(x = 0\) và \(y = 1\) vào hàm số ta được \(1 = \dfrac{{2.0 + b}}{{0 + 1}} \Rightarrow b = 1\) \( \Rightarrow b + c + d = 3\).
Hướng dẫn giải:
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số \( \Rightarrow c,d\).
- Tìm điểm đi qua của đồ thị hàm số \( \Rightarrow b\).
- Thay các giá trị tìm được vào kiểm tra các đáp án.
Giải thích thêm:
HS thường nhầm lẫn trong việc xác định tiệm cận đứng \(x = \dfrac{d}{c}\) dẫn đến tính ra \(d = - 1\) và chọn nhầm đáp án A là sai.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên:
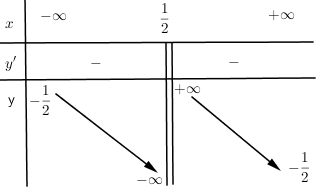
Khẳng định nào sau đây là đúng?
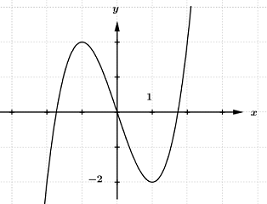
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt.
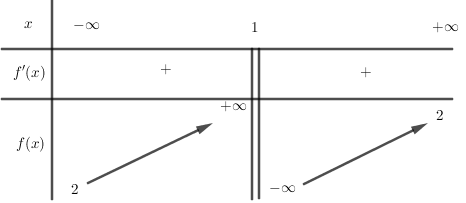
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai?
Cho hàm số \(y = \dfrac{5}{3}{x^3} - {x^2} + 4\) có đồ thị \((C)\). Tiếp tuyến của \((C)\) tại điểm có hoành độ \({x_0} = 3\) có hệ số góc là:
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{5x + 1}}{{3x - 2}}\) là
Hàm số \(y = \dfrac{{\sqrt {{x^2} - 2x + 1} }}{{x - 1}}\) xác định khi
Đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}+2x-1\) cắt đồ thị hàm số \(y={{x}^{2}}-3x+1\) tại hai điểm phân biệt \(A,\,\,B.\) Tính độ dài \(AB.\)
Đề thi THPT QG - 2021 - mã 103
Đồ thị của hàm số \(y = - {x^3} + 2{x^2} - 1\) cắt trục tung tại điểm có tung độ bằng:
Cho hàm số $y = \dfrac{{3x + 1}}{{x + 2}}\left( C \right).$ Các đường tiệm cận của (C) cùng với 2 trục tọa độ tạo thành hình chữ nhật có diện tích bằng:
Cho hàm số \(y = \dfrac{{2x - 2}}{{x - 2}}\) có đồ thị là\(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\)thỏa mãn bài toán. Tìm giá trị của \(S\).