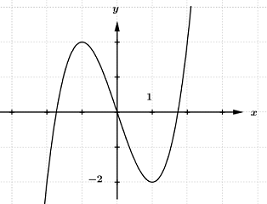
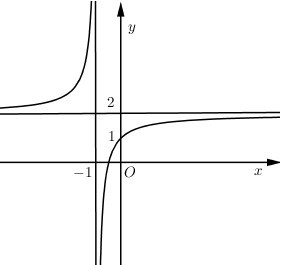
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt.
A.
\(m > 2.\)
B.
\(m < - 1.\)
C.
\( - 1 < m <- \dfrac{1}{3}.\)
D.
\(1 < m < 2.\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
Dựa vào đồ thị hàm số \(y = f\left( x \right)\) ta suy ra được đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) như sau:
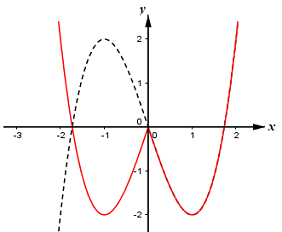
Số nghiệm của phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = 3m + 1\) song song với trục hoành.
Do đó để phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có 4 nghiệm phân biệt thì \( - 2 < 3m + 1 < 0 \Leftrightarrow - 1 < m < - \dfrac{1}{3}\).
Hướng dẫn giải:
- Vẽ đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\).
+ Vẽ đồ thị hàm số \(y = f\left( x \right)\).
+ Xóa đi phần đồ thị hàm số nằm ở bên trái trục tung.
+ Lấy đối xứng phần đồ thị hàm số nằm ở bên phải trục tung qua trục tung.
- Biện luận nghiệm để tìm tham số m: Số nghiệm của phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = 3m + 1\) song song với trục hoành.
Dựa vào đồ thị hàm số \(y = f\left( x \right)\) ta suy ra được đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) như sau:

Số nghiệm của phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = 3m + 1\) song song với trục hoành.
Do đó để phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có 4 nghiệm phân biệt thì \( - 2 < 3m + 1 < 0 \Leftrightarrow - 1 < m < - \dfrac{1}{3}\).
Hướng dẫn giải:
- Vẽ đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\).
+ Vẽ đồ thị hàm số \(y = f\left( x \right)\).
+ Xóa đi phần đồ thị hàm số nằm ở bên trái trục tung.
+ Lấy đối xứng phần đồ thị hàm số nằm ở bên phải trục tung qua trục tung.
- Biện luận nghiệm để tìm tham số m: Số nghiệm của phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = 3m + 1\) song song với trục hoành.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên:
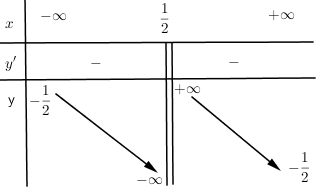
Khẳng định nào sau đây là đúng?
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai?
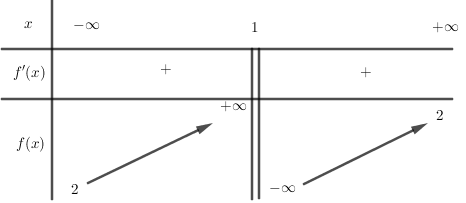
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:
Chọn kết luận đúng:
Cho hàm số \(y = \dfrac{5}{3}{x^3} - {x^2} + 4\) có đồ thị \((C)\). Tiếp tuyến của \((C)\) tại điểm có hoành độ \({x_0} = 3\) có hệ số góc là:
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{5x + 1}}{{3x - 2}}\) là
Hàm số \(y = \dfrac{{\sqrt {{x^2} - 2x + 1} }}{{x - 1}}\) xác định khi
Đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}+2x-1\) cắt đồ thị hàm số \(y={{x}^{2}}-3x+1\) tại hai điểm phân biệt \(A,\,\,B.\) Tính độ dài \(AB.\)
Cho hàm số $y = \dfrac{{3x + 1}}{{x + 2}}\left( C \right).$ Các đường tiệm cận của (C) cùng với 2 trục tọa độ tạo thành hình chữ nhật có diện tích bằng:
Đề thi THPT QG - 2021 - mã 103
Đồ thị của hàm số \(y = - {x^3} + 2{x^2} - 1\) cắt trục tung tại điểm có tung độ bằng:
Cho hàm số \(y = \dfrac{{2x - 2}}{{x - 2}}\) có đồ thị là\(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\)thỏa mãn bài toán. Tìm giá trị của \(S\).

