Cho hàm số $y = f\left( x \right)$ có bảng biến thiên:
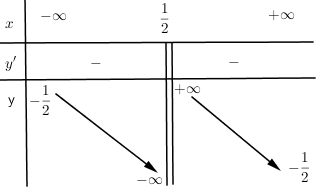
Khẳng định nào sau đây là đúng?
A.
Đồ thị hàm số có tiệm cận đứng là $x = \dfrac{{ - 1}}{2}$
B.
Đồ thị hàm số có tiệm cận đứng là $x = \dfrac{1}{2}$
C.
Hàm số luôn đồng biến trên $R$
D.
Đồ thị hàm số có tiệm cận ngang là $y = \dfrac{1}{2}$
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
$x = \dfrac{1}{2}$ là tiệm cận đứng của đồ thị hàm số
$y = - \dfrac{1}{2}$ là tiệm cận ngang của đồ thị hàm số
Hàm số nghịch biến trên $\left( { - \infty ;\,\dfrac{1}{2}} \right)$ và $\left( {\dfrac{1}{2};\, + \infty } \right)$
Hướng dẫn giải:
Quan sát bảng biến thiên, tìm các tiệm cận đứng, tiệm cận ngang của đồ thị hàm số và tìm các khoảng đồng biến, nghịch biến của hàm số.
Giải thích thêm:
HS thường nhầm lẫn khi tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số.
$x = \dfrac{1}{2}$ là tiệm cận đứng của đồ thị hàm số
$y = - \dfrac{1}{2}$ là tiệm cận ngang của đồ thị hàm số
Hàm số nghịch biến trên $\left( { - \infty ;\,\dfrac{1}{2}} \right)$ và $\left( {\dfrac{1}{2};\, + \infty } \right)$
Hướng dẫn giải:
Quan sát bảng biến thiên, tìm các tiệm cận đứng, tiệm cận ngang của đồ thị hàm số và tìm các khoảng đồng biến, nghịch biến của hàm số.
Giải thích thêm:
HS thường nhầm lẫn khi tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số.
CÂU HỎI CÙNG CHỦ ĐỀ
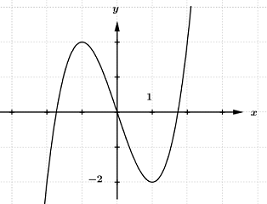
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt.
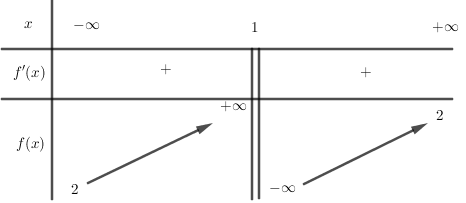
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai?
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:
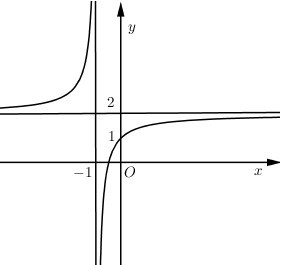
Chọn kết luận đúng:
Cho hàm số \(y = \dfrac{5}{3}{x^3} - {x^2} + 4\) có đồ thị \((C)\). Tiếp tuyến của \((C)\) tại điểm có hoành độ \({x_0} = 3\) có hệ số góc là:
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{5x + 1}}{{3x - 2}}\) là
Hàm số \(y = \dfrac{{\sqrt {{x^2} - 2x + 1} }}{{x - 1}}\) xác định khi
Đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}+2x-1\) cắt đồ thị hàm số \(y={{x}^{2}}-3x+1\) tại hai điểm phân biệt \(A,\,\,B.\) Tính độ dài \(AB.\)
Đề thi THPT QG - 2021 - mã 103
Đồ thị của hàm số \(y = - {x^3} + 2{x^2} - 1\) cắt trục tung tại điểm có tung độ bằng:
Cho hàm số $y = \dfrac{{3x + 1}}{{x + 2}}\left( C \right).$ Các đường tiệm cận của (C) cùng với 2 trục tọa độ tạo thành hình chữ nhật có diện tích bằng:
Cho hàm số \(y = \dfrac{{2x - 2}}{{x - 2}}\) có đồ thị là\(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\)thỏa mãn bài toán. Tìm giá trị của \(S\).

