Cho khối chóp S.ABCD có thể tích bằng \(4{a^3}\), đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Biết diện tích tam giác SAB bằng \({a^2}\). Tính khoảng cách từ M tới mặt phẳng \(\left( {SAB} \right)\).
A.
\(12a\)
B.
\(6a\)
C.
\(3a\)
D.
\(4a\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
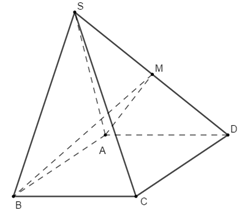
Vì M là trung điểm của SD nên \(\frac{{{V_{SABM}}}}{{{V_{SABD}}}} = \frac{{SM}}{{SD}} = \frac{1}{2}\)
Mà \(\frac{{{V_{SABD}}}}{{{V_{SABCD}}}} = \frac{1}{2} \Rightarrow {V_{SABD}} = \frac{1}{2}.4{a^3} = 2{a^3}\)
\( \Rightarrow {V_{SABM}} = {a^3} = \frac{1}{3}.d\left( {M;\left( {SAB} \right)} \right).{S_{SAB}} \Leftrightarrow d\left( {M;\left( {SAB} \right)} \right) = \frac{{3{a^3}}}{{{a^2}}} = 3a\)
Hướng dẫn giải:
Sử dụng tỉ số thể tích để tính \({V_{SABM}}\).
Áp dụng công thức tính thể tích để suy ra \({d_{M;\left( {SAB} \right)}}\)

Vì M là trung điểm của SD nên \(\frac{{{V_{SABM}}}}{{{V_{SABD}}}} = \frac{{SM}}{{SD}} = \frac{1}{2}\)
Mà \(\frac{{{V_{SABD}}}}{{{V_{SABCD}}}} = \frac{1}{2} \Rightarrow {V_{SABD}} = \frac{1}{2}.4{a^3} = 2{a^3}\)
\( \Rightarrow {V_{SABM}} = {a^3} = \frac{1}{3}.d\left( {M;\left( {SAB} \right)} \right).{S_{SAB}} \Leftrightarrow d\left( {M;\left( {SAB} \right)} \right) = \frac{{3{a^3}}}{{{a^2}}} = 3a\)
Hướng dẫn giải:
Sử dụng tỉ số thể tích để tính \({V_{SABM}}\).
Áp dụng công thức tính thể tích để suy ra \({d_{M;\left( {SAB} \right)}}\)
CÂU HỎI CÙNG CHỦ ĐỀ
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:

Tìm TXĐ của hàm số \(y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}\)
Cho hàm số \(y = \dfrac{{2x - 2}}{{x - 2}}\) có đồ thị là\(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\)thỏa mãn bài toán. Tìm giá trị của \(S\).
Tìm giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$
Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).
Tập hợp nghiệm của phương trình \({\log _3}\left( {{9^{50}} + 6{x^2}} \right) = {\log _{\sqrt 3 }}\left( {{3^{50}} + 2x} \right)\) là:
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
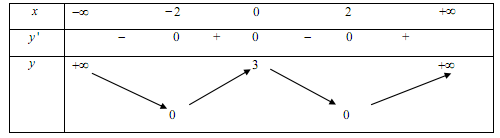
Khẳng định nào sau đây là khẳng định đúng?
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
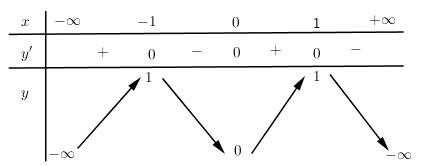
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Cho hàm số $y = {x^4} - 4{x^2} + 3$. Tìm tất cả các giá trị của tham số $m$ sao cho phương trình $\left| {{x^4} - 4{x^2} + 3} \right| = m$ có $4$ nghiệm phân biệt.
Đơn giản biểu thức $P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right)\,\,\,\,(a,b > 0)$ ta được:
Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:
Cho hàm số \(y = {3^x} + \ln 3\). Chọn mệnh đề đúng:
Cho $x, y$ là các số thực thỏa mãn \({\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của biểu thức \(P = 2x - y\).

