Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
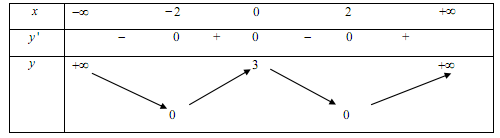
Đáp án A: Hàm số đạt cực đại tại $x = 0$ và $y = 3$ là giá trị cực đại của hàm số nên A sai.
Đáp án B: GTNN và giá trị cực tiểu của hàm số là $y = 0$ nên B đúng và C sai.
Đáp án D: Hàm số không có GTLN vì $\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty $.
Hướng dẫn giải:
Xét tính đúng, sai của từng đáp án. Sử dụng các định nghĩa GTLN, GTNN, giá trị cực đại, giá trị cực tiểu của hàm số.
Giải thích thêm:
HS thường nhầm lần giữa GTLN với GTCĐ, GTNN với GTCT nên cần phân biệt rõ ràng mối quan hệ giữa các giá trị này.
Đáp án A: Hàm số đạt cực đại tại $x = 0$ và $y = 3$ là giá trị cực đại của hàm số nên A sai.
Đáp án B: GTNN và giá trị cực tiểu của hàm số là $y = 0$ nên B đúng và C sai.
Đáp án D: Hàm số không có GTLN vì $\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty $.
Hướng dẫn giải:
Xét tính đúng, sai của từng đáp án. Sử dụng các định nghĩa GTLN, GTNN, giá trị cực đại, giá trị cực tiểu của hàm số.
Giải thích thêm:
HS thường nhầm lần giữa GTLN với GTCĐ, GTNN với GTCT nên cần phân biệt rõ ràng mối quan hệ giữa các giá trị này.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
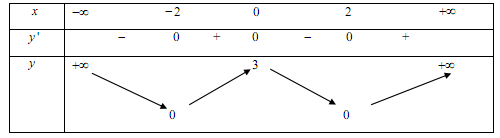
Khẳng định nào sau đây là khẳng định đúng:
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x$ trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ lần lượt là
Tìm tất cả các giá trị của tham số $m$ để đường thẳng $y = - 2x + m$ cắt đồ thị $(H)$ của hàm số $y = \dfrac{{2x + 3}}{{x + 2}}$ tại hai điểm$A,{\text{ }}B$ phân biệt sao cho $P = k_1^{2018} + k_2^{2018}$ đạt giá trị nhỏ nhất (với ${k_1},{k_2}$ là hệ số góc của tiếp tuyến tại $A,{\text{ }}B$ của đồ thị $(H)$.
Cho hàm số $y = f\left( x \right)$ xác định trên $R\backslash \left\{ { - 1;\,1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
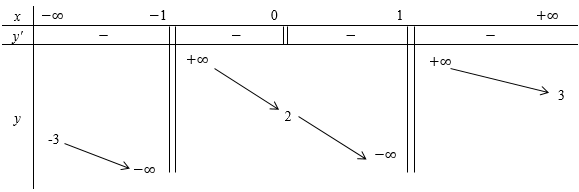
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt.
Cho hàm số $y = {x^4} - 2m{x^2} + 3m + 2.$ Tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành tam giác đều là:
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
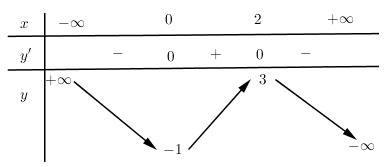
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên trên khoảng $\left( {0;2} \right)$ như sau:
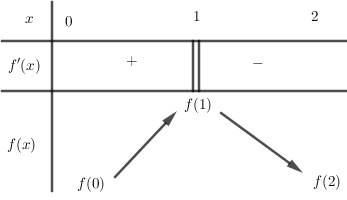
Khẳng định nào sau đây là khẳng định đúng:
Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$
Hàm số $y = - {x^4} - 2{x^2} + 3$ nghịch biến trên:
Cho hàm số $y = f(x)$ liên tục và có đạo hàm cấp hai trên $R$. Đồ thị của các hàm số $y = f(x),y = f'(x),y = f''(x)$ lần lượt là các đường cong nào trong hình vẽ bên.
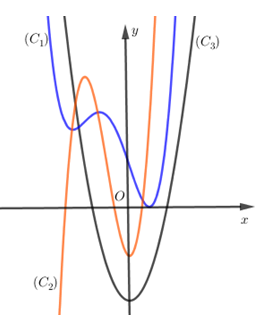
Cho $(C)$ là đồ thị hàm số $y = \dfrac{{x + 1}}{{x - 2}}$. Tìm các điểm trên $(C)$ sao cho tổng khoảng cách từ điểm đó đến 2 tiệm cận là nhỏ nhất:
Tìm giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$
Cho các dạng đồ thị (I), (II), (III) như hình dưới đây:
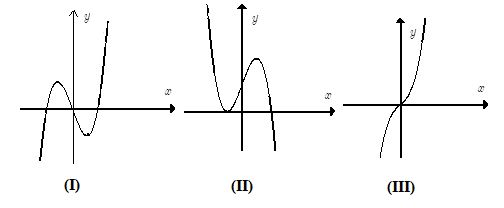
Liệt kê tất cả các dạng có thể biểu diễn đồ thị hàm số \(y = {x^3} + b{x^2} - x + d\).
Cho các số thực $x, y$ thỏa mãn ${\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + 2xy \leqslant 32.$ Giá trị nhỏ nhất $m$ của biểu thức $A = {x^3} + {y^3} + 3\left( {xy - 1} \right)\left( {x + y - 2} \right)$ là: