Cho $(C)$ là đồ thị hàm số $y = \dfrac{{x + 1}}{{x - 2}}$. Tìm các điểm trên $(C)$ sao cho tổng khoảng cách từ điểm đó đến 2 tiệm cận là nhỏ nhất:
A.
$\left( 1;1 \right)$
B.
$\left( {2 + \sqrt 3 ;1 + \sqrt 3 } \right)$ và $\left( {2 - \sqrt 3 ;1 - \sqrt 3 } \right)$
C.
$\left( {1 - \sqrt 3 ;1 - \sqrt 3 } \right)$
D.
$\left( {1 + \sqrt 3 ;1 + \sqrt 3 } \right)$
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
Gọi $M\left( {m;\dfrac{{m + 1}}{{m - 2}}} \right) \in \left( C \right)\,\left( {m \ne 2} \right)$. Tổng khoảng cách từ M đến 2 đường tiệm cận $x = 2 $ và $y = 1$ là
$S = \left| {m - 2} \right| + \left| {\dfrac{{m + 1}}{{m - 2}} - 1} \right| = \left| {m - 2} \right| + \dfrac{3}{{\left| {m - 2} \right|}} \geqslant 2\sqrt {\left| {m - 2} \right|.\dfrac{3}{{\left| {m - 2} \right|}}} = 2\sqrt 3 $
Dấu “=” xảy ra $ \Leftrightarrow \left| {m - 2} \right| = \dfrac{3}{{\left| {m - 2} \right|}} \Leftrightarrow \left| {m - 2} \right| = \sqrt 3 \Leftrightarrow m = 2 \pm \sqrt 3 $
Vậy có 2 điểm thỏa mãn bài toán là ${M_1}\left( {2 + \sqrt 3 ;1 + \sqrt 3 } \right),{M_2}\left( {2 - \sqrt 3 ;1 - \sqrt 3 } \right)$
Hướng dẫn giải:
- Gọi điểm $M$ có tọa độ thỏa mãn phương trình hàm số.
- Tìm phương trình hai đường tiệm cận của đồ thị hàm số.
- Sử dụng công thức tính khoảng cách để tính tổng khoảng cách của điểm $M$ đến hai tiệm cận.
- Tìm GTNN của biểu thức ở trên, từ đó suy ra $m$.
Gọi $M\left( {m;\dfrac{{m + 1}}{{m - 2}}} \right) \in \left( C \right)\,\left( {m \ne 2} \right)$. Tổng khoảng cách từ M đến 2 đường tiệm cận $x = 2 $ và $y = 1$ là
$S = \left| {m - 2} \right| + \left| {\dfrac{{m + 1}}{{m - 2}} - 1} \right| = \left| {m - 2} \right| + \dfrac{3}{{\left| {m - 2} \right|}} \geqslant 2\sqrt {\left| {m - 2} \right|.\dfrac{3}{{\left| {m - 2} \right|}}} = 2\sqrt 3 $
Dấu “=” xảy ra $ \Leftrightarrow \left| {m - 2} \right| = \dfrac{3}{{\left| {m - 2} \right|}} \Leftrightarrow \left| {m - 2} \right| = \sqrt 3 \Leftrightarrow m = 2 \pm \sqrt 3 $
Vậy có 2 điểm thỏa mãn bài toán là ${M_1}\left( {2 + \sqrt 3 ;1 + \sqrt 3 } \right),{M_2}\left( {2 - \sqrt 3 ;1 - \sqrt 3 } \right)$
Hướng dẫn giải:
- Gọi điểm $M$ có tọa độ thỏa mãn phương trình hàm số.
- Tìm phương trình hai đường tiệm cận của đồ thị hàm số.
- Sử dụng công thức tính khoảng cách để tính tổng khoảng cách của điểm $M$ đến hai tiệm cận.
- Tìm GTNN của biểu thức ở trên, từ đó suy ra $m$.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
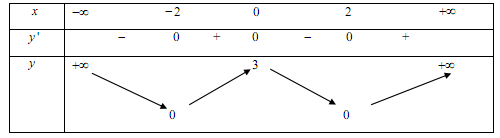
Khẳng định nào sau đây là khẳng định đúng:
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x$ trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ lần lượt là
Tìm tất cả các giá trị của tham số $m$ để đường thẳng $y = - 2x + m$ cắt đồ thị $(H)$ của hàm số $y = \dfrac{{2x + 3}}{{x + 2}}$ tại hai điểm$A,{\text{ }}B$ phân biệt sao cho $P = k_1^{2018} + k_2^{2018}$ đạt giá trị nhỏ nhất (với ${k_1},{k_2}$ là hệ số góc của tiếp tuyến tại $A,{\text{ }}B$ của đồ thị $(H)$.
Cho hàm số $y = f\left( x \right)$ xác định trên $R\backslash \left\{ { - 1;\,1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
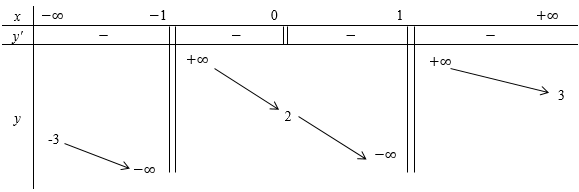
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt.
Cho hàm số $y = {x^4} - 2m{x^2} + 3m + 2.$ Tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành tam giác đều là:
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên trên khoảng $\left( {0;2} \right)$ như sau:
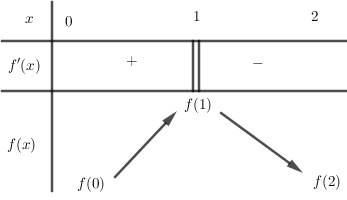
Khẳng định nào sau đây là khẳng định đúng:
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
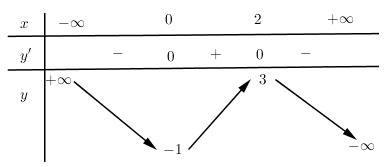
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Hàm số $y = - {x^4} - 2{x^2} + 3$ nghịch biến trên:
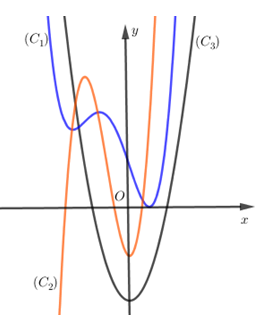
Cho hàm số $y = f(x)$ liên tục và có đạo hàm cấp hai trên $R$. Đồ thị của các hàm số $y = f(x),y = f'(x),y = f''(x)$ lần lượt là các đường cong nào trong hình vẽ bên.
Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$
Tìm giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$
Cho các dạng đồ thị (I), (II), (III) như hình dưới đây:
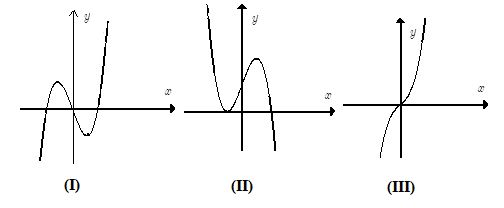
Liệt kê tất cả các dạng có thể biểu diễn đồ thị hàm số \(y = {x^3} + b{x^2} - x + d\).
Cho các số thực $x, y$ thỏa mãn ${\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + 2xy \leqslant 32.$ Giá trị nhỏ nhất $m$ của biểu thức $A = {x^3} + {y^3} + 3\left( {xy - 1} \right)\left( {x + y - 2} \right)$ là:
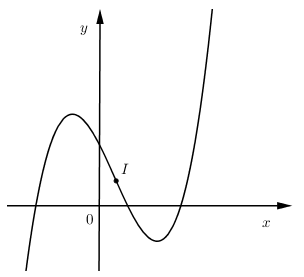
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng: