Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Quế Sơn
Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Quế Sơn
-
Hocon247
-
30 câu hỏi
-
60 phút
-
106 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho hàm số \(y = \dfrac{3 }{{x - 2}}\). Số tiệm cận của đồ thị hàm số bằng bao nhiêu?
\(y = \dfrac{3}{{x - 2}}\)
TXĐ: \(D = R\backslash {\rm{\{ }}2\}\)
\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} \dfrac{3}{{x - 2}} = + \infty \\\mathop {\lim }\limits_{X \to {2^ - }} \dfrac{3}{{x - 2}} = - \infty \end{array} \right\} \Rightarrow TCĐ:x = 2\)
\(\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{3}{{x - 2}} = 0 \Rightarrow TCN y=0\)
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{1 - 2x} }{ { - x + 2}}\)
\(y = \dfrac{{1 - 2x}}{{ - x + 2}}\)
TXĐ: \(D = R\backslash {\rm{\{ }}2\}\)
\(\begin{array}{l}\mathop {\lim }\limits_{X \to \pm \infty } \dfrac{{1 - 2x}}{{ - x + 2}} = 2 \Rightarrow TCN:y = 2\\\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ - }} \dfrac{{1 - 2x}}{{ - x + 2}} = - \infty \\\mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{1 - 2x}}{{ - x + 2}} = + \infty \end{array} \right\} \\\Rightarrow TCĐ:x = 2\end{array}\)
Hàm số \(y = {x^3} - 3{x^2} + 3x - 4\) có bao nhiêu cực trị?
\(y = {x^3} - 3{x^2} + 3x - 4\)
TXD:D = R
\(\begin{array}{l}y' = 3{x^2} - 6x + 3\\y' = 0 \Leftrightarrow 3{x^2} - 6x + 3 = 0\\ \Leftrightarrow x = 1\end{array}\)
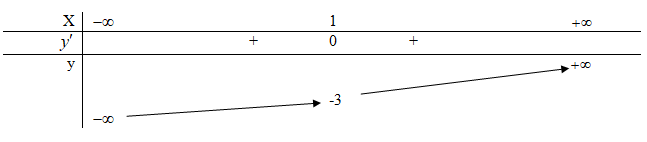
Hàm số đồng biến trên R nên không có cực trị.
Giá trị cực đại của hàm số \(y = {x^3} - 12x - 1\).
\(y = {x^3} - 12x - 1\)
TXD:D = R
\(\begin{array}{l}y' = 3{x^2} - 12\\y' = 0 \Leftrightarrow 3{x^2} - 12 = 0\\ \Leftrightarrow {x^2} - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\end{array}\)
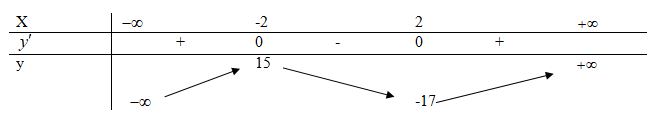
\(\begin{array}{l}{x_{cd}} = - 2 \Rightarrow {y_{cd}} = 15\\{x_{ct}} = 2 \Rightarrow {y_{ct}} = - 17\end{array}\)
Đồ thi hàm số nào dưới đây có tiệm cận đứng
Đồ thị hàm đa thức không có đường tiệm cận nên loại A, B.
Đáp án C có đường tiệm cận đứng là x=1 nên thỏa mãn.
Cho hàm số \(y = \dfrac{{x + 1} }{ {x - 1}}\). Khẳng định nào sau đây là đúng?
\(y = \dfrac{{x + 1}}{{x - 1}}\)
TXĐ: \(D = R\backslash {\rm{\{ }}1\}\)
\(y' = \dfrac{{ - 2}}{{{{\left( {x - 1} \right)}^2}}} < 0\forall x \ne 1\)
Hàm nghịch biến trên \(( - \infty ,1)\) và \((1, + \infty )\)
Cho hàm số y = f(x) xác định trên khoảng \((0; + \infty )\) và thỏa mãn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 1\). Hãy chọn mệnh đề đúng trong các mệnh đề sau:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = 1\) nên y = 1 là đường TCN của đồ thị hàm số \(y = f\left( x \right)\)
Hàm số \(y = - {x^3} + 3x - 5\) đồng biến trên khoảng nào?
TXD: D = R
\(\begin{array}{l}y' = - 3{x^2} + 3\\y' = 0 \Leftrightarrow - 3{x^2} + 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\end{array}\)
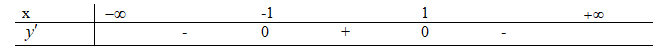
Đồng biến trên (-1,1).
Trong các hàm số sau, hàm số nào luôn nghịch biến trên R?
Đáp án A: \(y' = \cos x - 1 \le 0,\forall x \in \mathbb{R}\) vì \(\cos x \le 1\) với mọi \(x \in \mathbb{R}\)
Vậy hàm số \(y = \sin x - x\) luôn nghịch biến trên \(\mathbb{R}\)
Cho hàm số \(y = {x^4} - 4{x^2} + 3\). Mệnh đề nào dưới đây sai?
Ta có:
\(y' = 4{x^3} - 8x = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \end{array} \right.\)
Do đó hàm số có 3 điểm cực trị nên A sai.
Với a, b là các số dương. Tính giá trị biểu thức \({{{a^{{1 \over 3}}}\sqrt b + {b^{{1 \over 3}}}\sqrt a } \over {\root 6 \of a + \root 6 \of b }}\)
Ta có: \(\dfrac{{{a^{\dfrac{1}{3}}}\sqrt b + {b^{\dfrac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}} \)
\(= \dfrac{{{a^{\dfrac{1}{3}}}{b^{\dfrac{1}{2}}} + {b^{\dfrac{1}{3}}}{a^{\dfrac{1}{2}}}}}{{{a^{\dfrac{1}{6}}} + {b^{\dfrac{1}{6}}}}} \)
\(= \dfrac{{{a^{\dfrac{1}{3}}}{b^{\dfrac{1}{3}}}\left( {{a^{\dfrac{1}{6}}} + {b^{\dfrac{1}{6}}}} \right)}}{{{a^{\dfrac{1}{6}}} + {b^{\dfrac{1}{6}}}}}\)
\(= {a^{\dfrac{1}{3}}}{b^{\dfrac{1}{3}}} = \sqrt[3]{{ab}}\)
Tìm nghiệm của bất phương trình \({(8,5)^{{{x - 3} \over {{x^2} + 1}}}} < 1\)
Ta có: \({(8,5)^{\dfrac{{x - 3}}{{{x^2} + 1}}}} < 1\)
\(\Leftrightarrow \dfrac{{x - 3}}{{{x^2} + 1}} < 0\)
\(\Leftrightarrow x - 3 < 0 \Leftrightarrow x < 3\)
Cho \(c = {\log _{15}}3.\) Khi đó giá trị của \({\log _{25}}15\) theo c là
Ta có: \(c = {\log _{15}}3\)
\(\Leftrightarrow \dfrac{1}{c} = {\log _3}15 = {\log _3}\left( {3.5} \right) = {\log _3}5 + 1\)
\(\Rightarrow {\log _3}5 = \dfrac{1}{c} - 1 = \dfrac{{1 - c}}{c}\)
\(\Leftrightarrow {\log _5}3 = \dfrac{c}{{1 - c}}\)
Khi đó ta có:
\({\log _{25}}15 = \dfrac{1}{2}{\log _5}\left( {3.5} \right)\)
\(= \dfrac{1}{2}\left( {1 + {{\log }_5}3} \right)\)
\(= \dfrac{1}{2}\left( {1 + \dfrac{c}{{1 - c}}} \right)\)
\(= \dfrac{1}{{2\left( {1 - c} \right)}}\)
Cho \(a = {\log _3}15\,,\,\,b = {\log _3}10\). Tính giá trị của \({\log _{\sqrt 3 }}50\) theo a và b.
Ta có: \({\log _{\sqrt 3 }}50 = 2{\log _3}50 \)\(\,= 2\left( {{{\log }_3}5 + {{\log }_3}10} \right)\)
Mà \(a = {\log _3}15 = {\log _3}\left( {3.5} \right) = 1 + {\log _3}5\)\(\, \Rightarrow {\log _3}5 = a - 1\)
Khi đó \({\log _{\sqrt 3 }}50 = 2\left( {a - 1 + b} \right) = 2a + 2b - 2\)
Với 0 < a < b, \(m \in {N^*}\) thì:
Với 0 < a < b, \(m \in {N^*}\) ta có \({a^m} < {b^m}\)
Nếu n chẵn thì điều kiện để \(\root n \of b \) có nghĩa là:
Với n chẵn thì điều kiện để \(\sqrt[n]{b}\) có nghĩa là \(b \ge 0\)
Chọn mệnh đề đúng
Ta có:
+ \(\left\{ {\begin{array}{*{20}{l}}{{2^{{{\log }_2}3}} = 3}\\{0 < {{\log }_5}3 < {{\log }_3}5 \Rightarrow {5^{{{\log }_3}5}} > {5^{{{\log }_5}3}} = 3}\end{array}} \right. \to \) Đáp án A sai.
+ \(\left\{ \begin{array}{l}{2^{{{\log }_2}3}} = 3\\{5^{{{\log }_5}3}} = 3\end{array} \right. \to \) Đáp án B đúng.
Cho a, b là các số thực dương, thỏa mãn \({a^{{3 \over 4}}} > {a^{{4 \over 5}\,\,\,}}\,\,,\,\,\,{\log _b}{1 \over 2} < {\log _b}{2 \over 3}\). Mệnh đề nào sau đây đúng?
Ta có:
\({a^{\dfrac{3}{4}}} > {a^{\dfrac{4}{5}\,\,\,}}\,\, \Rightarrow 0 < a < 1\,\); \(\,\,{\log _b}\dfrac{1}{2} < {\log _b}\dfrac{2}{3} \Rightarrow b > 1\)
Bất phương trình \({\log _{{1 \over 3}}}{\log _4}({x^2} - 5) > 0\) có tập nghiệm là bao nhiêu?
Điều kiện: \({x^2} - 5 > 0\)
Ta có: \({\log _{\dfrac{1}{3}}}{\log _4}({x^2} - 5) > 0\)
\(\Leftrightarrow 0 < {\log _4}({x^2} - 5) < 1\)
\(\Leftrightarrow \left\{ \begin{array}{l}{x^2} - 5 < 4\\{x^2} - 5 > 1\end{array} \right. \)
\(\Leftrightarrow \)\(x \in ( - 3; - \sqrt 6 ) \cup (\sqrt 6 ;3)\)
Nếu x > y > 0 thì \({{{x^y}{y^x}} \over {{y^y}{x^x}}}\) bằng giá trị nào?
Ta có:
\(\dfrac{{{x^y}{y^x}}}{{{y^y}{x^x}}} = {\left( {\dfrac{x}{y}} \right)^y}.{\left( {\dfrac{y}{x}} \right)^x}\)\(\, = {\left( {\dfrac{x}{y}} \right)^y}{\left( {\dfrac{x}{y}} \right)^{ - x}} = {\left( {\dfrac{x}{y}} \right)^{y - x}}\)
Hình tứ diện đều có mấy mặt phẳng đối xứng?
Tứ diện đều có mặt phẳng đối xứng là mặt phẳng đi qua 1 cạnh và trung điểm cạnh đối diện. Vì tứ diện đều có 6 cạnh nên có 6 mặt phẳng đối xứng.
Trong các mệnh đề sau, mệnh đề nào sai?
Các hình tứ diện đều, lập phương, bát diện đều là các khối đa diện đều nên chúng là đa diện lồi.
Hình tạo bởi hai tứ diện đều ghép với nhau có thể là đa diện lồi hoặc không phải là đa diện lồi
⇒ Mệnh đề “Hình tạo bởi hai tứ diện đều ghép với nhau là đa diện lồi” là mệnh đề sai
Khối mười hai mặt đều là khối đa diện đều loại nào?
Khối mười hai mặt đều thuộc loại \(\left\{ {5;3} \right\}\).
Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính diện tích xung quanh của hình trụ.
Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông
Diện tích xung quanh của hình trụ là \(4\pi {a^2}\)
Phép vị tự tỉ số k > 0 biến khối chóp có thể tích V thành khối chóp có thể tích V'. Khi đó:
Phép vị tự tỉ số k > 0 biến khối chóp có thể tích V thành khối chóp có thể tích V'. Khi đó \(\dfrac{{V'}}{V} = {k^3}\).
Cho hai điểm A, B cố định. Tập hợp các điểm M trong không gian sao cho diện tích tam giác MAB không đổi là
Gọi d là khoảng cách từ điểm M đến đường thẳng AB.
Suy ra \({S_{MAB}} = \dfrac{1}{2}.d\left( {M,AB} \right).AB = \dfrac{1}{2}d.AB\)
Vì \({S_{MAB}};AB\) là hằng số nên d không đổi .
Vậy tập hợp các điểm M thỏa mãn yêu cầu bài toán là một mặt trụ tròn xoay.
Một hình trụ \(\left( H \right)\) có diện tích xung quanh bằng \(4\pi\). Biết thiết diện của \(\left( H \right)\) qua trục là hình vuông. Diện tích toàn phần của \(\left( H \right)\) bằng
Gọi a là chiều cao của khối trụ suy ra khối trụ có bán kính bằng \(\dfrac{a}{2}\)
Ta có: \({S_{xq}} = 2\pi .\dfrac{a}{2}.a = 4\pi \Leftrightarrow a = 2\)
Diện tích toàn phần của khối trụ là: \({S_{tp}} = {S_{xq}} + 2.{S_d} = 4\pi + 2.\pi {.1^2} = 6\pi\)
Người ta bỏ bốn quả bóng bàn cùng kích thước, bán kính bằng a vào trong một chiếc hộp hình trụ có đáy bằng hỉnh tròn lớn của quả bóng bàn. Biết quả bóng nằm dưới cùng, quả bóng nằm trên cùng lần lượt tiếp xúc với mặt đáy dưới và mặt đáy trên của hình trụ đó. Lúc đó, diện tích xung quanh của hình trụ bằng
Chiều cao hình trụ \(h = 4d = 4.2r = 8a\)
Bán kính đáy hình trụ là R = a
Diện tích xung quanh của khối trụ là:
\({S_{xq}} = 2\pi Rh = 2\pi .a.8a = 16\pi {a^2}\)
Trong số các mệnh đề sau, mệnh đề nào đúng?
Tồn tại duy nhất một mặt cầu đi qua hai đường tròn cắt nhau nằm trong hai mặt phẳng phân biệt.
Chọn đáp án D
Cho hình trụ có bán kính đáy bằng \(3{\rm{ cm}}\), trục \(OO' = 8{\rm{ cm}}\) và mặt cầu đường kính \(OO'\). Hiệu số giữa diện tích mặt cầu và diện tích xung quanh hình trụ là bao nhiêu?
Diện tích mặt cầu có đường kính OO’ = 8 cm là:
\({S_c} = 4\pi {R^2} = 4\pi {.4^2} = 64\pi \,\left( {c{m^2}} \right)\)
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .3.8 = 48\pi \left( {c{m^2}} \right)\)
Hiệu số giữa diện tích mặt cầu và diện tích xung quanh hình trụ là:
\(64\pi - 48\pi = 16\pi \left( {c{m^2}} \right)\)

