Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Lý Tự Trọng
Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Lý Tự Trọng
-
Hocon247
-
30 câu hỏi
-
60 phút
-
232 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Gọi M, N là giao điểm của đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) và đường thẳng d: y = x + 2. Hoành độ trung điểm I của đoạn MN là bao nhiêu?
Xét pt:
\(\begin{array}{l}\dfrac{{x + 1}}{{x - 2}} = x + 2{\rm{ }}\left( {{\rm{Dk: x}} \ne {\rm{2 }}} \right)\\ \Rightarrow x + 1 = {x^2} - 4\\ \Leftrightarrow {x^2} - x - 5 = 0\\ \Rightarrow \left[ \begin{array}{l}{x_M} = \dfrac{{1 + \sqrt {21} }}{2}\\{x_N} = \dfrac{{1 - \sqrt {21} }}{2}\end{array} \right.\end{array}\)
Do I là trung điểm của MN nên \({x_I} = \frac{{{x_M} + {x_N}}}{2} = \frac{{\frac{{1 + \sqrt {21} }}{2} + \frac{{1 - \sqrt {21} }}{2}}}{2}= \dfrac{1}{2}\)
Tâm đối xứng của đồ thị hàm số nào sau đây cách gốc tọa độ một khoảng lớn nhất?
Đáp án A: tâm đối xứng \(I\left( { - 3;2} \right)\) \( \Rightarrow OI = \sqrt {{{\left( { - 3} \right)}^2} + {2^2}} = \sqrt {13} \)
Đáp án B: tâm đối xứng \(I\left( { - 1; - 1} \right)\) \( \Rightarrow OI = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 \)
Đáp án C:
\(\begin{array}{l}y' = 6{x^2} - 6x\\y'' = 12x - 6 = 0 \Leftrightarrow x = \frac{1}{2}\\ \Rightarrow y\left( {\frac{1}{2}} \right) = - \frac{5}{2}\end{array}\)
tâm đối xứng \(I\left( {\frac{1}{2};\frac{5}{2}} \right)\) \( \Rightarrow OI = \sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2}} = \frac{{\sqrt {26} }}{2}\)
Đáp án D:
\(\begin{array}{l}y' = - 3{x^2} + 3\\y'' = - 6x = 0 \Leftrightarrow x = 0\\ \Rightarrow y\left( 0 \right) = - 2\end{array}\)
tâm đối xứng \(I\left( {0; - 2} \right)\) \( \Rightarrow OI = \sqrt {{0^2} + {{\left( { - 2} \right)}^2}} = 2\)
Vậy điểm cách O khoảng lớn nhất là \(I\left( { - 3;2} \right)\).
Chọn đáp án A.
Cho hàm số \(f(x) = {x^3} + a{x^2} + bx + c\). Mệnh đề nào sau đây sai?
C sai vì có thể xảy ra TH hàm số đơn điệu trên R nên không có cực trị.
Cho hàm số \(y = \dfrac{{x - 1} }{ {x + 2}}\) có đồ thị (C). Tiếp tuyến của (C) tại giao điểm của (C) với trục hoành có phương trình là:
\(y = \dfrac{{x - 1}}{{x + 2}}\)
TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\)
Xét pt hoành độ: \(\dfrac{{x - 1}}{{x + 2}} = 0 \Leftrightarrow x - 1 = 0 \Leftrightarrow x = 1\)
\(\begin{array}{l}y' = \dfrac{3}{{{{(x + 2)}^2}}}\\ \Rightarrow y'\left( 1 \right) = \dfrac{1}{3}\end{array}\)
Vậy pt tiếp tuyến của ( C) tại giao điểm của c với trục hoành: \(y = \dfrac{1}{3}\left( {x - 1} \right)\)
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây.
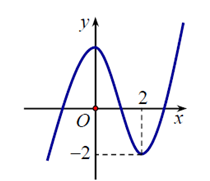
Mệnh đề nào dưới đây đúng?
Hàm số có giá trị cực tiểu \(y = - 2\) nên A sai.
Hàm số đạt cực tiểu tại \(x = 2\) và đạt cực đại tại \(x = 0\) nên B đúng.
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{2x}}{{x - 2}}\).
Đồ thị hàm số \(y = \frac{{2x}}{{x - 2}}\) có đường TCN là \(y = 2\) hay \(y - 2 = 0\).
Cho hàm số \(y = \dfrac{1 }{ 4}{x^4} - 2{x^2} + 3\). Khẳng định nào sau đây đúng?
\(y = \dfrac{1}{4}{x^4} - 2{x^2} + 3\)
TXĐ: \(D = \mathbb{R}\)
\(\begin{array}{l}y' = {x^3} - 4x\\y' = 0 \Rightarrow {x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\\x = 2\end{array} \right.\end{array}\)

Từ BBT, hàm số ĐB trên \(\left( { - 2,0} \right)\)và \({\rm{(2, + }}\infty {\rm{)}}\); NB trên \(( - \infty , - 2)\) và \(\left( {0,2} \right)\)
Đồ thị sau đây là của hàm số nào?
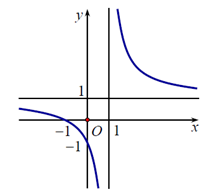
TCĐ: \(x = 1\) loại C.
Đths đi qua điểm \(\left( { - 1;0} \right)\) nên loại A,B.
Tìm giá trị lớn nhất của hàm số \(y = \dfrac{{3x - 1}}{ {x - 3}}\) trên đoạn [0 ; 2]
\(y' = - \frac{8}{{{{\left( {x - 3} \right)}^2}}} < 0\) nên hàm số nghịch biến trên \(\left[ {0;2} \right]\)
\( \Rightarrow \mathop {\max }\limits_{\left[ {0;2} \right]} y = y\left( 0 \right) = \frac{1}{3}\)
Hàm số \(y =\dfrac {1 }{ 3}{x^3} - 2{x^2} + 3x - 1\) nghịch biến trên khoảng nào trong những khoảng sau đây?
\(y = \dfrac{1}{3}{x^3} - 2{x^2} + 3x - 1\)
\(\begin{array}{l}
y' = {x^2} - 4x + 3\\
y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x = 3
\end{array} \right.
\end{array}\)
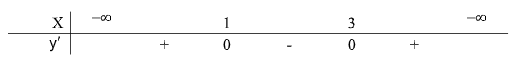
Vậy hàm số nghịch biến trên (1,3).
Hàm số \(y = \sqrt {{x^2} + 3x + 5} \). Tính y’(1) được:
Ta có: \(y = \sqrt {{x^2} + 3x + 5} \)
\(\Rightarrow y' = {\left( {\sqrt {{x^2} + 3x + 5} } \right)^\prime } \)\(\,= \dfrac{{{{\left( {{x^2} + 3x + 5} \right)}^\prime }}}{{2\sqrt {{x^2} + 3x + 5} }}\)\(\; = \dfrac{{2x + 3}}{{2\sqrt {{x^2} + 3x + 5} }}\)
Khi đó \(y'\left( 1 \right) = \dfrac{{2.1 + 3}}{{2\sqrt {1 + 3.1 + 5} }} = \dfrac{5}{{2.3}} = \dfrac{5}{6}\).
Cho \(m \in N*\),chọn kết luận đúng:
Ta có: \(\dfrac{5}{4} > \dfrac{6}{5} > 1 \Rightarrow {\left( {\dfrac{5}{4}} \right)^m} > {\left( {\dfrac{6}{5}} \right)^m} > 1,\,\forall m \in {\mathbb{N}^ * }\)
Cho số nguyên dương \(n \ge 2\), số a được gọi là căn bậc n của số thực b nếu:
Số a được gọi là căn bậc n của số b khi \({a^n} = b\)
Chọn mệnh đề sai:
Ta có:
+ \({\log _a}{a^b} = b{\log _a}a = b.1 = b\)
+ \({a^{{{\log }_a}b}} = b\) khi đó \({a^{{{\log }_a}b}} = {\log _a}{a^b}\)
Trong các khẳng định dưới đây, khẳng định nào sai?
Các khẳng định đúng:
+ \({\log _2}x > 0\,\, \Leftrightarrow \,\,\,x > 1\)
+ \({\log _{\dfrac{1}{3}}}a = {\log _{\dfrac{1}{3}}}b\,\,\, \Leftrightarrow \,\,a = b > 0\,\)
+ \(\log x < 0\,\,\, \Leftrightarrow \,\,\,0 < x < 1\)
Bất phương trình mũ \({1 \over {{3^x} + 5}} \le {1 \over {{3^{x + 1}} - 1}}\) có tập nghiệm là bao nhiêu?
Điều kiện \(x \ne - 1\)
Ta có: \(\dfrac{1}{{{3^x} + 5}} \le \dfrac{1}{{{3^{x + 1}} - 1}}\)
\(\Leftrightarrow \dfrac{1}{{{3^x} + 5}} - \dfrac{1}{{{3^{x + 1}} - 1}} \le 0\)
\( \Leftrightarrow \dfrac{{{{3.3}^x} - 1 - {3^x} - 5}}{{\left( {{3^x} + 5} \right)\left( {{3^{x + 1}} - 1} \right)}} \le 0\)
\(\Leftrightarrow \dfrac{{{{2.3}^x} - 6}}{{\left( {{3^x} + 5} \right)\left( {{3^{x + 1}} - 1} \right)}} \le 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{2.3^x} - 6 \le 0\\{3^{x + 1}} - 1 > 0\end{array} \right.\\\left\{ \begin{array}{l}{2.3^x} - 6 \ge 0\\{3^{x + 1}} - 1 < 0\end{array} \right.\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \le 1\\x > - 1\end{array} \right.\\\left\{ \begin{array}{l}x \ge 1\\x < - 1\end{array} \right.\end{array} \right. \Rightarrow x \in \left( { - 1;1} \right]\)
Rút gọn biểu thức \(P = {{{a^2}b.{{(a{b^{ - 2}})}^{ - 3}}} \over {{{({a^{ - 2}}{b^{ - 1}})}^{ - 2}}}}\)
Ta có: \(P = \dfrac{{{a^2}b.{{(a{b^{ - 2}})}^{ - 3}}}}{{{{({a^{ - 2}}{b^{ - 1}})}^{ - 2}}}} = \dfrac{{{a^{ - 1}}{b^7}}}{{{a^4}{b^2}}} \)\(\,= {a^{ - 5}}{b^5} = {\left( {\dfrac{b}{a}} \right)^5}\)
Cho hàm số \(y = {x^{{1 \over 4}}}(10 - x)\,,\,\,x > 0\). Khẳng định nào sau đây là đúng?
Ta có: \(y = {x^{\dfrac{1}{4}}}(10 - x)\,,\,\,x > 0\)
\(\Rightarrow y' = \dfrac{1}{4}{x^{ - \dfrac{3}{4}}}\left( {10 - x} \right) - {x^{\dfrac{1}{4}}}\)\(\, = \dfrac{{10 - x}}{{4\sqrt[4]{{{x^3}}}}} - \dfrac{1}{{\sqrt[4]{x}}} \)\(\,= \dfrac{1}{{\sqrt[4]{x}}}\left( {\dfrac{{10 - x}}{{4\sqrt x }} - 1} \right)\)
+) \(y' = 0 \Leftrightarrow \dfrac{1}{{\sqrt[4]{x}}}\left( {\dfrac{{10 - x}}{{4\sqrt x }} - 1} \right) = 0 \)
\(\Leftrightarrow \dfrac{{10 - x}}{{4\sqrt x }} - 1 = 0 \Leftrightarrow 10 - x = 4\sqrt x \)
\( \Leftrightarrow x + 4\sqrt x - 10 = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}\sqrt x = - 2 + \sqrt {14}(tm) \\\sqrt x = - 2 - \sqrt {14}(ktm) \end{array} \right.\)
\( \Leftrightarrow x = 18 - 4\sqrt {14} \)
+ Hàm số đồng biến trên \(\left( {0; 18 -4\sqrt {14} } \right)\) và nghịch biến trên \(\left( { 18- 4\sqrt {14} ; + \infty } \right)\)
Rút gọn biểu thức \(p = \log {a \over b} + \log {b \over c} + \log {c \over d} - \log {{ay} \over {dx}}\)
Ta có: \(p = \log \dfrac{a}{b} + \log \dfrac{b}{c} + \log \dfrac{c}{d} - \log \dfrac{{ay}}{{dx}} \)
\(= \log \left( {\dfrac{{abc}}{{bcd}}} \right) - \left( {\log \dfrac{a}{d} + \log \dfrac{y}{x}} \right)\)
\( = \log \left( {\dfrac{a}{d}} \right) - \left( {\log \dfrac{a}{d} + \log \dfrac{y}{x}} \right) \)
\(= - \log \dfrac{y}{x} = \log \dfrac{x}{y}.\)
Cho b > 1, sinx > 0, cosx > 0 và \({\log _b}\sin x = a\) Khi đó \({\log _b}\cos x\) bằng bao nhiêu?
Ta có \({\log _b}\sin x = a \Rightarrow \sin x = {b^a} \)
\(\Leftrightarrow {\sin ^2}x = {\left( {{b^a}} \right)^2}\)
\( \Rightarrow {\cos ^2}x = 1 - {\sin ^2}x = 1 - {\left( {{b^a}} \right)^2}\)
\(\Leftrightarrow \cos x = \sqrt {1 - {{\left( {{b^a}} \right)}^2}} \)
Khi đó \({\log _b}\cos x = {\log _b}{\left( {1 - {{\left( {{b^a}} \right)}^2}} \right)^{\dfrac{1}{2}}}\)\(\, = \dfrac{1}{2}{\log _b}\left( {1 - {{\left( {{b^a}} \right)}^2}} \right)\)
Công thức tính thể tích của khối chóp có diện tích đáy B và chiều cao h
Công thức tính thể tích của khối chóp có diện tích đáy B và chiều cao h là \(V = \dfrac{1}{3}Bh.\)
Có bao nhiêu loại khối đa diện đều?
Có 5 khối đa diện đều.
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA = a. Tính thể tích V của khối chóp đã cho.
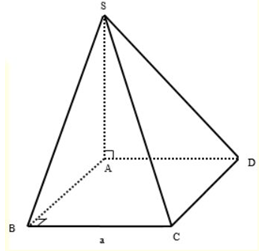
\(\begin{array}{l}{S_{ABCD}} = {a^2}\\{V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \dfrac{1}{3}a.{a^2} = \dfrac{{{a^3}}}{3}\end{array}\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. SA vuông góc với đáy; góc tạo bởi SC và (SAB) là 300 . Gọi E, F là trung điểm của BC và SD. Tính khoảng cách giữa hai đường thẳng chéo nhau DE và CF.
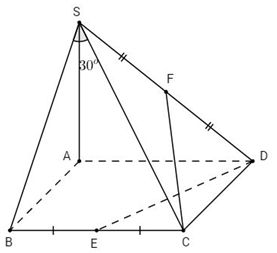
Góc giữa SC và (SAB) là góc BSC
\( \Rightarrow \widehat {BSC} = {30^o}\)
\(\begin{array}{l}SB = CB\cot {30^o} = a\sqrt 3 \\SA = \sqrt {S{B^2} - A{B^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \end{array}\)
Gắn hệ trục tọa độ như sau:
Gốc \(O \equiv A\left( {0;0;0} \right);\,Ox \equiv AB;\)
\(\,Oy \equiv AD;\,Oz \equiv AS\)
Tạo độ các điểm được xác định như sau:
\(\begin{array}{l}D\left( {0;a;0} \right);E\left( {a;\dfrac{a}{2};0} \right);C\left( {a;a;0} \right);F\left( {0;\dfrac{a}{2};\dfrac{a}{{\sqrt 2 }}} \right)\\\overrightarrow {DE} \left( {a; - \dfrac{a}{2};0} \right)\\\overrightarrow {CF} \left( { - a; - \dfrac{a}{2};\dfrac{a}{{\sqrt 2 }}} \right)\\\overrightarrow {DC} \left( {a;0;0} \right)\\\left[ {\overrightarrow {DE} ,\overrightarrow {CF} } \right] = \left( { - \dfrac{{{a^2}}}{{2\sqrt 2 }}, - \dfrac{{{a^2}}}{{\sqrt 2 }}; - {a^2}} \right)\\d = \dfrac{{\left| {\overrightarrow {DC} .\left[ {\overrightarrow {DE} ,\overrightarrow {CF} } \right]} \right|}}{{\left| {\left[ {\overrightarrow {DE} ,\overrightarrow {CF} } \right]} \right|}}\\\,\,\,\,\,\,\, = \dfrac{{\left| { - \dfrac{{{a^3}}}{{2\sqrt 2 }}} \right|}}{{\sqrt {{{\left( { - \dfrac{{{a^2}}}{{2\sqrt 2 }}} \right)}^2} + {{\left( { - \dfrac{{{a^2}}}{{\sqrt 2 }}} \right)}^2} + {{\left( { - {a^2}} \right)}^2}} }}\\\,\,\,\,\,\, = \dfrac{{a\sqrt {13} }}{{13}}\end{array}\)
Chọn khẳng định đúng trong các khẳng định sau:
Hình bát diện đều là đa diện đều loại {3; 4}.
Cho khối chóp có 20 cạnh. Số mặt của khối chóp đó bằng bao nhiêu?
Giả sử dáy của hình chóp có n cạnh \( \Rightarrow 2n = 20 \Leftrightarrow n = 10\)
Do đó số mặt của chóp là: 10 + 1 = 11
Hình lập phương có bao nhiêu mặt phẳng đối xứng?
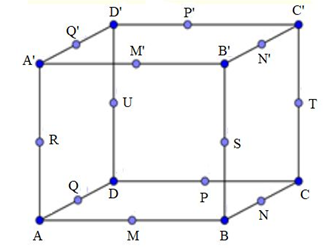
Xét khối lập phương ABCD.A'B'C'D'
Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA
M', N', P', Q' lần lượt là trung điểm của A'B', B'C', C'D', D'A'
R, S, T, U lần lượt là trung điểm của AA', BB', CC', DD'
Khối lập phương ABCD. A'B'C'D' có 9 mp đối xứng như sau:
a) 3 mp đối xứng chia nó thành 2 khối hộp chữ nhật (là các mp MPP'M', NQQ'N', RSTU)
b) 6 mp đối xứng chia nó thành 2 khối lăng trụ tam giác (là các mp ACC'A', BDD'B', AB'C'D, A'BCD', ABC'D', A'B'CD)
Thể tích khối bát diện đều có cạnh bằng a
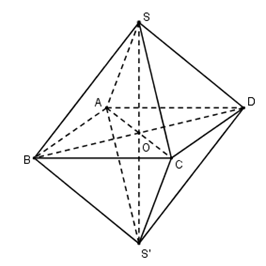
Thể tích khối bát diện đều \(V = 2{V_{S.ABCD}}\)
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\)
Vì ABCD là hình vuông nên \(AC = BD = a\sqrt 2 \)
\(\Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA\)
\(\Rightarrow \Delta SOA\) vuông tại O
\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} \)\(\, = \dfrac{{a\sqrt 2 }}{2}\)
\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} \)
\(= \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
\( \Rightarrow V = 2\dfrac{{{a^3}\sqrt 2 }}{6} = \dfrac{{{a^3}\sqrt 2 }}{3}\)
Khối đa diện đều loại {4; 3} có bao nhiêu đỉnh?
Lập phương loại {4;3} có M = 6 , Đ = 8
Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a
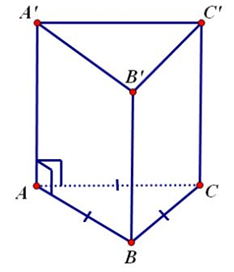
Thể tích khối lăng trụ tam giác đều có tất cả các cạnh a là:
\(V = \dfrac{{{a^2}\sqrt 3 }}{4}.a = \dfrac{{{a^3}\sqrt 3 }}{4}\)

