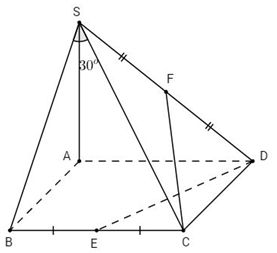
Góc giữa SC và (SAB) là góc BSC

\( \Rightarrow \widehat {BSC} = {30^o}\)

\(\begin{array}{l}SB = CB\cot {30^o} = a\sqrt 3 \\SA = \sqrt {S{B^2} - A{B^2}}  = \sqrt {3{a^2} - {a^2}}  = a\sqrt 2 \end{array}\)

Gắn hệ trục tọa độ như sau:

Gốc \(O \equiv A\left( {0;0;0} \right);\,Ox \equiv AB;\)

\(\,Oy \equiv AD;\,Oz \equiv AS\)

Tạo độ các điểm được xác định như sau:

\(\begin{array}{l}D\left( {0;a;0} \right);E\left( {a;\dfrac{a}{2};0} \right);C\left( {a;a;0} \right);F\left( {0;\dfrac{a}{2};\dfrac{a}{{\sqrt 2 }}} \right)\\\overrightarrow {DE} \left( {a; - \dfrac{a}{2};0} \right)\\\overrightarrow {CF} \left( { - a; - \dfrac{a}{2};\dfrac{a}{{\sqrt 2 }}} \right)\\\overrightarrow {DC} \left( {a;0;0} \right)\\\left[ {\overrightarrow {DE} ,\overrightarrow {CF} } \right] = \left( { - \dfrac{{{a^2}}}{{2\sqrt 2 }}, - \dfrac{{{a^2}}}{{\sqrt 2 }}; - {a^2}} \right)\\d = \dfrac{{\left| {\overrightarrow {DC} .\left[ {\overrightarrow {DE} ,\overrightarrow {CF} } \right]} \right|}}{{\left| {\left[ {\overrightarrow {DE} ,\overrightarrow {CF} } \right]} \right|}}\\\,\,\,\,\,\,\, = \dfrac{{\left| { - \dfrac{{{a^3}}}{{2\sqrt 2 }}} \right|}}{{\sqrt {{{\left( { - \dfrac{{{a^2}}}{{2\sqrt 2 }}} \right)}^2} + {{\left( { - \dfrac{{{a^2}}}{{\sqrt 2 }}} \right)}^2} + {{\left( { - {a^2}} \right)}^2}} }}\\\,\,\,\,\,\, = \dfrac{{a\sqrt {13} }}{{13}}\end{array}\)