Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng a. Gọi M là trung điểm của \(AA_1\). Thể tích khối chóp \(M.BC{A_1}\) là:
A. \(\dfrac{{{a^3}\sqrt 3 }}{{12}}\)
B. \(\dfrac{{{a^3}\sqrt 3 }}{{24}}\)
C. \(dfrac{{{a^3}\sqrt 3 }}{6}\)
D. \(\dfrac{{{a^3}\sqrt 3 }}{8}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
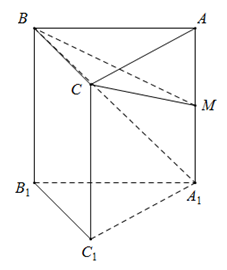
\(\Delta ABC\)là tam giác đều cạnh \(a\)nên có diện tích \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Ta có \(AM = \dfrac{{A{A_1}}}{2} = \dfrac{a}{2}\)
Hai tứ diện \(MABC\)và \(M{A_1}BC\)có chung đỉnh\(C\), diện tích hai đáy \(MAB\)và \(M{A_1}B\)bằng nhau nên có thể tích bằng nhau, suy ra
\({V_{M.BC{A_1}}} = {V_{M.ABC}} = \dfrac{1}{3}AM.{S_{ABC}} \)\(\,= \dfrac{{{a^3}\sqrt 3 }}{{24}}\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho lăng trụ tam giác ABC.A’B’C’ có thể tích là V, khi đó thể tích của khối chóp A’.ABC là
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh \(SA = SB = SC = \dfrac{{a\sqrt 6 }}{3}\). Tính thể tích V của khối chóp đã cho.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA vuông góc với (ABC). Tính khoảng cách từ trọng tâm G của tam giác SAB đến (SAC)?
Số nghiệm của phương trình \({\log _5}(5x) - {\log _{25}}(5x) - 3 = 0\) là:
Trong các hàm số sau đây, hàm số nào đồng biến trên R?
Một chiếc xe ô tô có thùng đựng hàng hình hộp chữ nhật với kích thước 3 chiều lần lượt là 2m; 1,5m; 0,7m. Tính thể tích thùng đựng hàng của xe ôtô đó.
Công thức tính thể tích của khối lăng trụ có diện tích đáy B và chiều cao h
Cho hàm số y = f(x) có bảng biến thiên như dưới đây.
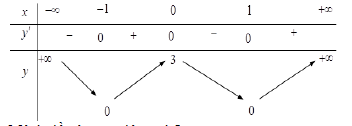
Mệnh đề nào sau đây sai?
Cho hàm số \(y = {x^3} - 3x\). Mệnh đề nào dưới đây đúng?
Cho hàm số y = f(x) có bảng biến thiên như sau:
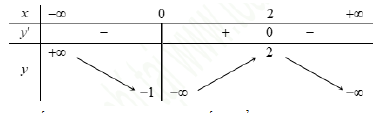
Tập tất cả các giá trị của tham số m để phương trình f(x) + m= 0 có ba nghiệm phân biệt là:
Khi tăng kích thước mỗi cạnh của khối hộp chữ nhật lên 5 lần thì thể tích khối hộp chữ nhật tăng bao nhiêu lần?
Điều kiện của tham số m đề hàm số \(y = \dfrac{{ - {x^3}}}{ 3} + {x^2} + mx\) nghịch biến trên R là

