Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Nguyễn Trung Trực
Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Nguyễn Trung Trực
-
Hocon247
-
30 câu hỏi
-
60 phút
-
241 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Hàm số \(y = - {x^3} + 3{x^2} - 4\) có đồ thị như hình vẽ sau
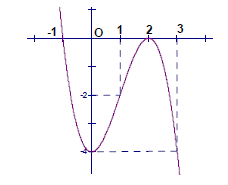
Tìm các giá trị của m đề phương trình \({x^3} - 3{x^2} + m = 0\) có hai nghiệm
\(\begin{array}{l}{x^3} - 3{x^2} + m = 0\\ \Leftrightarrow - {x^3} + 3{x^2} = m\\ \Leftrightarrow - {x^3} + 3{x^2} - 4 = m - 4\end{array}\)
Số nghiệm của phương trình \({x^3} - 3{x^2} + m = 0\) là số giao điểm của đồ thị hàm số \(y = - {x^3} + 3{x^2} - 4\) và đường thẳng \(y= m - 4\).
\( \Rightarrow \) Để pt \({x^3} - 3{x^2} + m = 0\) có 2 nghiệm phân biệt thì đồ thị hàm số \(y = - {x^3} + 3{x^2} - 4\) cắt đường thẳng \(y= m – 4\) tại 2 đi ểm \(\left[ \begin{array}{l}m - 4 = 0\\m - 4 = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 4\\m = 0\end{array} \right.\)
Điểm cực đại của hàm số \(y = - {x^3} + 3{x^2} + 2\)
\(y = - {x^3} + 3{x^2} + 2\)
TX Đ: \(D = \mathbb{R}\)
\(\begin{array}{l}y' = - 3{x^2} + 6x\\y' = 0\\ \Rightarrow - 3{x^2} + 6x = 0\\ \Leftrightarrow x( - 3x + 6) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\end{array}\)
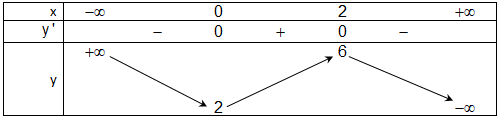
Từ bảng biến thiên, điểm cực đại của hàm số: \(x=2\)
Tìm số giao điểm của đồ thị hàm số \(y = {x^4} - 3{x^2} - 5\) và trục hoành.
Xét \(y = {x^4} - 3{x^2} - 5\)
TXĐ: \(D = \mathbb{R}\)
\(\begin{array}{l}y' = 4{x^3} - 6x\\y' = 0\\ \Rightarrow 4{x^3} - 6x = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{{\sqrt 6 }}{2}\\x = - \dfrac{{\sqrt 6 }}{2}\end{array} \right.\end{array}\)
Bảng biến thiên
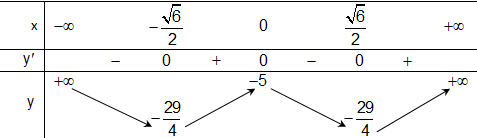
Từ bảng biến thiên, số giao điểm của đồ thị \(y = {x^4} - 3{x^2} - 5\) với trục hoành là 2.
Cho hàm số \(y = {x^3} - 2x + 1\) có đồ thị (C). Hệ số góc tiếp tuyến với (C) tại điểm M(- 1 ; 2) bằng:
\(\begin{array}{l}
y' = 3{x^2} - 2\\
\Rightarrow k = y'\left( { - 1} \right) = 3.{\left( { - 1} \right)^2} - 2 = 1
\end{array}\)
Điều kiện của tham số m đề hàm số \(y = \dfrac{{ - {x^3}}}{ 3} + {x^2} + mx\) nghịch biến trên R là
\(y = - \dfrac{{{x^3}}}{3} + {x^2} + mx\)
Txđ : \(D = \mathbb{R}\)
\(y' = - {x^2} + 2x + m\)
Hàm số \(y = - \dfrac{{{x^3}}}{3} + {x^2} + mx\) nghịch biến trên \(\mathbb{R}\)
\(\begin{array}{l} \Leftrightarrow y' \le 0\;\forall x \in \mathbb{R}\\ \Leftrightarrow - {x^2} + 2x + m \le 0\;\forall x \in \mathbb{R}\\ \Leftrightarrow \Delta ' \le 0\;\forall x \in \mathbb{R}\\ \Leftrightarrow 1 + m \le 0\;\forall x \in \mathbb{R}\\ \Leftrightarrow m \le - 1\end{array}\)
Đồ thị hàm số \(y = \dfrac{{2x - 3} }{{x - 1}}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là
\(y = \dfrac{{2x - 3}}{{x - 1}}\)
TXĐ : D=\(\mathbb{R}\backslash \left\{ 1 \right\}\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{2x - 3}}{{x - 1}} = 2\\ \Rightarrow TCN:y = 2\\\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \\\mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \end{array} \right\} \Rightarrow TCĐ:x = 1\end{array}\)
Cho hàm số \(y = {x^3} - 3x\). Mệnh đề nào dưới đây đúng?
y=x3 – 3x
TXĐ: \(D = \mathbb{R}\)
\(\begin{array}{l}y' = 3{x^2} - 3\\y' = 0\\ \Rightarrow 3{x^2} - 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\end{array} \right.\end{array}\)
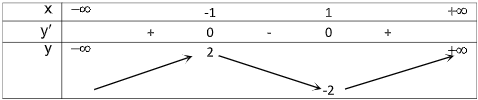
Từ bảng biến thiên, hàm số đồng biến trên \(( - \infty , - 1)\) và \((1, + \infty )\); nghịch biến trên \(( - 1,1)\)
Trong các hàm số sau đây, hàm số nào đồng biến trên R?
\(y = {x^3} + 1\)
TXĐ: \(D = \mathbb{R}\)
\(\begin{array}{l}y' = 3{x^2}\\y' = 0 \Rightarrow 3{x^2} = 0 \Rightarrow x = 0\end{array}\)
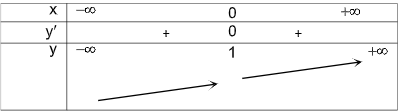
Từ bbt, hàm số đồng biến trên \(\mathbb{R}\)
Cho hàm số y = f(x) có bảng biến thiên như dưới đây.
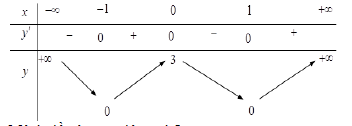
Mệnh đề nào sau đây sai?
Hàm số có ba điểm cực trị. (Đúng)
Hàm số có giá trị cực đại bằng 3. (Đúng)
Hàm số có giá trị cực đại bằng 0. (Sai vì Hàm số có giá trị cực tiểu bằng 0)
Hàm số có hai điểm cực tiểu. (Đúng)
Cho hàm số y = f(x) có bảng biến thiên như sau:
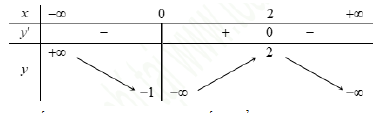
Tập tất cả các giá trị của tham số m để phương trình f(x) + m= 0 có ba nghiệm phân biệt là:
\(f\left( x \right) + m = 0 \Leftrightarrow f\left( x \right) = - m\)
Số nghiệm của phương trình \(\) chính bằng số giao điểm của đths y=f(x) và đường thẳng y= -m
Để \(f\left( x \right) + m = 0\) có 3 nghiệm pb thì đths y = f(x) cắt đường thẳng y=-m tại 3 điểm
\(\begin{array}{l} \Rightarrow - 1 < - m < 2\\ \Leftrightarrow - 2 < m < 1\\ \Rightarrow m \in \left( { - 2,1} \right)\end{array}\)
Cho số dương a, biểu thức \(\sqrt a .\root 3 \of a \root 6 \of {{a^5}} \) viết dưới dạng lũy thừa hữu tỷ là:
Ta có: \(\sqrt a .\sqrt[3]{a}\sqrt[6]{{{a^5}}} = {a^{\dfrac{1}{2}}}.\,{a^{\dfrac{1}{3}}}.\,{a^{\dfrac{5}{6}}}\)\(\, = {a^{\dfrac{1}{2} + \dfrac{1}{3} + \dfrac{5}{6}}} = {a^{\dfrac{5}{3}}}\)
Tìm tập xác định của hàm số sau \(f(x) = \sqrt {{{\log }_2}{\dfrac{3 - 2x - {x^2}}{x + 1}}} \).
Tập xác định của hàm số:
\(\left\{ \begin{array}{l}{\log _2}\dfrac{{3 - 2x - {x^2}}}{{x + 1}} \ge 0\\\dfrac{{3 - 2x - {x^2}}}{{x + 1}} > 0;\,x \ne - 1\end{array} \right. \\ \Leftrightarrow \dfrac{{3 - 2x - {x^2}}}{{x + 1}} \ge 1 \\ \Leftrightarrow \dfrac{{2 - 3x - {x^2}}}{{x + 1}} \ge 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2 - 3x - {x^2} \ge 0\\x + 1 > 0\end{array} \right.\\\left\{ \begin{array}{l}2 - 3x - {x^2} \le 0\\x + 1 < 0\end{array} \right.\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \in \left[ {\dfrac{{ - 3 - \sqrt {17} }}{2};\dfrac{{ - 3 + \sqrt {17} }}{2}} \right]\\x > - 1\end{array} \right.\\\left\{ \begin{array}{l}x \in \left( { - \infty ;\dfrac{{ - 3 - \sqrt {17} }}{2}} \right] \cup \left[ {\dfrac{{ - 3 + \sqrt {17} }}{2}; + \infty } \right)\\x < - 1\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x \in \left( { - 1;\dfrac{{ - 3 + \sqrt {17} }}{2}} \right]\\x \in \left( { - \infty ;\dfrac{{ - 3 - \sqrt {17} }}{2}} \right]\end{array} \right.\)
\( \Rightarrow \)\(\left( { - \infty ;\dfrac{{ - 3 - \sqrt {17} }}{2}} \right] \cup \left( { - 1;\dfrac{{ - 3 + \sqrt {17} }}{2}} \right]\)
Giá trị của \({\log _a}\left( {\dfrac{{a^2}\root 3 \of {{a^2}} \root 5 \of {{a^4}} }{{\root {15} \of {{a^7}} }}} \right)\) bằng:
Ta có:
\({\log _a}\left( {\dfrac{{{a^2}\sqrt[3]{{{a^2}}}\sqrt[5]{{{a^4}}}}}{{\sqrt[{15}]{{{a^7}}}}}} \right)\)
\(= {\log _a}\left( {\dfrac{{{a^2}.{a^{\dfrac{2}{3}}}.{a^{\dfrac{4}{5}}}}}{{{a^{\dfrac{7}{{15}}}}}}} \right)\)
\(= {\log _a}\left( {\dfrac{{{a^{\dfrac{{52}}{{15}}}}}}{{{a^{\dfrac{7}{{15}}}}}}} \right)\)
\(= {\log _a}\left( {{a^3}} \right) = 3\)
Cho \({4^x} + {4^{ - x}} = 23\). Khi đó biểu thức \(K = \dfrac{5 + {2^x} + {2^{ - x}}}{{1 - {2^x} - {2^{ - x}}}}\) có giá trị bằng:
Ta có: \({4^x} + {4^{ - x}} = 23 \)
\(\Leftrightarrow {\left( {{2^x}} \right)^2} + {\left( {{2^{ - x}}} \right)^2} = 23 \)
\(\Leftrightarrow {\left( {{2^x} + {2^{ - x}}} \right)^2} - {2.2^x}{.2^{ - x}} = 23\)
\( \Leftrightarrow {\left( {{2^x} + {2^{ - x}}} \right)^2} = 25\)
\(\Leftrightarrow {2^x} + {2^{ - x}} = 5\)
Khi đó \(K = \dfrac{{5 + 5}}{{1 - \left( 5 \right)}} = \dfrac{{10}}{{ - 4}} = - \dfrac{5}{2}\)
Giá trị của \({\log _{{a^5}}}a\,\,\,(a > 0,\,\,a \ne 1)\) bằng:
Ta có: \({\log _{{a^5}}}a = \dfrac{1}{5}{\log _a}a = \dfrac{1}{5}.\)
Giá trị nhỏ nhất của hàm số \(y = {e^{{x^2}}}\) là:
Ta có: \({x^2} \ge 0 \Rightarrow {e^{{x^2}}} \ge {e^0} = 1\)
Số nghiệm của phương trình \({\log _5}(5x) - {\log _{25}}(5x) - 3 = 0\) là:
Điều kiện: \(5x > 0 \Rightarrow x > 0\)
Ta có: \({\log _5}(5x) - {\log _{25}}(5x) - 3 = 0 \)
\(\Leftrightarrow {\log _5}(5x) - {\log _{{5^2}}}(5x) - 3 = 0\)
\( \Leftrightarrow {\log _5}(5x) - \dfrac{1}{2}{\log _5}(5x) = 3\)
\( \Leftrightarrow \dfrac{1}{2}{\log _5}(5x) = 3 \)
\(\Leftrightarrow {\log _5}\left( {5x} \right) = 6\)
\( \Leftrightarrow 5x = {5^6} \Leftrightarrow x = {5^5}\).
Vậy phương trình đã cho có 1 nghiệm
Phương trình \({\log _2}x + {\log _2}(x - 1) = 1\) có tập nghiệm là:
Điều kiện: \(x > 1.\)
Ta có: \({\log _2}x + {\log _2}(x - 1) = 1\)
\(\Leftrightarrow \log {}_2\left[ {x\left( {x - 1} \right)} \right] = 1\)
\(\Leftrightarrow {x^2} - x = 2\)
\( \Leftrightarrow {x^2} - x - 2 = 0 \)
\(\Leftrightarrow \left( {x + 1} \right)\left( {x - 2} \right) = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}x = - 1(ktm)\\x = 2(tm)\end{array} \right.\)
Vậy phương trình đã cho có tập nghiệm là \(S = \left\{ { 2} \right\}\)
Cho hàm số \(y = {1 \over 2}{\tan ^2}x + \ln (\cos x)\). Đạo hàm y’ bằng:
Ta có: \(y = \dfrac{1}{2}{\tan ^2}x + \ln (\cos x)\)
\(\Rightarrow y' = {\left( {\dfrac{1}{2}{{\tan }^2}x + \ln (\cos x)} \right)^\prime }\)
\(= \tan x.\dfrac{1}{{\cos {x^2}}} - \dfrac{{\sin x}}{{\cos x}}\)
\(= \left( {{{\tan }^2}x + 1} \right)\tan x - \tan x = {\tan ^3}x.\)
Cho hàm số \(y = (x + 1).{e^x}\). Tính S= y’ – y
Ta có: \(y = (x + 1).{e^x} \)
\(\Rightarrow y' = {\left( {(x + 1).{e^x}} \right)^\prime } \)\(\,= {\left( {x + 1} \right)^\prime }.{e^x} + \left( {x + 1} \right){\left( {{e^x}} \right)^\prime } \)\(\,= {e^x} + \left( {x + 1} \right){e^x}\)
\( \Rightarrow y' - y = {e^x}\)
Số cạnh của một khối chóp tam giác là bao nhiêu?
Tứ diện có 6 cạnh.
Khi tăng kích thước mỗi cạnh của khối hộp chữ nhật lên 5 lần thì thể tích khối hộp chữ nhật tăng bao nhiêu lần?
\(\begin{array}{l}V = B.h = abh\\V' = B'.h' = 5a.5b.5h = 125abh = 125V\end{array}\)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA vuông góc với (ABC). Tính khoảng cách từ trọng tâm G của tam giác SAB đến (SAC)?
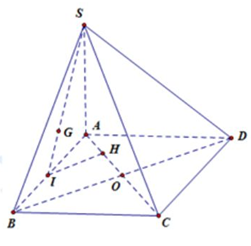
Gọi I là trung điểm của AB khi đó dựng \(IH \bot \left( {SAC} \right)\)
Khi đó \(IH = \dfrac{{OB}}{2} = \dfrac{{BD}}{4} = \dfrac{{a\sqrt 2 }}{4}\)
\(d\left( {G,\left( {SAC} \right)} \right) = \dfrac{2}{3}d\left( {I,\left( {SAC} \right)} \right)\)\(\, = \dfrac{2}{3}IH = \dfrac{{a\sqrt 2 }}{6}\)
Chọn B
Một chiếc xe ô tô có thùng đựng hàng hình hộp chữ nhật với kích thước 3 chiều lần lượt là 2m; 1,5m; 0,7m. Tính thể tích thùng đựng hàng của xe ôtô đó.
Thể tích của thùng hàng đó là:
\(V = abc = 2.1,5.0,7 = 2,1\left( {{m^3}} \right)\)
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng a. Gọi M là trung điểm của \(AA_1\). Thể tích khối chóp \(M.BC{A_1}\) là:
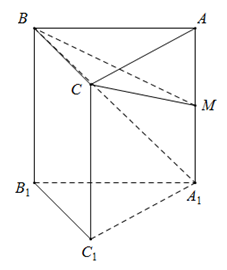
\(\Delta ABC\)là tam giác đều cạnh \(a\)nên có diện tích \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Ta có \(AM = \dfrac{{A{A_1}}}{2} = \dfrac{a}{2}\)
Hai tứ diện \(MABC\)và \(M{A_1}BC\)có chung đỉnh\(C\), diện tích hai đáy \(MAB\)và \(M{A_1}B\)bằng nhau nên có thể tích bằng nhau, suy ra
\({V_{M.BC{A_1}}} = {V_{M.ABC}} = \dfrac{1}{3}AM.{S_{ABC}} \)\(\,= \dfrac{{{a^3}\sqrt 3 }}{{24}}\)
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh \(SA = SB = SC = \dfrac{{a\sqrt 6 }}{3}\). Tính thể tích V của khối chóp đã cho.
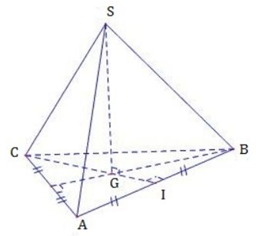
Gọi G là trọng tâm tam giác ABC, I là trung điểm của AB
\(\begin{array}{l}\left. \begin{array}{l}GA = GB = GC\\SA = SB = SC\end{array} \right\} \Rightarrow SG \bot \left( {ABC} \right)\\CG = \dfrac{2}{3}CI = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\\SG = \sqrt {S{C^2} - C{G^2}} \\ = \sqrt {{{\left( {\dfrac{{a\sqrt 6 }}{3}} \right)}^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{a\sqrt 3 }}{3}\\V = \dfrac{1}{3}SG.{S_{ABC}} \\\;\;\;\;= \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}}}{{12}}\end{array}\)
Công thức tính thể tích của khối lăng trụ có diện tích đáy B và chiều cao h
Công thức tính thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là: \(V = Bh.\)
Trung điểm các cạnh của một tứ diện đều là
Trung điểm các cạnh của một tứ diện đều là các đỉnh của một hình bát diện đều.
Khối lập phương là khối đa diện đều loại nào?
Khối lập phương là khối đa diện đều loại {4,3}

