Đường thẳng đi qua P(4;2) nên ta có \(4.a + b = 2\)
Đường thẳng đi qua Q(1;1) nên ta có \(4.a + b = 2\)

Ta có hệ phương trình 

\(\left\{ \begin{array}{l} 4.a + b = 2\\ 1.a + b = 1 \end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {a = \frac{1}{3}}\\ {b = \frac{2}{3}} \end{array}} \right.\)

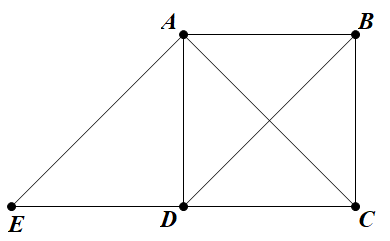
Gọi E là điểm đối xứng của C qua D. Khi đó ABDE là hình bình hành nên \(\overrightarrow {BD} = \overrightarrow {AE} \)

Khi đó

\(|\overrightarrow {AC} + \overrightarrow {BD} | = |\overrightarrow {AC} + \overrightarrow {AE} | = |2\overrightarrow {AD} | = 2.|\overrightarrow {AD} | = 2a\)

Phương trình hoành độ giao điểm là nghiệm của phương trình

\(\begin{array}{l} 2{x^2} + 6x + 3 = {\rm{ - 2 x - 3}}\\ \Leftrightarrow 2{x^2} + 8x + 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = - 3 \Rightarrow y = 3\\ x = - 1 \Rightarrow y = - 1 \end{array} \right. \end{array}\)

Vậy tung độ giao điểm là y=-1 và y=3

Parabol đi qua điểm M(3;0) nên ta có: 

\(\begin{array}{l} 0 = a{.3^2} - 4.3 + c\\ \Leftrightarrow 9a - 12 + c = 0\,\,\,(1) \end{array}\)

Parabol có trục đối xứng x=2 nên ta có: 

\(\begin{array}{l} \frac{{ - b}}{{2a}} = 2\\ \Leftrightarrow \frac{4}{{2a}} = 2\\ \Leftrightarrow a = 1 (2) \end{array}\)

Từ (1) và (2) ta có hệ

\(\left\{ \begin{array}{l} 9a - 12 + c = 0\\ a = 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 1\\ c = 3 \end{array} \right.\)

Gọi M là trung điểm BC. khi đó AM là trung tuyến trong tam giác đều ABC nên  \(AM=\frac{a \sqrt{3}}{2}\)

Ta có 

\(|\overrightarrow {AB} - \overrightarrow {CA} | = |\overrightarrow {AB} + \overrightarrow {AC} | = |2\overrightarrow {AM} | = 2.|\overrightarrow {AM} | = 2.\frac{{a\sqrt 3 }}{2} = a\sqrt 3 \)

Ta có \(\overrightarrow {AC} = (m - 1; - 5);\overrightarrow {AB} = (1;1)\)

Để A, B, C thẳng hàng thì \(\overrightarrow {AB}\,\,và\,\,\overrightarrow {AC}\) cùng phương

\(\Leftrightarrow \frac{{m - 1}}{1} = \frac{{ - 5}}{1} \Leftrightarrow m = - 4\)

Ta có
\(\begin{array}{l} \overrightarrow {AB} = (1;4);\overrightarrow {AC} = (m + 3;n - 1)\\ 2\overrightarrow {AB} - 3\overrightarrow {AC} = \overrightarrow 0 \\ \Leftrightarrow 2\left( {1;4} \right) - 3\left( {m + 3;n - 1} \right) = \overrightarrow 0 \\ \Leftrightarrow \left\{ \begin{array}{l} - 3m - 7 = 0\\ - 3n + 11 = 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m = \frac{{ - 7}}{3}\\ n = \frac{{11}}{3} \end{array} \right.\\ \Rightarrow 3m + 3n - 4 = 0 \end{array}\)

ĐK: \(\begin{array}{l} \left\{ \begin{array}{l} x - 1 \ne 0\\ x + 3 \ge 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x \ne 1\\ x \ge 3 \end{array} \right. \end{array}\)

Vây ^{\(D=[-3 ; 1) \cup(1 ;+\infty)\)}

Parabol (P) đi qua điểm A(-1;0) nên \(a{\left( { - 1} \right)^2} + b\left( { - 1} \right) + c = 0 \Leftrightarrow a - b + c = 0\)

Parabol (P) đi qua điểm B(0;-4) nên \(a{\left( 0 \right)^2} + b\left( 0 \right) + c = - 4 \Leftrightarrow c = - 4\)

Parabol (P) đi qua điểm C(1;-6) nên \(a{\left( 1 \right)^2} + b\left( 1 \right) + c = 6 \Leftrightarrow a + b + c =- 6\)

Ta có hệ phương trình:

\(\begin{array}{l} \left\{ \begin{array}{l} a - b + c = 0\\ c = - 4\\ a + b + c = -6 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 1\\ b = -3\\ c = - 4 \end{array} \right. \end{array}\)

Vậy (P) có phương trình là: \(y=x^{2}-3 x-4\)

Ta có 

\(\begin{array}{l} A \cup B = \left( {0;4} \right)\\ {C_\mathbb{R}}(A \cup B) = \left( { - \infty ;0} \right] \cup \left[ {4; + \infty } \right) \end{array}\)

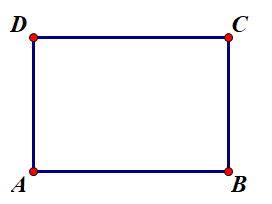
Chọn D vì 

\(\overrightarrow{A D}\,\,và\,\,\overrightarrow{B C}\) cùng hướng

\(|\overrightarrow{A D}|=|\overrightarrow{B C}|\)

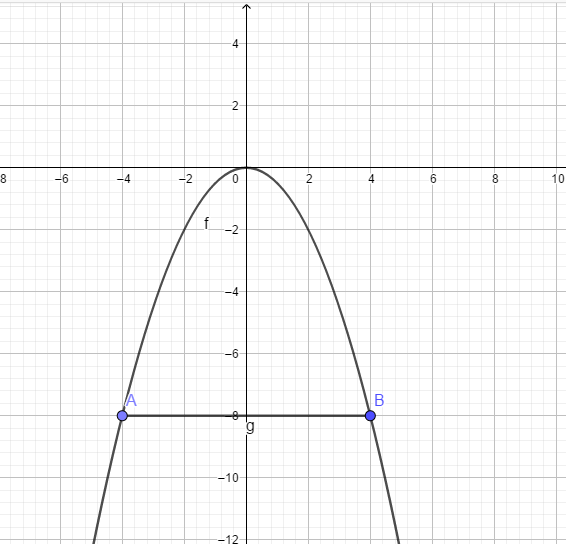
Cổng có chiều rộng bằng 8 nên AB=2x=8 hay x=4

khi đó \(y=\frac{-1}{2} x^{2}=\frac{-1}{2} .16=-8\)

Vậy chiều cao của cổng là 8m

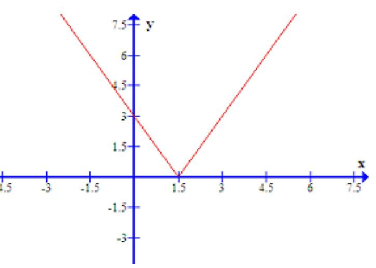
Đồ thị hàm số nằm trên Ox nên \(y\ge 0\). Loại A

Đồ thị hàm số bậc nhất là đường thẳng nên loại C và D.

Vậy chọn B

Theo định nghĩa mệnh đề phủ định

ta có phủ định của mệnh đề là \(\exists x \in \mathbb{R}, x^{2}+x+1 \leq 0\)

A sai vì \(0\notin(0;5)\)

C sai vì \((-\infty ; 2) \cup(2 ;+\infty)=(-\infty ;+\infty)\backslash \{2\}\)

D sai vì \((1 ; 2) \cup(2 ; 5)=(1 ; 5)\backslash \{2\}\)

3 đường thẳng đồng quy khi chúng cắt nhau tại 1 điểm A. 

3 đường thẳng cắt nhau khi \(m\ne -5 \,\,và\,\,m\ne 3\)

Gọi A là giao điểm của đường thẳng y=-5(x+1) và y=mx+3. Khi đó ta có phương trình hoành độ giao điểm

\(\begin{array}{l} - 5\left( {x + 1} \right) = mx + 3\\ \Leftrightarrow - 5x - 5 - mx - 3 = 0\\ \Leftrightarrow \left( { - 5 - m} \right)x = 8\\ \Leftrightarrow x = \frac{8}{{ - 5 - m}} \end{array}\)

\(\Rightarrow y = - 5\left( {x + 1} \right) = - 5.\left( {\frac{8}{{ - 5 - m}} + 1} \right) = - 5.\frac{{3 - m}}{{ - 5 - m}} = \frac{{15 - 5m}}{{5 + m}}\)

Vậy \(A\left( {\frac{8}{{ - 5 - m}};\frac{{15 - 5m}}{{5 + m}}} \right)\)

3 đường thẳng đồng quy khi A cũng nằm trên đường thẳng y=3x+m. Khi đó

\(\begin{array}{l} \frac{{15 - 5m}}{{5 + m}} = 3.\frac{8}{{ - 5 - m}} + m\\ \Leftrightarrow \left\{ \begin{array}{l} m \ne - 5\\ \left[ \begin{array}{l} m = - 13\\ m = 3 (loại) \end{array} \right. \end{array} \right. \end{array}\)

Vây m=-13

Hàm số xác định trên R khi và chỉ khi

\({x^2} - 3x + 2 - m \ne0\)

hay \({x^2} - 3x + 2 - m =0(*)\) vô nghiệm

Ta có

\(\Delta = 9 - 4\left( {2 - m} \right) = 1 + 4m\)

(*) vô nghiệm khi \(\Delta < 0 \Leftrightarrow 1 + 4m < 0 \Leftrightarrow m <- \frac{1}{4}\)

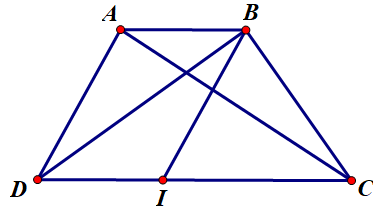
gọi I là trung điểm CD. Khi đó ADIB là hình bình hành

và AB=DI=IC=3a

Ta có

\(|\overrightarrow {AB} + \overrightarrow {CD} | = |\overrightarrow {DI} + \overrightarrow {CD} | = |\overrightarrow {DI} - \overrightarrow {DC} | = |\overrightarrow {CI} | = 3a\)

hoành độ đỉnh của (P) là \(x_I = \frac{{ - b}}{{2a}} = \frac{2}{6} = \frac{1}{3}\)

Khi đó \({y_I} = 3.{\left( {\frac{1}{3}} \right)^2} - 2.\frac{1}{3} + 1 = \frac{2}{3}\)

Dựa vào đồ thi hàm số ta thấy:

Đồ thị hàm số có hoành độ đỉnh là x=1

Đồ thị hàm số đi qua M(3;4) và N(0;2)

Ta có \(x = 1 \Leftrightarrow \frac{{ - b}}{{2a}} = 1 \Leftrightarrow - b = 2a\,\,(1)\)

Đồ thị hàm số đi qua M(3;4) nên ta có 

\(a{.3^2} + b.3 + c = 4 \Leftrightarrow 9a + 3b + c = 4\,\,(2)\)

Đồ thị hàm số đi qua  N(0;2) nên

\(a{.0} + b.0 + c = 2 \Leftrightarrow c = 2\,\,(3)\)

(1), (2), (3) ta có hệ

\(\left\{ \begin{array}{l} - b = 2a\\ 9a + 3b + c = 4\\ c = 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = \frac{2}{3}\\ b = - \frac{4}{3}\\ c = 2 \end{array} \right.\)

Vậy (P): \(y=\frac{2}{3} x^{2}-\frac{4}{3} x+2\)

Dựa vào định nghĩa hiệuc ủa hai tập hợp ta có \(B=\mathbb{R} \backslash(0 ;+\infty)=(-\infty ; 0]\)

Ta có

\(\begin{array}{l} \overrightarrow {AB} = \left( { - 2;2} \right) \Rightarrow AB = \sqrt {{{\left( { - 2} \right)}^2} + {2^2}} = 2\sqrt 2 \\ \overrightarrow {AC} = \left( { - 3; - 1} \right) \Rightarrow AC = \sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10} \\ \overrightarrow {BC} = \left( { - 1; - 3} \right) \Rightarrow BC = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2}} = \sqrt {10} \end{array}\)

Ta thấy AC=BC nên tam giác ABC cân tại C.

Chọn A vì xét hàm số 

TXD: \(D=\mathbb{R}\)

\(\forall x\in D \Rightarrow -x\in D\)

\(\begin{array}{l} f( - x) = \left| {2.\left( { - x} \right) + 2016} \right| + \left| {2.\left( { - x} \right) - 2016} \right|\\ = \left| { - 2x + 2016} \right| + \left| { - 2x - 2016} \right|\\ = \left| { - \left( {2x - 2016} \right)} \right| + \left| { - \left( {2x + 2016} \right)} \right|\\ = \left| {2x - 2016} \right| + \left| {2x + 2016} \right| = f(x) \end{array}\)

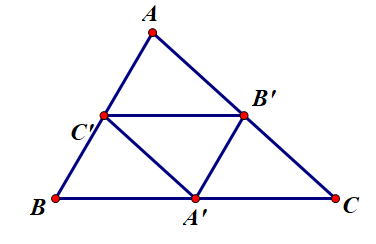
Chọn B vì:

B' là trung điểm AC, A' là trùg điểm BC nên A'B' là đường trung bình cảu tam giác ABC nên A'B'//AB

Khi đó \(\overrightarrow{A^{\prime} B^{\prime}}\) cừng hướng với \(\overrightarrow{BA}\)

Tập A có 4 phần tử nên số tập con của A là \(2^4=16\)

Theo lý thuyết:

Nếu O là trung điểm của AB thì \(\overrightarrow{O A}+\overrightarrow{O B}=\overrightarrow{0}\)

Nếu \(\overrightarrow{O A}+\overrightarrow{O B}=\overrightarrow{0}\Leftrightarrow \overrightarrow{AO}=\overrightarrow{O B}\), khi đó OA=OB và O, A, B thẳng hàng nên O là trung điểm của AB

\(\frac{{ - b}}{{2a}} = 1\)

Hàm số bậc hai có a=1>0 nên hàm số đồng biến trên \(\left(1 ;+\infty\right)\) và nghịch biến trên \(\left(-\infty ; 1\right)\)

Vậy chọn hàm số đồng biến trên \(\left(-\infty ; \frac{-b}{2 a}\right)\)

Hàm số bậc nhất đồng biến trên \(\mathbb{R}\) khih và chỉ khi \(a=m-2>0\Leftrightarrow m>2\)

Đặt C(x;y)

\(\begin{array}{l} \overrightarrow {AB} = \left( { - 1;1} \right)\\ \overrightarrow {OC} = \left( {x;y} \right) \end{array}\)

OABC là hình bình hành khi và chỉ khi

\(\begin{array}{l} \overrightarrow {AB} = \overrightarrow {OC} \\ \Leftrightarrow \left\{ \begin{array}{l} x = - 1\\ y = 1 \end{array} \right. \end{array}\)

B nằm giữa A và C nên ta có 

\(\left| {\overrightarrow {AC} } \right| = AC = \left| {\overrightarrow {AB} } \right| + \left| {\overrightarrow {BC} } \right| = 2a + 5a = 7a\)

\(A \cap B\) là tập hợp tất cả những phần tử thuộc A và B nên ta có:

Vậy 

\((-1 ; 0) \cup(4 ; 5)\)

\(A \cap B\) là tập hợp tất cả những phần tử thuộc A và B nên ta có:

Vậy 

\((-1 ; 0) \cup(4 ; 5)\)

Đặt \(t=|x|(t>0)\)

Phương trình trở thành: \(t^{2}-2t+1-m=0 (*)\) 

Phương trình có 4 nghiệm phân biệt khi (*) có hai nghiệm phân biệt dương.

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} \Delta = 4 - 4\left( {1 - m} \right) > 0\\ S = \frac{{ - b}}{a} > 0\\ P = \frac{c}{a} > 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} 4m > 0\\ 2 > 0(lld)\\ 1 - m > 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m > 0\\ m < 1 \end{array} \right. \Leftrightarrow 0 < m < 1 \end{array}\)

+ Với x> 0 ta xét hàm sô \(f(x)=\frac{x}{x+1}\). Hàm số luôn xác định với mọi x>0

+ Với \(-1 \leq x \leq 0\) xét hàm số \(f(x)=\frac{\sqrt[3]{x+1}}{x-1}\). Hàm số luôn xác định với mọi \(x\in [-1;0]\)

Vâyu tập xác định của hàm số là  \([-1 ;+\infty)\)

Ta có: \(2\vec a-3\vec b=2(2;1)-3(-1;3)=(7;-7)\)

Nếu \(\vec{c}=(m ; n)\)  cùng phương với \(2 \vec{a}-3 \vec{b}\)  khi

\(\frac{7}{m} = \frac{{ - 7}}{n} \Leftrightarrow 7n = - 7m \Leftrightarrow 7n + 7m = 0 \Leftrightarrow m + n = 0\)

Đường thẳng cần tìm có phương trình: y=ax+b.

+Đường thẳng cần tìm song song với đường thẳng y=3x-2 nên a=3

Vậy phương trình đường thẳng có dạng: y=3x+b

+ Đường thẳng đi qua điểm M(2;3) nên ta có:

\(3.2+b=3\Leftrightarrow b=-3\)

Vậy phương trình đường thẳng cần tìm là: y=3x-3

ĐKXĐ:

\(\left\{ \begin{array}{l} x + 2 \ge 0\\ x - 3 \ne 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ x \ne 3 \end{array} \right.\)

Vậy \(D=[-2 ;+\infty) \backslash\{3\}\)

ĐKXĐ:

\(\left\{ \begin{array}{l} {x^2} - 2x + 4 \ge 0\\ |x| + 1 \ne 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {\left( {x - 1} \right)^2} + 3 \ge 0(llđ)\\ |x|\, \ne - 1(llđ) \end{array} \right.\)

Vậy \(D=\mathbb{R}\)

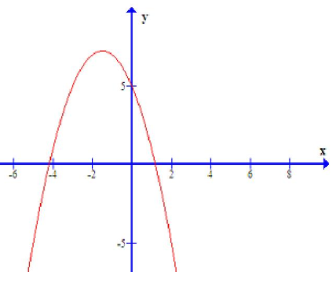
Đồ thị hàm số cắt trục tung tại y=5 nên \(c=5\Rightarrow c>0\)

Bề lõm của đồ thị hàm số hướng xuống nên a<0.

Đồ thị hàm số có trục đối xứng 

\(x = \frac{{ - b}}{{2a}} < 0\) mà a<0 nên b<0

Vậy \(\left\{\begin{array}{l}a<0 \\ b<0 \\ c>0\end{array}\right.\)

Ta có:

\(\begin{array}{l} \overrightarrow {IA} + 2\overrightarrow {IB} + 3\overrightarrow {IC} = \vec 0\\ \Leftrightarrow \overrightarrow {IA} + 2\left( {\overrightarrow {IA} + \overrightarrow {AB} } \right) + 3\left( {\overrightarrow {IA} + \overrightarrow {AC} } \right) = \overrightarrow 0 \\ \Leftrightarrow IA + 2\overrightarrow {IA} + 2\overrightarrow {AB} + 3\overrightarrow {IA} + 3\overrightarrow {AC} = \overrightarrow 0 \\ \Leftrightarrow 6\overrightarrow {IA} + 2\overrightarrow {AB} + 3\overrightarrow {AC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} + \overrightarrow {\frac{1}{2}\overrightarrow {AC} } \end{array}\)

Theo kháo niệm giao của hai tập hợp thì 

\(A=(-5 ; 3) \cap(0 ; 7)=(0;3)\)

Đường thẳng y=ax+b đi quan điểm A(1;0-) nên ta có: a+b=0 (1)

Đường thẳng y=ax+b đi quan điểm B(3;0) nên ta có: b=3 (2)

Từ (1) và (2) ta có \(\left\{\begin{array}{l}a=-3 \\ b=3\end{array}\right.\)

Chọn C vì:

\(\begin{aligned} &2 \overrightarrow{I A}+\overrightarrow{I B}+\overrightarrow{I C}\\ &=2 \cdot \overrightarrow{I A}+2 \overrightarrow{I M}\\ &=2(\overrightarrow{I A}+\overrightarrow{IM})=2 \cdot \overrightarrow{0}=\overrightarrow{0} \end{aligned}\)

Với x=-2 ta có

\(y = \left( {m - 1} \right)\left( { - 2} \right) + 2m + 1\; = - 2m + 2 + 2m + 1 = 3\)

Vậy đường thẳng luôn đi qua (-2;3) với mọi giá trị m.

ĐKXĐ: \(x-1\ne 0\Leftrightarrow x\ne 1\)

Vậy \(D=\mathbb{R} \backslash\{1\}\)

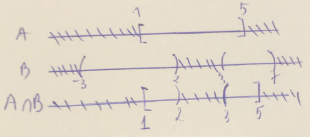
Vậy \(A\cup B=[1 ; 2) \cup(3 ; 5]\)

GỌi A, B, C lần lượt là tập hợp những ngày mua, ngày có gió và ngày lạnh.

Ta có

\(\begin{array}{l} (A \cup B \cup C)=n A+n B+n C-n(A \cap B)-n(B \cap C)-n(A \cap C)+n( A \cap B \cap C)\\ =10+8+6-5-4-3+1=13 \end{array}\)

\(\left\{ \begin{array}{l} {x_C} = 3{x_G} - {x_A} - {x_B}\\ {y_C} = 3{y_G} - {y_A} - {y_B} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {x_C} = 3.0 + 1 - 2 = - 1\\ {y_C} = 3.7 - 4 - 5 = 12 \end{array} \right.\)

Vậy C(-1 ; 12)

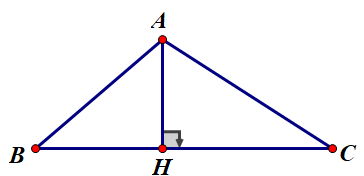
Ta có tam giác ABC đều, AH là đường cao nên AH cũng là đường trung tuyến. Khi đó

\(AH = \frac{{\sqrt 3 }}{2}BC \text{ hay } \left| {\overrightarrow {AH} } \right| = \frac{{\sqrt 3 }}{2}\left| {\overrightarrow {BC} } \right|\)

Theo định nghĩa hai vec tơ bằng nhau ta có 

Hai vectơ được gọi là bằng nhau khi và chỉ khi chúng cùng hướng và độ dài của chúng bằng nhau.