+Tìm tọa độ giao điểm A của đường thẳng \(y=2 x-1\,\,và\,\, y=x+2\)

Phương trình hoành độ giao điểm của đồ thị hai hàm số là:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabbkdaYiabbccaGiabbIha4jabb2caTiab % bgdaXiabb2da9iabbIha4jabbUcaRiabbkdaYaqaaiabgsDiBlabdI % ha4jabg2da9iabiodaZaqaaiabgkDiElabdMha5jabg2da9iabioda % ZiabgUcaRiabikdaYiabg2da9iabiwda1aaaaa!53AA! \begin{array}{l} {\rm{2 x - 1 = x + 2}}\\ \Leftrightarrow x = 3\\ \Rightarrow y = 3 + 2 = 5 \end{array}\)

Vậy A(3;5)

+ để ba đường thẳng đồng quy thì 3 đường thẳng phải cắt nhau tại 1 điểm\(\Leftrightarrow\)giao điểm A(3;5) thuộc đường thẳng \(y=(m-1) x+8\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabgsDiBpaabmaabaGaemyBa0MaeyOeI0Ia % eGymaedacaGLOaGaayzkaaGaeiOla4IaeG4mamJaey4kaSIaeGioaG % Jaeyypa0JaeGynaudabaGaeyi1HSTaeG4mamZaaeWaaeaacqWGTbqB % cqGHsislcqaIXaqmaiaawIcacaGLPaaacqGH9aqpcqGHsislcqaIZa % WmaeaacqGHuhY2cqWGTbqBcqGHsislcqaIXaqmcqGH9aqpcqGHsisl % cqaIXaqmaeaacqGHuhY2cqWGTbqBcqGH9aqpcqaIWaamaaaa!6112! \begin{array}{l} \Leftrightarrow \left( {m - 1} \right).3 + 8 = 5\\ \Leftrightarrow 3\left( {m - 1} \right) = - 3\\ \Leftrightarrow m - 1 = - 1\\ \Leftrightarrow m = 0 \end{array}\)

vec tơ chỉ phương của đường thẳng là \(\overrightarrow {AB}=(-2;2)\)

Một vec tơ pháp tuyến của đường thẳng là \(\vec n=(2;2)\)

Phương trình đường thẳng đi qua hai điểm A, B là:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabikdaYmaabmaabaGaemiEaGNaeyOeI0Ia % eGymaedacaGLOaGaayzkaaGaey4kaSIaeGOmaiZaaeWaaeaacqWG5b % qEcqGHsislcqaIYaGmaiaawIcacaGLPaaacqGH9aqpcqaIWaamaeaa % cqGHuhY2cqaIYaGmcqWG4baEcqGHsislcqaIYaGmcqGHRaWkcqaIYa % GmcqWG5bqEcqGHsislcqaI0aancqGH9aqpcqaIWaamaeaacqGHuhY2 % cqaIYaGmcqWG4baEcqGHRaWkcqaIYaGmcqWG5bqEcqGHsislcqaI2a % GncqGH9aqpcqaIWaamaeaacqGHuhY2cqWG4baEcqGHRaWkcqWG5bqE % cqGHsislcqaIZaWmcqGH9aqpcqaIWaamaeaacqGHuhY2cqWG4baEcq % GHRaWkcqWG5bqEcqGH9aqpcqaIZaWmaaaa!7572! \begin{array}{l} 2\left( {x - 1} \right) + 2\left( {y - 2} \right) = 0\\ \Leftrightarrow 2x - 2 + 2y - 4 = 0\\ \Leftrightarrow 2x + 2y - 6 = 0\\ \Leftrightarrow x + y - 3 = 0\\ \Leftrightarrow x + y = 3 \end{array}\)

Hoành độ đỉnh của parabol:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabdIha4jabg2da9maalaaabaGaeyOeI0Ia % emOyaigabaGaeGOmaiJaemyyaegaaaqaaiabgsDiBlabdIha4jabg2 % da9maalaaabaGaeyOeI0YaaeWaaeaacqGHsislcqaIZaWmaiaawIca % caGLPaaaaeaacqaIYaGmcqGGUaGlcqaIYaGmaaaabaGaeyi1HSTaem % iEaGNaeyypa0ZaaSaaaeaacqaIZaWmaeaacqaI0aanaaaaaaa!54E9! \begin{array}{l} x = \frac{{ - b}}{{2a}}\\ \Leftrightarrow x = \frac{{ - \left( { - 3} \right)}}{{2.2}}\\ \Leftrightarrow x = \frac{3}{4} \end{array}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeGaemyEaKNaeyypa0JaeyOe % I0IaemiEaG3damaaCaaaleqabaWdbiabikdaYaaakiabgkHiTiabdI % ha4jabgUcaRiabigdaXiabiwda1aqaaiabg2da9iabgkHiTmaabmaa % baGaemiEaG3damaaCaaaleqabaWdbiabikdaYaaak8aacqGHRaWkpe % GaemiEaGNaeyOeI0IaeGymaeJaeGynaudacaGLOaGaayzkaaaabaGa % eyypa0JaeyOeI0YaaeWaaeaacqWG4baEdaahaaWcbeqaaiabikdaYa % aakiabgUcaRiabikdaYiabc6caUiabdIha4jabc6caUmaalaaabaGa % eGymaedabaGaeGOmaidaaiabgUcaRmaalaaabaGaeGymaedabaGaeG % inaqdaaiabgkHiTmaalaaabaGaeGymaedabaGaeGinaqdaaiabgkHi % TiabigdaXiabiwda1aGaayjkaiaawMcaaaqaaiabg2da9iabgkHiTm % aadmaabaWaaeWaaeaacqWG4baEcqGHRaWkdaWcaaqaaiabigdaXaqa % aiabikdaYaaaaiaawIcacaGLPaaadaahaaWcbeqaaiabikdaYaaaki % abgkHiTmaalaaabaGaeGOnayJaeGymaedabaGaeGinaqdaaaGaay5w % aiaaw2faaaqaaiabg2da9iabgkHiTmaabmaabaGaemiEaGNaey4kaS % YaaSaaaeaacqaIXaqmaeaacqaIYaGmaaaacaGLOaGaayzkaaWaaWba % aSqabeaacqaIYaGmaaGccqGHRaWkdaWcaaqaaiabiAda2iabigdaXa % qaaiabisda0aaaaaaa!834B! \begin{array}{l} y = - {x^2} - x + 15\\ = - \left( {{x^2} + x - 15} \right)\\ = - \left( {{x^2} + 2.x.\frac{1}{2} + \frac{1}{4} - \frac{1}{4} - 15} \right)\\ = - \left[ {{{\left( {x + \frac{1}{2}} \right)}^2} - \frac{{61}}{4}} \right]\\ = - {\left( {x + \frac{1}{2}} \right)^2} + \frac{{61}}{4} \end{array}\)

Ta có

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % Waaqaafaaakqaabeaeaaaaaaaaa8qabaGaeyOeI0YaaeWaaeaacqWG % 4baEcqGHRaWkdaWcaaqaaiabigdaXaqaaiabikdaYaaaaiaawIcaca % GLPaaadaahaaWcbeqaaiabikdaYaaakiabgsMiJkabicdaWaqaaiab % gkDiElabgkHiTmaabmaabaGaemiEaGNaey4kaSYaaSaaaeaacqaIXa % qmaeaacqaIYaGmaaaacaGLOaGaayzkaaWaaWbaaSqabeaacqaIYaGm % aaGccqGHRaWkdaWcaaqaaiabiAda2iabigdaXaqaaiabisda0aaacq % GHKjYOdaWcaaqaaiabiAda2iabigdaXaqaaiabisda0aaaaaaa!5872! \begin{array}{l} - {\left( {x + \frac{1}{2}} \right)^2} \le 0\\ \Rightarrow - {\left( {x + \frac{1}{2}} \right)^2} + \frac{{61}}{4} \le \frac{{61}}{4} \end{array}\)

Vậy giá trị lớn nhất của hàm số là \(\max y=\frac{61}{4}\)

Phương trình hoành độ giao điểm

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabdIha4naaCaaaleqabaGaeGOmaidaaOGa % eyOeI0IaemiEaGNaeyypa0JaemyBa0MaemiEaGNaeyOeI0IaeGymae % dabaGaeyi1HSTaemiEaG3aaWbaaSqabeaacqaIYaGmaaGccqGHsisl % cqWG4baEcqGHsislcqWGTbqBcqWG4baEcqGHRaWkcqaIXaqmcqGH9a % qpcqaIWaamaeaacqGHuhY2cqWG4baEdaahaaWcbeqaaiabikdaYaaa % kiabgkHiTmaabmaabaGaeGymaeJaey4kaSIaemyBa0gacaGLOaGaay % zkaaGaemiEaGNaey4kaSIaeGymaeJaeyypa0JaeGimaadabaGaeyiL % dqKaeyypa0ZaaeWaaeaacqaIXaqmcqGHRaWkcqWGTbqBaiaawIcaca % GLPaaadaahaaWcbeqaaiabikdaYaaakiabgkHiTiabisda0iabc6ca % UiabigdaXiabc6caUiabigdaXiabg2da9iabigdaXiabgUcaRiabik % daYiabd2gaTjabgUcaRiabd2gaTnaaCaaaleqabaGaeGOmaidaaOGa % eyOeI0IaeGinaqdabaGaeyypa0JaemyBa02aaWbaaSqabeaacqaIYa % GmaaGccqGHRaWkcqaIYaGmcqWGTbqBcqGHsislcqaIZaWmaaaa!85AF! \begin{array}{l} {x^2} - x = x - m\ \Leftrightarrow {x^2} - x - x + m = 0\\ \Leftrightarrow {x^2} - 2x + m = 0(*)\\ \Delta = {\left( {-2} \right)^2} - 4.1.m =4-4m \end{array}\)

Để (P) cắt (d) tại hai điểm phân biệt thì (*) có hai nghiệm phân biệt

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % Waaqaafaaakqaabeqaaiabgs5aejabg2da9iabisda0iabgkHiTiab % isda0iabd2gaTjabg6da+iabicdaWaqaaiabgsDiBlabd2gaTjabgY % da8iabigdaXaaaaa!4955! \begin{array}{l} \Delta = 4 - 4m > 0\\ \Leftrightarrow m < 1 \end{array}\)

Vậy \(m \in(-\infty,1)\)

ĐKXĐ: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaadaGabaabaeqabaGaeGOmaiJaemiEaGNaeyOeI0Ia % eGymaeJaeyyzImRaeGimaadabaGaemiEaGNaey4kaSIaeG4mamJaey % yzImRaeGimaadaaiaawUhaaiabgsDiBpaaceaaeaqabeaacqWG4baE % cqGHLjYSdaWcaaqaaiabigdaXaqaaiabikdaYaaaaeaacqWG4baEcq % GHLjYScqGHsislcqaIZaWmaaGaay5EaaGaeyO0H4TaemiEaGNaeyyz % Im7aaSaaaeaacqaIXaqmaeaacqaIYaGmaaaaaa!5E78! \left\{ \begin{array}{l} 2x - 1 \ge 0\\ x + 3 \ge 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge \frac{1}{2}\\ x \ge - 3 \end{array} \right. \Rightarrow x \ge \frac{1}{2}\)

Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaacqWGebarcqGH9aqpdaqcsaqaamaalaaabaGaeGym % aedabaGaeGOmaidaaiabcUda7iabgUcaRiabg6HiLcGaay5waiaawM % caaaaa!4429! D = \left[ {\frac{1}{2}; + \infty } \right)\) hay \(D=\mathbb{R} \backslash\left(-\infty, \frac{1}{2}\right)\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeGaeGOmaiJaemiEaG3damaa % CaaaleqabaWdbiabikdaYaaakiabgkHiTiabdIha4jabgUcaRiabio % daZiabg2da9iabikdaYiabd2gaTjabgkHiTiabigdaXaqaaiabgsDi % BlabikdaYiabdIha49aadaahaaWcbeqaa8qacqaIYaGmaaGccqGHsi % slcqWG4baEcqGHRaWkcqaIZaWmcqGHsislcqaIYaGmcqWGTbqBcqGH % RaWkcqaIXaqmcqGH9aqpcqaIWaamaeaacqGHuhY2cqaIYaGmcqWG4b % aEpaWaaWbaaSqabeaapeGaeGOmaidaaOGaeyOeI0IaemiEaGNaey4k % aSIaeGinaqJaeyOeI0IaeGOmaiJaemyBa0Maeyypa0JaeGimaadaaa % a!6921! \begin{array}{l} 2{x^2} - x + 3 = 2m - 1\,\,\,\,(1)\\ \Leftrightarrow 2{x^2} - x + 3 - 2m + 1 = 0\\ \Leftrightarrow 2{x^2} - x + 4 - 2m = 0\,\,\,\,\,(2) \end{array}\)

Ta có 

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % Waaqaafaaakqaabeaeaaaaaaaaa8qabaGaeyiLdqKaeyypa0JaemOy % ai2aaWbaaSqabeaacqaIYaGmaaGccqGHsislcqaI0aancqWGHbqycq % WGJbWyaeaacqGH9aqpdaqadaqaaiabgkHiTiabigdaXaGaayjkaiaa % wMcaamaaCaaaleqabaGaeGOmaidaaOGaeyOeI0IaeGinaqJaeiOla4 % IaeGOmaiJaeiOla4YaaeWaaeaacqaI0aancqGHsislcqaIYaGmcqWG % TbqBaiaawIcacaGLPaaaaeaacqGH9aqpcqaIXaqmcqGHsislcqaIZa % WmcqaIYaGmcqGHRaWkcqaIXaqmcqaI2aGncqWGTbqBaeaacqGH9aqp % cqaIXaqmcqaI2aGncqWGTbqBcqGHsislcqaIZaWmcqaIXaqmaaaa!6494! \begin{array}{l} \Delta = {b^2} - 4ac\\ = {\left( { - 1} \right)^2} - 4.2.\left( {4 - 2m} \right)\\ = 1 - 32 + 16m\\ = 16m - 31 \end{array}\)

Phương trình (1) vô nghiệm \(\Leftrightarrow\) (2) vô nghiệm

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakabaaaaaaaaapeqaaiabgsDiBlabgs5aejabgYda8iab % icdaWiabgsDiBlabigdaXiabiAda2iabd2gaTjabgkHiTiabiodaZi % abigdaXiabgYda8iabicdaWiabgsDiBlabd2gaTjabgYda8maalaaa % baGaeG4mamJaeGymaedabaGaeGymaeJaeGOnaydaaaaa!53DE! \Leftrightarrow \Delta < 0 \Leftrightarrow 16m - 31 < 0 \Leftrightarrow m < \frac{{31}}{{16}}\)

ĐKXĐ:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabgkHiTiabisda0iabdIha4jabgUcaRiab % iodaZiabg6da+iabicdaWaqaaiabgsDiBlabgkHiTiabisda0iabdI % ha4jabg6da+iabgkHiTiabiodaZaqaaiabgsDiBlabdIha4jabgYda % 8maalaaabaGaeyOeI0IaeG4mamdabaGaeyOeI0IaeGinaqdaaaqaai % abgsDiBlabdIha4jabgYda8maalaaabaGaeG4mamdabaGaeGinaqda % aaaaaa!5A4E! \begin{array}{l} - 4x + 3 > 0\\ \Leftrightarrow - 4x > - 3\\ \Leftrightarrow x < \frac{{ - 3}}{{ - 4}}\\ \Leftrightarrow x < \frac{3}{4} \end{array}\)

Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaacqWGebarcqGH9aqpdaqadaqaaiabgkHiTiabg6Hi % LkabcUda7maalaaabaGaeG4mamdabaGaeGinaqdaaaGaayjkaiaawM % caaaaa!43F2! D = \left( { - \infty ;\frac{3}{4}} \right)\) hay \(D=\mathbb{R} \backslash\left[\frac{3}{4},+\infty\right)\)

Gọi (d) là đường thẳng cần tìm

Ta có 

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabbkdaYiabbccaGiabbIha4jabb2caTiab % bodaZiabbccaGiabbMha5jabb2da9iabbwda1aqaaiabgsDiBlabbo % daZiabbMha5jabb2da9iabbkdaYiabbIha4jabb2caTiabbwda1aqa % aiabgsDiBlabbMha5jabb2da9maalaaabaGaeGOmaiJaemiEaGNaey % OeI0IaeGynaudabaGaeG4mamdaaaqaaiabgsDiBlabdMha5jabg2da % 9maalaaabaGaeGOmaidabaGaeG4mamdaaiabdIha4jabgkHiTmaala % aabaGaeGynaudabaGaeG4mamdaaaaaaa!6384! \begin{array}{l} {\rm{2 x - 3 y = 5}}\\ \Leftrightarrow {\rm{3y = 2x - 5}}\\ \Leftrightarrow {\rm{y = }}\frac{{2x - 5}}{3}\\ \Leftrightarrow y = \frac{2}{3}x - \frac{5}{3} \end{array}\)

(d) song song với đường thẳng \(y=\frac{2}{3} x-\frac{5}{3}\) nên phương tình đường thẳng (d): \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaacqWG5bqEcqGH9aqpdaWcaaqaaiabikdaYaqaaiab % iodaZaaacqWG4baEcqGHRaWkcqWGIbGyaaa!431B! y = \frac{2}{3}x + b\)

Lại có:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabdMeajnaabmaabaGaeG4mamJaei4oaSJa % eyOeI0IaeGymaedacaGLOaGaayzkaaGaeyicI4SaemizaqMaeyO0H4 % 9aaSaaaeaacqaIYaGmaeaacqaIZaWmaaGaeiOla4IaeG4mamJaey4k % aSIaemOyaiMaeyypa0JaeyOeI0IaeGymaedabaGaeyi1HSTaeGOmai % Jaey4kaSIaemOyaiMaeyypa0JaeyOeI0IaeGymaedabaGaeyi1HSTa % emOyaiMaeyypa0JaeyOeI0IaeG4mamdaaaa!5E79! \begin{array}{l} I\left( {3; - 1} \right) \in d \Rightarrow \frac{2}{3}.3 + b = - 1\\ \Leftrightarrow 2 + b = - 1\\ \Leftrightarrow b = - 3 \end{array}\)

Vậy phương trình đường thẳng (d): 

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabdMha5jabg2da9maalaaabaGaeGOmaida % baGaeG4mamdaaiabdIha4jabgkHiTiabiodaZaqaaiabgsDiBlabdM % ha5jabg2da9maalaaabaGaeGOmaiJaemiEaGNaeyOeI0IaeGyoaKda % baGaeG4mamdaaaqaaiabgsDiBlabiodaZiabdMha5jabg2da9iabik % daYiabdIha4jabgkHiTiabiMda5aqaaiabgsDiBlabikdaYiabdIha % 4jabgkHiTiabiodaZiabdMha5jabg2da9iabiMda5aaaaa!6161! \begin{array}{l} y = \frac{2}{3}x - 3\\ \Leftrightarrow y = \frac{{2x - 9}}{3}\\ \Leftrightarrow 3y = 2x - 9\\ \Leftrightarrow 2x - 3y = 9 \end{array}\)

Chọn B.

TXĐ: \(D=\mathbb{R}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaacqGHaiIicqWG4baEcqGHiiIZcqWGebarcqGHshI3 % cqGHsislcqWG4baEcqGHiiIZcqWGebaraaa!4732! \forall x \in D \Rightarrow - x \in D\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabdAgaMnaabmaabaGaeyOeI0IaemiEaGha % caGLOaGaayzkaaGaeyypa0ZaaqWaaeaacqaIYaGmcqGGUaGldaqada % qaaiabgkHiTiabdIha4bGaayjkaiaawMcaaiabgUcaRiabigdaXaGa % ay5bSlaawIa7aiabgUcaRmaaemaabaGaeGymaeJaeyOeI0IaeGOmai % ZaaeWaaeaacqGHsislcqWG4baEaiaawIcacaGLPaaaaiaawEa7caGL % iWoaaeaacaaMc8UaaGPaVlaaykW7caaMc8UaaGPaVlaaykW7caaMc8 % UaaGPaVlaaykW7caaMc8UaaGPaVlaaykW7caaMc8UaaGPaVlaaykW7 % cqGH9aqpdaabdaqaaiabgkHiTiabikdaYiabdIha4jabgUcaRiabig % daXaGaay5bSlaawIa7aiabgUcaRmaaemaabaGaeGymaeJaey4kaSIa % eGOmaiJaemiEaGhacaGLhWUaayjcSdaabaGaaGPaVlaaykW7caaMc8 % UaaGPaVlaaykW7caaMc8UaaGPaVlaaykW7caaMc8UaaGPaVlaaykW7 % caaMc8UaaGPaVlaaykW7caaMc8Uaeyypa0ZaaqWaaeaacqaIXaqmcq % GHsislcqaIYaGmcqWG4baEaiaawEa7caGLiWoacqGHRaWkdaabdaqa % aiabikdaYiabdIha4jabgUcaRiabigdaXaGaay5bSlaawIa7aaqaai % aaykW7caaMc8UaaGPaVlaaykW7caaMc8UaaGPaVlaaykW7caaMc8Ua % aGPaVlaaykW7caaMc8UaaGPaVlaaykW7caaMc8UaaGPaVlabg2da9m % aaemaabaGaeGOmaiJaemiEaGNaey4kaSIaeGymaedacaGLhWUaayjc % SdGaey4kaSYaaqWaaeaacqaIXaqmcqGHsislcqaIYaGmcqWG4baEai % aawEa7caGLiWoaaeaacaaMc8UaaGPaVlaaykW7caaMc8UaaGPaVlaa % ykW7caaMc8UaaGPaVlaaykW7caaMc8UaaGPaVlaaykW7caaMc8UaaG % PaVlaaykW7cqGH9aqpcqWGMbGzdaqadaqaaiabdIha4bGaayjkaiaa % wMcaaaaaaa!EBB1! \begin{array}{l} f\left( { - x} \right) = \left| {2.\left( { - x} \right) + 1} \right| + \left| {1 - 2\left( { - x} \right)} \right|\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left| { - 2x + 1} \right| + \left| {1 + 2x} \right|\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left| {1 - 2x} \right| + \left| {2x + 1} \right|\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left| {2x + 1} \right| + \left| {1 - 2x} \right|\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = f\left( x \right) \end{array}\)

Vậy hàm số là hàm số chẵn.

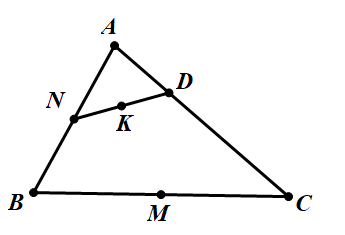
Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaadaGabaabaeqabaGaemiraqKaeyicI4SaemyqaeKa % em4qameabaGaemiraqKaem4qamKaeyypa0JaeGOmaiJaemiraqKaem % yqaeeaaiaawUhaaiabgkDiElabdgeabjabdseaejabg2da9maalaaa % baGaeGymaedabaGaeG4mamdaaiabdgeabjabdoeadbaa!508D! \left\{ \begin{array}{l} D \in AC\\ DC = 2DA \end{array} \right. \Rightarrow \overrightarrow{A D} = \frac{1}{3}\overrightarrow{A C}\)

Khi đó

\(\begin{aligned} \overrightarrow{A R} &=\frac{1}{2}(\overrightarrow{A N}+\overrightarrow{A D}) \\ &=\frac{1}{2}\left(\frac{1}{2} \overrightarrow{A B}+\frac{1}{3} \overrightarrow{A C}\right) \\ &=\frac{1}{4} \overrightarrow{A B}+\frac{1}{6} \overrightarrow{A C} \end{aligned}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabgkDiElabd2gaTjabg2da9maalaaabaGa % eGymaedabaGaeGinaqdaaiabcUda7iabd6gaUjabg2da9maalaaaba % GaeGymaedabaGaeGOnaydaaaqaaiabgkDiElabdsfaujabg2da9iab % isda0iabd2gaTjabgkHiTiabiAda2iabd6gaUjabg2da9iabisda0m % aalaaabaGaeGymaedabaGaeGinaqdaaiabgkHiTiabiAda2maalaaa % baGaeGymaedabaGaeGOnaydaaiabicdaWaaaaa!5A1C! \begin{array}{l} \Rightarrow m = \frac{1}{4};n = \frac{1}{6}\\ \Rightarrow T = 4m - 6n = 4\frac{1}{4} - 6\frac{1}{6}=0 \end{array}\)

Chọn D vì

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaaqaaaaaaaaaWdbmaaFiaapaqaa8qacqWGcbGqcqWG % dbWqaiaawEniaiabgUcaRmaaFiaapaqaa8qacqWGbbqqcqWGcbGqai % aawEniaiabg2da9maaFiaapaqaa8qacqWGcbGqcqWGdbWqaiaawEni % aiabgkHiTmaaFiaapaqaaiabdkeacjabdgeabbWdbiaawEniaiabg2 % da9maaFiaapaqaa8qacqWGbbqqcqWGdbWqaiaawEniaaaa!5298! \overrightarrow {BC} + \overrightarrow {AB} = \overrightarrow {BC} - \overrightarrow {BA} = \overrightarrow {AC} \)

AB = AC = a nên tam giác ABC cân tại A

Gọi M là trung điểm BC, khi đó \(AM\bot BC\) và AM là phân giác của góc BAC.

Ta có

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeWaaqWaaeaadaWhcaWdaeaa % peGaemyqaeKaemOqaieacaGLxdcacqGHRaWkdaWhcaWdaeaapeGaem % yqaeKaem4qameacaGLxdcaaiaawEa7caGLiWoacqGH9aqpdaabdaqa % aiabikdaYmaaFiaabaGaemyqaeKaemyta0eacaGLxdcaaiaawEa7ca % GLiWoacqGH9aqpcqaIYaGmcqGGUaGldaabdaqaamaaFiaabaGaemyq % aeKaemyta0eacaGLxdcaaiaawEa7caGLiWoacqGH9aqpcqaIYaGmcq % GGUaGlcqWGbbqqcqWGnbqtaeaacqWGbbqqcqWGnbqtcqGH9aqpcqWG % bbqqcqWGcbGqcqGGUaGlcyGGZbWCcqGGPbqAcqGGUbGBdaqiaaqaai % abdkeacjabdgeabjabd2eanbGaayPadaGaeyypa0JaemyyaeMaeiOl % a4Iagi4yamMaei4Ba8Maei4CamNaeGOnayJaeGimaaZaaWbaaSqabe % aacqaIWaamaaGccqGH9aqpdaWcaaqaaiabdggaHbqaaiabikdaYaaa % aeaacqGHshI3daabdaqaamaaFiaapaqaa8qacqWGbbqqcqWGcbGqai % aawEniaiabgUcaRmaaFiaapaqaa8qacqWGbbqqcqWGdbWqaiaawEni % aaGaay5bSlaawIa7aiabg2da9iabikdaYiabc6caUmaalaaabaGaem % yyaegabaGaeGOmaidaaiabg2da9iabdggaHbaaaa!90AD! \begin{array}{l} \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2.\left| {\overrightarrow {AM} } \right| = 2.AM\\ AM = AB.\sin \widehat {BAM} = a.\cos {60^0} = \frac{a}{2}\\ \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2.\frac{a}{2} = a \end{array}\)

Gọi D là trung điểm AC

Ta có:

\(\left| {\vec u} \right| = \left| {\overrightarrow {BA} + \overrightarrow {BC} } \right| = \left| {2\overrightarrow {BD} } \right| = 2\left| {\overrightarrow {BD} } \right|\)

Xét tam giác ABC vuông tại A có:

\(\begin{array}{l} BD = \sqrt {A{D^2} + A{B^2}} = \sqrt {{2^2} + {3^2}} = \sqrt {13} \\ \Rightarrow \left| {\vec u} \right| = 2\left| {\overrightarrow {BD} } \right| = 2\sqrt {13} \end{array}\)

ĐKXĐ:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaadaGabaabaeqabaGaemiEaGNaeyOeI0IaeGymaeJa % eyOpa4JaeGimaadabaGaeG4mamJaeyOeI0IaemiEaGNaeyyzImRaeG % imaadaaiaawUhaaiabgsDiBpaaceaaeaqabeaacqWG4baEcqGH+aGp % cqaIXaqmaeaacqWG4baEcqGHKjYOcqaIZaWmaaGaay5Eaaaaaa!5287! \left\{ \begin{array}{l} x - 1 > 0\\ 3 - x \ge 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x > 1\\ x \le 3 \end{array} \right.\)

Vậy \(D=(1,3]\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaadaWcaaqaaiabgkHiTiabdkgaIbqaaiabikdaYiab % dggaHbaacqGH9aqpdaWcaaqaaiabisda0aqaaiabikdaYaaacqGH9a % qpcqaIYaGmaaa!4479! \frac{{ - b}}{{2a}} = \frac{4}{2} = 2\)

Vậy x=2 là trục đối xứng của đồ thị hàm số.

do a=1>0 nên parabol có bể lõm quay lên, khi đó hàm số nghịch biến trên khoảng  \((-\infty, 2)\) và đồng biến trên khoảng \((2,+\infty)\)  

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabdgeabjabgQIiilabdkeacjabg2da9maa % jadabaGaeyOeI0IaeyOhIuQaei4oaSJaeyOeI0IaeGOmaidacaGLOa % GaayzxaaGaeyOkIG8aaKGeaeaacqaIZaWmcqGG7aWocqGHRaWkcqGH % EisPaiaawUfacaGLPaaaaeaacqGHshI3daqadaqaaiabdgeabjabgQ % IiilabdkeacbGaayjkaiaawMcaaiabgMIihlabdoeadjabg2da9iab % gwGigdaaaa!5B70! \begin{array}{l} A \cup B = \left( { - \infty ; - 2} \right] \cup \left[ {3; + \infty } \right)\\ \Rightarrow \left( {A \cup B} \right) \cap C = \emptyset \end{array}\)

A sai vì \(N \backslash M=(3,5)\)

Gọi A là tập hợp số học sinh giỏi Toán, B là tập hớp các học sinh giỏi Văn

Theo đề bài ta có

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabcYha8jabdgeabjabcYha8jabg2da9iab % igdaXiabicdaWaqaaiabcYha8jabdkeacjabcYha8jabg2da9iabig % daXiabiwda1aqaaiabcYha8jabdgeabjabgMIihlabdkeacjabcYha % 8jabg2da9iabiwda1aaaaa!51A2! \begin{array}{l} |A| = 10\\ |B| = 15\\ |A \cap B| = 5 \end{array}\)

Số học sinh giỏi Toán, Văn là:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeGaemOBa4MaeiikaGIaemyq % aeKaeyOkIGSaemOqaiKaeiykaKIaeyypa0JaemOBa4MaeiikaGIaem % yqaeKaeiykaKIaey4kaSIaemOBa4MaeiikaGIaemOqaiKaeiykaKIa % eyOeI0IaemOBa4MaeiikaGIaemyqaeKaeyykICSaemOqaiKaeiykaK % cabaGaeyypa0JaeGymaeJaeGimaaJaey4kaSIaeGymaeJaeGynauJa % eyOeI0IaeGynauJaeyypa0JaeGOmaiJaeGimaadaaaa!5E53! \begin{array}{l} n(A \cup B) = n(A) + n(B) - n(A \cap B)\\ = 10 + 15 - 5 = 20 \end{array}\)

Số học sinh của lớp là:20+17=37 học sinh

các tập hợp con có hai phân tử là: 

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakeaadaGadaqaaiabicdaWiabcUda7iabikdaYaGaay5E % aiaaw2haaiabcUda7maacmaabaGaeGimaaJaei4oaSJaeG4mamdaca % GL7bGaayzFaaGaei4oaSZaaiWaaeaacqaIWaamcqGG7aWocqaI0aan % aiaawUhacaGL9baacqGG7aWodaGadaqaaiabikdaYiabcUda7iabio % daZaGaay5Eaiaaw2haaiabcUda7maacmaabaGaeGOmaiJaei4oaSJa % eGinaqdacaGL7bGaayzFaaGaei4oaSZaaiWaaeaacqaIZaWmcqGG7a % WocqaI0aanaiaawUhacaGL9baaaaa!5E6A! \left\{ {0;2} \right\};\left\{ {0;3} \right\};\left\{ {0;4} \right\};\left\{ {2;3} \right\};\left\{ {2;4} \right\};\left\{ {3;4} \right\}\)

Ta có

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabgkHiTiabikdaYiabgYda8iabikdaYiab % gkDiElabdAgaMnaabmaabaGaeyOeI0IaeGOmaidacaGLOaGaayzkaa % Gaeyypa0ZaaeWaaeaacqGHsislcqaIYaGmaiaawIcacaGLPaaadaah % aaWcbeqaaiabikdaYaaakiabgkHiTiabiodaZmaabmaabaGaeyOeI0 % IaeGOmaidacaGLOaGaayzkaaGaey4kaSIaeGymaeJaeyypa0JaeGym % aeJaeGymaedabaGaeGinaqJaeyOpa4JaeGOmaiJaeyO0H4TaemOzay % 2aaeWaaeaacqaI0aanaiaawIcacaGLPaaacqGH9aqpqaaaaaaaaaWd % bmaalaaapaqaa8qadaGcaaWdaeaapeGaeGinaqJaey4kaSIaeGOmai % daleqaaOGaeyOeI0IaeG4mamdapaqaa8qacqaI0aancqGHRaWkcqaI % XaqmaaGaeyypa0ZaaSaaaeaadaGcaaqaaiabiAda2aWcbeaakiabgk % HiTiabiodaZaqaaiabiwda1aaaaeaacqGHshI3cqWGMbGzdaqadaqa % aiabgkHiTiabikdaYaGaayjkaiaawMcaaiabgUcaRiabiwda1iabdA % gaMnaabmaabaGaeGinaqdacaGLOaGaayzkaaGaeyypa0JaeGymaeJa % eGymaeJaey4kaSIaeGynauZaaSaaaeaadaGcaaqaaiabiAda2aWcbe % aakiabgkHiTiabiodaZaqaaiabiwda1aaacqGH9aqpcqaIXaqmcqaI % XaqmcqGHRaWkdaGcaaqaaiabiAda2aWcbeaakiabgkHiTiabiodaZi % abg2da9iabiIda4iabgUcaRmaakaaabaGaeGOnaydaleqaaaaaaa!8D38! \begin{array}{l} - 2 < 2 \Rightarrow f\left( { - 2} \right) = {\left( { - 2} \right)^2} - 3\left( { - 2} \right) + 1 = 11\\ 4 > 2 \Rightarrow f\left( 4 \right) = \frac{{\sqrt {4 + 2} - 3}}{{4 + 1}} = \frac{{\sqrt 6 - 3}}{5}\\ \Rightarrow f\left( { - 2} \right) + 5f\left( 4 \right) = 11 + 5\frac{{\sqrt 6 - 3}}{5} = 11 + \sqrt 6 - 3 = 8 + \sqrt 6 \end{array}\)

ĐKXĐ: \(x-m\ne 0\Leftrightarrow x\ne m\)

Hàm số xác định trên (-1;2)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeGaeyi1HSTaemyBa0Maeyyc % I88aaeWaaeaacqGHsislcqaIXaqmcqGG7aWocqaIYaGmaiaawIcaca % GLPaaaaeaacqGHuhY2daWabaabaeqabaGaemyBa0MaeyipaWJaeyOe % I0IaeGymaedabaGaemyBa0MaeyOpa4JaeGOmaidaaiaawUfaaaaaaa!50BD! \begin{array}{l} \Leftrightarrow m \notin \left( { - 1;2} \right)\\ \Leftrightarrow \left[ \begin{array}{l} m \le - 1\\ m \ge 2 \end{array} \right. \end{array}\)

Theo lý thuyết, điều kiện để mệnh đề \(P \Rightarrow Q\) sai là P đúng Q sai 

Chọn C vì thế x=-1, y=6 vao phương trình ta có

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeGaeGOnayJaeyypa0JaeGOm % aiZaaeWaaeaacqGHsislcqaIXaqmaiaawIcacaGLPaaapaWaaWbaaS % qabeaapeGaeGOmaidaaOGaeyOeI0IaeGinaqJaeiiFaWNaeyOeI0Ia % eGymaeJaeyOeI0IaeGymaeJaeiiFaWNaey4kaSIaeGymaeJaeGOmai % dabaGaeyi1HSTaeGOnayJaeyypa0JaeGOmaiJaeyOeI0IaeGinaqJa % eiOla4IaeGymaeJaey4kaSIaeGymaeJaeGOmaidabaGaeyi1HSTaeG % OnayJaeyypa0JaeGOnayZaaeWaaeaacqWGSbaBcqWGSbaBcqWGKbaz % aiaawIcacaGLPaaaaaaa!64E0! \begin{array}{l} 6 = 2{\left( { - 1} \right)^2} - 4| - 1 - 1| + 12\\ \Leftrightarrow 6 = 2 - 4.1 + 12\\ \Leftrightarrow 6 = 6\left( {lld} \right) \end{array}\)

Vậy điểm (-1;6) thuộc đồ thị hàm số.

Chọn D vì: Xét hàm số \(y=x^{3}-x\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaiabdsfaujabdIfayjabbseaejabcQda6iab % dseaejabg2da9iabdkfasbqaaiabgcGiIiabdIha4jabgIGiolabds % eaejabgkDiElabgkHiTiabdIha4jabgIGiolabdseaebqaaiabdAga % MnaabmaabaGaeyOeI0IaemiEaGhacaGLOaGaayzkaaGaeyypa0Zaae % WaaeaacqGHsislcqWG4baEaiaawIcacaGLPaaadaahaaWcbeqaaiab % iodaZaaakiabgkHiTmaabmaabaGaeyOeI0IaemiEaGhacaGLOaGaay % zkaaGaeyypa0JaeyOeI0IaemiEaG3aaWbaaSqabeaacqaIZaWmaaGc % cqGHRaWkcqWG4baEcqGH9aqpcqGHsisldaqadaqaaiabdIha4naaCa % aaleqabaGaeG4mamdaaOGaeyOeI0IaemiEaGhacaGLOaGaayzkaaGa % eyypa0JaeyOeI0IaemOzay2aaeWaaeaacqWG4baEaiaawIcacaGLPa % aaaaaa!74F5! \begin{array}{l} TX{\rm{Đ}}:D = \mathbb{R}\\ \forall x \in D \Rightarrow - x \in D\\ f\left( { - x} \right) = {\left( { - x} \right)^3} - \left( { - x} \right) = - {x^3} + x = - \left( {{x^3} - x} \right) = - f\left( x \right) \end{array}\)Vậy hàm số là hàm số lẻ.

Gọi M là trung điểm BC

G là trọng tâm tam giác ABC nên:

\( \begin{array}{l} \overrightarrow {AG} = 2\overrightarrow {GM} \\ \text{Khi đó }\left| {\overrightarrow {AB} - \overrightarrow {CG} } \right|\\ = \left| {\overrightarrow {AG} + \overrightarrow {GB} - \overrightarrow {CG} } \right|\\ = \left| {\overrightarrow {AG} + \overrightarrow {GB} + \overrightarrow {GC} } \right|\\ = \left| {\overrightarrow {AG} + 2\overrightarrow {GM} } \right|\\ = \left| {\overrightarrow {AG} + \overrightarrow {AG} } \right| = \left| {2\overrightarrow {AG} } \right|\\ = 2\left| {\overrightarrow {AG} } \right| = 2.AG\\ = 2.\frac{2}{3}AM = \frac{4}{2}AM = \frac{4}{3}\frac{{a\sqrt 3 }}{2} = \frac{{2a\sqrt 3 }}{2} \end{array}\)

B\A là tập hợp những phần tử thuộc B nhưng không thuộc A. Vậy 

\(B \backslash A=\{2,3,6\}\)

theo tính chất hình bình hành ta có \(\overrightarrow{A B}+\overrightarrow{A D}=\overrightarrow{AC}\)

ĐKXĐ:

\(\begin{array}{l} {x^2} - 4x + 3 > 0\\ \left( {x - 3} \right)\left( {x - 1} \right) > 0 \end{array}\)

TH1: 

\(\left\{ \begin{array}{l} x - 3 > 0\\ x - 1 > 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x > 3\\ x > 1 \end{array} \right. \Leftrightarrow x > 3\)

TH2:

\(\left\{ \begin{array}{l} x - 3 < 0\\ x - 1 < 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x < 3\\ x < 1 \end{array} \right. \Leftrightarrow x < 1\)

Kết hợp hai trường hợp ta có x>3 hoặc x<1

hay \(x \in(-\infty, 1) \cup(3,+\infty)\)

\(\begin{array}{l} \text{Ta có }\frac{{4x + 7}}{{x + 1}} = \frac{{4\left( {x + 1} \right) - 4 + 7}}{{x + 1}} = \frac{{4\left( {x + 1} \right) + 3}}{{x + 1}}\\ = \frac{{4\left( {x + 1} \right)}}{{x + 1}} + \frac{3}{{x + 1}}\\ = 4 + \frac{3}{{x + 1}}\\ Để\,\,\frac{{4x + 7}}{{x + 1}} \in Z\,\,thì\,\,\frac{3}{{x + 1}} \in Z\\ ĐK:x + 1 \ne 0 \Leftrightarrow x \ne - 1\\ \text{khi đó: }\frac{3}{{x + 1}} \in Z \Leftrightarrow \left( {x + 1} \right) \in U\left( 3 \right) = \left\{ {1; - 1;3; - 3} \right\}\\ x + 1 = 1 \Leftrightarrow x = 0\left( n \right)\\ x + 1 = - 1 \Leftrightarrow x = - 2\left( n \right)\\ x + 1 = 3 \Leftrightarrow x = 2\left( n \right)\\ x + 1 = - 3 \Leftrightarrow x = - 4\left( n \right) \end{array}\)

Vậy \(A = \left\{ {1; - 2;2; - 4} \right\}\)

Vậy tập hợp con có 3 phân tử của A là 

\(\left\{ {1; - 2;2} \right\};\left\{ {1; - 2; - 4} \right\};\left\{ {1;2; - 4} \right\};\left\{ { - 2;3; - 4} \right\}\)

\(\begin{array}{l} B \subset A\\ \Leftrightarrow \left\{ \begin{array}{l} a \le 5\\ 6 \le a + 2 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} a \le 5\\ a \ge 4 \end{array} \right.\\ \Leftrightarrow 4 \le a \le 5 \end{array}\)

Hoành độ đỉnh Parabol: 

\(\begin{array}{l} x = \frac{{ - b}}{{2a}}\\ \Leftrightarrow x = \frac{4}{2}\\ \Leftrightarrow x = 2 \end{array}\)

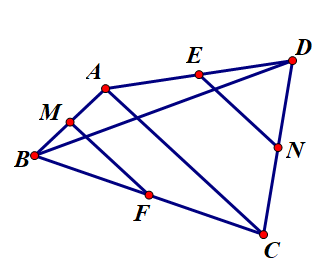
Gọi E,F là trung điểm AD, BC. Ta có

+MF là đường trung bình của tam giác ABC 

\(\left\{ \begin{array}{l} MF//AC\\ MF = \frac{1}{2}AC \end{array} \right.\)

+EN là đường trung bình của tam giác ADC 

\(\Rightarrow \left\{ \begin{array}{l} EN//AC\\ EN = \frac{1}{2}AC \end{array} \right.\)

\(\Rightarrow \left\{ \begin{array}{l} MF//EN\\ MF = EN \end{array} \right. \Rightarrow \)MENF là hình bình hành

+ME là đường trung bình của tam giác ABD 

\(\Rightarrow \left\{ \begin{array}{l} ME//BD\\ ME = \frac{1}{2}BD \end{array} \right. \Rightarrow \overrightarrow {BD} = 2\overrightarrow {ME} \)

Khi đó ta có

\(\begin{array}{l} \overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MF} + 2\overrightarrow {ME} \\ = 2\left( {\overrightarrow {MF} + \overrightarrow {ME} } \right)\\ = 2\overrightarrow {MN} \end{array}\)

Gọi A, B lần lượt là tập hợp các học sinh học Tiếng Nga, Đức. Khi đó

\(\begin{array}{l} \left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right|\\ = 25 + 20 - 10 = 35 \end{array}\)

\(\begin{array}{l} {+\rm{f(x) = |x + 2| - |x - 2|}}\\ {\rm{TXD}}:D = R\\ \forall x \in D \Rightarrow - x \in D\\ f\left( { - x} \right) = {\rm{| - x + 2| - | - x - 2| = | - }}\left( {{\rm{x - 2}}} \right){\rm{| - | - }}\left( {{\rm{x + 2}}} \right){\rm{|}}\\ {\rm{ = |x - 2| - |x + 2| = - }}\left( {{\rm{|x + 2| - |x - 2|}}} \right) = - f\left( x \right)\\ \Rightarrow \text{f(x) là hàm số lẻ} \\ {+\rm{ g(x) = - | x|}}\\ {\rm{TXD}}:D = R\\ \forall x \in D \Rightarrow - x \in D\\ {\rm{ g( - x) = - | - x| = - | x|}} = g\left( x \right)\\ \Rightarrow \text{f(x) là hàm số chẵn} \end{array}\)

Các tập hợp con có hai phần tử của A là 

\(\left\{ {0;2} \right\};\left\{ {0;5} \right\};\left\{ {0;8} \right\};\left\{ {2;5} \right\};\left\{ {2;8} \right\};\left\{ {5;8} \right\}\)

Vậy có tất cả 6 tập hợp con cần tìm.

Do \({\rm{[ - 1,2)}} \subset R\) nên phân bù của \([-1,2)\) trong \(\mathbb{R}\) là

\(R\backslash {\rm{[ - 1,2)}} = \left( { - \infty ; - 1} \right) \cup \left[ {2; + \infty } \right)\)

Ta có

\(\begin{array}{l} A = \left( { - \infty ;3} \right)\\ B = \left( {1;5} \right]\\ C = \left[ { - 2;4} \right]\\ \Rightarrow B \cup C = \left[ { - 2;5} \right]\\ A \cap C = \left[ { - 2;3} \right)\\ \Rightarrow \left( {B \cup C} \right)\backslash \left( {A \cap C} \right) = \left[ {3;5} \right] \end{array}\)

ĐKXĐ:

\(\begin{array}{l} \left\{ \begin{array}{l} x - 1 \ge 0\\ x - 2\sqrt {x - 1} \ge 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x \ge 1\\ x - 1 - 2\sqrt {x - 1} + 1 \ge 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x \ge 1\\ {\left( {\sqrt {x - 1} - 1} \right)^2} \ge 0\left( {lld} \right) \end{array} \right.\\ \Leftrightarrow x \ge 1 \end{array}\)

Vậy \(\begin{array}{lll} D=[1,+\infty) \end{array}\)

\(A = \left\{ {0;1;2;3} \right\}\)

\(A \cap B\) là tập hợp những phần tử thuộc A và thuộc B

Vậy \(A \cap B=\{0,1,2,3\}\)