Đề thi giữa HK1 môn Toán 10 năm 2020 - Trường THPT Lý Thường Kiệt
-
Hocon247
-
40 câu hỏi
-
60 phút
-
59 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho đoạn thẳng AB có I là trung điểm. Mệnh đề nào dưới đây sai?
.png)
D sai vì \(\overrightarrow {IA}\,\,và\,\, \overrightarrow {IB} \) ngược hướng nên không thỏa điều kiện cùng hướng của hai vec tơ bằng nhau
Cho ba điểm A, B, C tùy ý. Mệnh đề nào dưới đây đúng?
Theo định nghĩa cộng hai vectơ ta có \(\overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{B C}\)
Nghiệm của hệ phương trình \(\left\{\begin{array}{l} x-y=3 \\ 2 x+y=3 \end{array}\right.\) là
Ta có
\(\begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {x - y = 3}\\ {2x + y = 3} \end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x = 3 + y}\\ {2(3 + y) + y = 3} \end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x = 3 + y}\\ {3y = - 3} \end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x = 2}\\ {y = - 1} \end{array}} \right. \end{array}\)
Cho hình vuông ABCD có cạnh bằng \(\sqrt2\) . Tính \(T=|\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D}|\)
Ta có
\(\begin{array}{l} T = |\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} |\\ = |\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AC} |\\ = |\overrightarrow {AC} + \overrightarrow {AC} | = 2|\overrightarrow {AC} | = 2.\sqrt 2 .\sqrt 2 = 4 \end{array}\)
Tập hợp tất cả các giá trị của tham số m để hàm số \(y=(m-1) x+m-2\) đồng biến trên \(\mathbb{R}\) là
Áp dụng hàm số \(y=(m-1) x+m-2\) đồng biến trên \(\mathbb{R}\) khi và chỉ khi
\(\begin{array}{l} a = m - 1 > 0\\ \Leftrightarrow m > 1 \end{array}\)
Cho hàm số \(y=f(x)=\left\{\begin{array}{lll} x-1 & \text { vói } & x \geq 1 \\ x^{2}+2 & \text { vói } & x<1 \end{array}\right.\). Tính\(f(-2)+f(2)\)
Ta có
\(\begin{array}{l} - 2 < 1 \Rightarrow f( - 2) = {( - 2)^2} + 2 = 6\\ 2 > 1 \Rightarrow f(2) = 2 - 1 = 1\\ \Rightarrow f( - 2) + f(2) = 6 + 1 = 7 \end{array}\)
Bạn Minh Thi vừa thi đậu vào lớp 10 năm học 2019 – 2020, ba mẹ của bạn thưởng cho bạn một chiếc laptop. Khi mang về bạn phát hiện ngoài bao bì có ghi trọng lượng 1,5456 kg ± 0,001 kg. Giá trị quy tròn trọng lượng của chiếc laptop đó là
Độ chính xác đến hang phần nghìn (0,001) nên ta quy tròn 1,5456 đến hàng phần trăm:
Số quy tròn là 1,55
Cho parabol \(y=a x^{2}+b x+3\) có đỉnh \(I(2 ;-2)\) Khi đó giá trị a+2b bằng
Đỉnh I(2;-2) nên \({x_I} = 2;{y_I} = - 2\)
Khi đó ta có:
\(\begin{array}{l} \left\{ \begin{array}{l} \frac{{ - b}}{{2a}} = 2\\ a{.2^2} + b.2 + 3 = - 2 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} -b = 4a\\ 4a +2b = -5 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} b =-5\\ a = \frac{{ -5}}{4} \end{array} \right.\\ \Rightarrow a + 2b = \frac{{ 35}}{4} \end{array}\)
Cho hai tập hợp A = (- 20 ; 20) và \(B=[2 m-4 ; 2 m+2)\) ( m là tham số). Có tất cả bao nhiêu giá trị nguyên của tham số m để \(A \cup B=A ?\)
\(A \cup B=A \) khi
\(\begin{array}{l} B \subset A\\ \Leftrightarrow \left\{ \begin{array}{l} 2m - 4 > - 20\\ 2m + 2 < 20 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m > - 8\\ m < 9 \end{array} \right. \end{array}\)
Do m nguyên nên \(m\in\{-7;-6;-5;-4;...;5;6;7;8\}\)
Vậy có tất cả 16 giá trị m thỏa yêu cầu.
Tìm tất cả các giá trị của m để hàm số \(y=\left(m^{4}-1\right) x+2020\) là hàm số bậc nhất?
Hàm số là hàm số bậc nhất \( \Leftrightarrow {m^4} - 1 \ne 0 \Leftrightarrow \left\{ \begin{array}{l} m \ne 1\\ m \ne - 1 \end{array} \right.\)
Điều kiện của a b , để phương trình \(a x+b=0,(a, b \in \mathbb{R})\)vô nghiệm là
Ta có \(ax + b = 0 \Leftrightarrow ax = - b\)
Phương trình vô nghiệm \( \Leftrightarrow \left\{ \begin{array}{l} a = 0\\ b \ne 0 \end{array} \right.\)
Cho tam giác ABC , điểm M thỏa mãn:\(2\overrightarrow{M A}-3 \overrightarrow{M B}=\overrightarrow{0}\). Khi đó, với điểm I bất kỳ, thỏa mãn\(\overrightarrow{I A}=m \overrightarrow{I M}+n \overrightarrow{I B}\) thì cặp số (m; n) bằng
\(\begin{array}{l} 2\overrightarrow {MA} - 3\overrightarrow {MB} = \vec 0\\ \Leftrightarrow 2\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right) - 3\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right) = \overrightarrow 0 \\ \Leftrightarrow - \overrightarrow {MI} + 2\overrightarrow {IA} - 3\overrightarrow {IB} = \overrightarrow 0 \\ \Leftrightarrow 2\overrightarrow {IA} = \overrightarrow {MI} + 3\overrightarrow {IB} \\ \Leftrightarrow \overrightarrow {IA} = \frac{1}{2}\overrightarrow {MI} + \frac{3}{2}\overrightarrow {IB} \\ \Leftrightarrow \overrightarrow {IA} = - \frac{1}{2}\overrightarrow {IM} + \frac{3}{2}\overrightarrow {IB} \end{array}\)
Tập hợp \(X=\{1 ; 2 ; 3\}\) có bao nhiêu tập con?
Tập X có 3 phần tử nên số tập con là \(2^3=8\)
Cho \(A=(-\infty ;-2], B=[3 ;+\infty), C=(0 ; 4)\) Khi đó tập \((A \cup B) \cap C\) là:
Theo định nghĩa phép hợp ta có
\((A \cup B)=(-\infty ;-2]\cup[3 ;+\infty)\)
Vậy \((A \cup B) \cap C=[3;4)\)
Cho tam giác ABC cân tại A ,\(\widehat{B A C}=120^{\circ} \text { và } A B=a\). Tính \(\overrightarrow{B A} \cdot\overrightarrow{C A}\)
Ta có
\(\begin{array}{l} \cos \widehat {BAC} = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{|\overrightarrow {BA} |.|\overrightarrow {BC} |}}\\ \Leftrightarrow \overrightarrow {BA} .\overrightarrow {BC} = |\overrightarrow {BA} |.|\overrightarrow {BC} |.\cos \widehat {BAC} = a.a.\cos {120^0} = \frac{{ - {a^2}}}{2} \end{array}\)
Cho \(\vec{u}=(1 ;-3), \vec{v}=(2 ; 5)\). Khi đó tích vô hướng \(\overrightarrow{u}.\vec v\)bằng
Ta có \(\overrightarrow{u}.\vec v=x_u.x_v+y_u.y_v=-13\)
Phủ định mệnh đề “có một học sinh của lớp 10A không thích học môn toán” là
Theo định nghĩa mệnh đề thì phủ định của mệnh đề đã cho là "Tất cả các bạn lớp 10A đều thích học môn toán."
Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?

hình vẽ thể hiện tập hợp các số sao cho \(x<2 \) hoặc \(x\ge 5\) nên chọn B
Cho điểm \(M(1 ;-3), N(-2 ; 1)\) Khi đó độ dài đoạn MN bằng
\(\begin{array}{l} MN = \sqrt {{{\left( {{x_M} - {x_N}} \right)}^2} + {{\left( {{y_M} - {y_N}} \right)}^2}} \\ = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5 \end{array}\)
Cho hàm số \(y=a x^{2}-b x+c(a \neq 0)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng
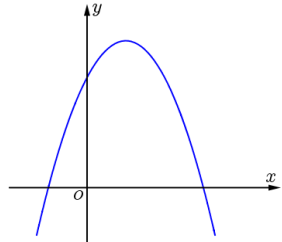
Đồ thị hàm số cắt trục tung tại điểm nằm trên trục Ox nên c>0
Đồ thị hàm số có bề lõm hướng xuống nên a<0
Đồ thị hàm số có đỉnh I nằm trên trục Ox nên \(x_I=\frac{-b}{2a}>0\), mà a<0 nên b>0
Tập xác định của hàm số \(y=\frac{x+1}{x-1}\) là
ĐKXĐ: \(x-1\ne 0\Leftrightarrow x\ne 1\)
Cho hàm số \(y=x^{2}-2 x-3\) . Tìm khẳng định SAI?
\({x_I} = \frac{{ - b}}{{2a}} = 1\)
Hàm số có a=1>0 nên bề lõm quay lên.
Vậy hàm số đồng biến trên \((1;+\infty)\), nghịch biến trên \((-\infty ; 1)\)
Vậy B sai
Đồ thị hàm số \(y=x^{2}-2 x+m\), với m là tham số, cắt trục hoành tại hai điểm phân biệt khi
Phương tình hoành độ giao điểm: \(x^{2}-2 x+m=0 (*)\)
Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt \(\Leftrightarrow\) phương trình (*) có hai nghiệm phân biệt.
\(\begin{array}{l} \Delta = {\left( { - 2} \right)^2} - 4.1.m = 4 - 4m > 0\\ \Leftrightarrow m < 1 \end{array}\)
Điểm M(1;2) không thuộc đồ thị hàm số nào sau đây?
Chọn C vì thế tọa độ điểm M vào ta có
\(x=1\Rightarrow y=x+2=3\ne 2\)
Cho tam giác ABC , có bao nhiêu điểm M thỏa mãn \(|\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}|=3 ?\)
Ta có
\(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}=3\overrightarrow{M G}\) với G là tọng tâm tam giác ABC.
Khi đó \(|\overrightarrow{M G}|=3\Leftrightarrow \) M thuộc đường tròn tâm G, bán kính bằng 3. Vậy có vô số điểm M thỏa mãn điều kiện.
Cho hình vuông ABCD, có cạnh bằng a . Khi đó \(|\overrightarrow{A D}+\overrightarrow{A C}|\) bằng
Gọi M là trung điểm CD. Khi đó
\(\begin{array}{l} |\overrightarrow {AD} + \overrightarrow {AC} | = |2\overrightarrow {AM} | = 2.|\overrightarrow {AM} |\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2.\sqrt {A{D^2} - D{M^2}} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2.\sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = 2.\frac{{a\sqrt 5 }}{2} = a\sqrt 5 \end{array}\)
Biết rằng hai vectơ \(\vec a\) và \(\vec b \) không cùng phương nhưng hai vectơ \(3 \vec{a}-2 \vec{b} \text { và } \vec{a}+(x-1) \vec{b}\)cùng phương. Khi đó giá trị của x là
\(3 \vec{a}-2 \vec{b} \text { và } \vec{a}+(x-1) \vec{b}\) cùng phương khi
\(\frac{3}{1} = \frac{{ - 2}}{{x - 1}} \Leftrightarrow 3\left( {x - 1} \right) = - 2 \Leftrightarrow x = \frac{1}{3}\)
Phương trình \(|x+1|=x^{2}-x\) có bao nhiêu nghiệm?
Ta có
\(\begin{array}{l} |x + 1| = {x^2} - x\\ \Leftrightarrow \left[ \begin{array}{l} x + 1 = {x^2} - x\\ x + 1 = - \left( {{x^2} - x} \right) \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x + 1 = {x^2} - x\\ x + 1 = - \left( {{x^2} - x} \right)\text{(vô nghiệm)} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 1 - \sqrt 2 \\ x = 1 + \sqrt 2 \end{array} \right. \end{array}\)
Cho điểm \(A(1 ;-2) ; B(1 ; 1) ; C(-1 ;-1)\)thành lập thành tam giác. Khi đó góc \(\widehat{A B C}\) bằng
Ta có
\(\begin{array}{l} \overrightarrow {BA} \left( {0;-3} \right);AB = \sqrt {{0^2} + {3^2}} = 3\\ \overrightarrow {AC} \left( { - 2;1} \right);AC = \sqrt {{{\left( { - 2} \right)}^2} + {1^2}} = \sqrt 5\\ \overrightarrow {BC} \left( { - 2; - 2} \right);BC = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 8 \end{array}\)
Khi đó
\(\begin{array}{l} \cos \left( {\overrightarrow {AB} ;\overrightarrow {BC} } \right) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{|\overrightarrow {BA} |.|\overrightarrow {BC} |}} = \frac{6}{{3\sqrt 8 }} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \widehat {ABC} = {45^O} \end{array}\)
Cho hai điểm \(A(-3,2), B(4,3)\) Điểm C thuộc trục Ox và có hoành độ dương để tam giác CAB vuông tại C . Khi đó tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành?
C thuộc Ox nên C(x;0)
\(\overrightarrow {AC} \left( {x + 3; - 2} \right);\overrightarrow {CB} \left( {x - 4; - 3} \right)\)
Tam giác CAB vuông tại C
\(\begin{array}{l} \Leftrightarrow \overrightarrow {CA} .\overrightarrow {CB} = 0\\ \Leftrightarrow \left( {x + 3} \right)\left( {x - 4} \right) + 6 = 0\\ \Leftrightarrow {x^2} - x - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = 3\left( n \right)\\ x = - 2\left( l \right) \end{array} \right. \Rightarrow C\left( {3;0} \right) \end{array}\)
\(\overrightarrow {CB}=(-1;-3)\)
gọi \(D(x_D;y_D), \overrightarrow {DA}=(x_D+3;y_D-2)\)
ABCD là hình bình hành
\(\begin{array}{l} \overrightarrow {CB} = \overrightarrow {DA} \\ \Leftrightarrow \left\{ \begin{array}{l} - 1 = {x_D} + 3\\ - 3 = {y_D}-2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {x_D} = -4\\ {y_D} = - 1 \end{array} \right. \end{array}\)
Trong mặt phẳng Oxy , cho tam giác ABC có G là trọng tâm của tam giác, biết rằng\(A(1 ; 1), B(1 ;-2), G(2 ; 3)\) tọa độ của điểm C là:
Ta có G là trọng tâm tam giác ABC nên ta có
\(\left\{ \begin{array}{l} {x_C} = 3{x_G} - {x_A} - {x_B} = 3.2 - 1 - 1 = 4\\ {y_C} = 3{y_G} - {y_A} - {y_B} = 3.3 - 1 + 2 = 10 \end{array} \right.\)
Vậy C(4;10)
Tổng các nghiệm của phương trình \(\sqrt{x^{2}-x}=1\) bằng
Ta có
\(\begin{array}{l} \sqrt {{x^2} - x} = 1\\ \Leftrightarrow {x^2} - x = 1 \Leftrightarrow {x^2} - x - 1 \end{array}\)
Phương trình có hai nghiệm, theo định lí Viét, tổng hai nghiệm là:
\({x_1} + {x_2} = \frac{{ - b}}{a} = \frac{1}{1} = 1\)
Cho \(A(2 ; 5), B(1 ; 3), C(5 ;-1)\). Tìm tọa độ điểm K sao cho \(\overrightarrow{A K}=3 \overrightarrow{B C}+2 \overrightarrow{C K}\)
Ta có
\(\begin{array}{l} \overrightarrow {BC} = \left( {4; - 4} \right);\overrightarrow {AK} = \left( {x - 2;y - 5} \right);\overrightarrow {CK} = \left( {x - 5;y + 1} \right)\\ \overrightarrow {AK} = 3\overrightarrow {BC} + 2\overrightarrow {CK} \\ \Leftrightarrow \left( {x - 2;y - 5} \right) = 3\left( {4; - 4} \right) + 2\left( {x - 5;y + 1} \right)\\ \Leftrightarrow \left( {x - 2;y - 5} \right) = \left( {2x + 2;2y - 10} \right)\\ \Leftrightarrow \left\{ \begin{array}{l} x - 2 = 2x + 2\\ y - 5 = 2y - 10 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x = -4\\ y = 5 \end{array} \right. \end{array}\)
Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình \(\frac{x-2}{x+m}=\frac{x}{x-1}\) vô nghiệm. Tổng tất cả các phần tử của S bằng
ĐK:\(x\ne -m\text{ và } x\ne 1\)
\(\begin{array}{l} \frac{{x - 2}}{{x + m}} = \frac{x}{{x - 1}}\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) = x\left( {x + m} \right)\\ \Leftrightarrow {x^2} - 3x + 2 = {x^2} + mx\\ \Leftrightarrow - \left( {3 + m} \right)x = - 2\\ \Leftrightarrow \left( {3 + m} \right)x = - 2 \end{array}\)
Phương trình vô nghiệm
\(\left\{ \begin{array}{l} a = 3 + m = 0\\ b = - 2 \ne 0\left( {lld} \right) \end{array} \right. \Leftrightarrow m = - 3\)
Vậy S={-3}, tổng các phần tử là -3
Cho hàm số bậc hai \(y=a x^{2}-b x+c\) có đồ thị là (P). Biết rằng (P) có tọa độ đỉnh I (1;1988) và đi qua điểm M (3;2020). Khi đó, a+b+c bằng?
I là đỉnh nên ta có
\(\begin{array}{l} \frac{b}{{2a}} = 1 \Leftrightarrow b = 2a \Leftrightarrow 2a - b = 0\,\,\,(1)\\ I \in \left( P \right) \Rightarrow a{.1^2} - b.1 + c = 1988 \Leftrightarrow a - b + c = 1988\,\,\,(2)\\ M \in \left( P \right) \Rightarrow a{.3^2} - b.3 + c = 2020 \Leftrightarrow 9a - 3b + c = 2020\,\,\,(3) \end{array}\)
từ (1), (2), (3) ta có hệ
\(\begin{array}{l} \left\{ \begin{array}{l} 2a - b = 0\\ a - b + c = 1988\\ 9a - 3b + c = 2020 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 8\\ b = 16\\ c = 1996 \end{array} \right.\\ \Rightarrow a + b + c = 2020 \end{array}\)
Hàm số \(f(x)=-x+|x+2|-|x-2| \) là
TXĐ: \(D=\mathbb{R}\)
\(\begin{array}{l} \forall x \in D \Rightarrow - x \in D\\ f\left( { - x} \right) = - \left( { - x} \right) + \left| { - x + 2} \right| - \left| { - x - 2} \right|\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = x + \left| { - \left( {x - 2} \right)} \right| - \left| { - \left( {x + 2} \right)} \right|\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = x + \left| {x - 2} \right| - \left| {x + 2} \right|\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \left( { - x - \left| {x - 2} \right| + \left| {x + 2} \right|} \right) = - f(x) \end{array}\)
Vậy hàm số là hàm số lẽ
Đường thẳng \(y=x-1\) và đồ thị hàm số \(y=x^{3}-x^{2}+x-1\) có hai điểm chung. Tìm tổng tung độ các giao điểm đó
Phương trình hoành độ giao điểm:
\(\begin{array}{l}
x^{3}-x^{2}+x-1=x-1 \\
\Leftrightarrow x^{3}-x^{2}=0 \Leftrightarrow x^{2}(x-1)=0 \\
\Leftrightarrow x_{1}=0 \text { hoặc } x_{2}=1
\end{array}\)
Tổng tung độ các điểm chung:
\(\begin{array}{l}
y_{1}+y_{2}=x_{1}-1+x_{2}-1 \\
=x_{1}+x_{2}-2=0+1-2=-1
\end{array}\)
Trong các hàm số sau, hàm số nào có tập giá trị là đoạn [0;2]?
Chọn D vì:
ĐKXĐ:D=[0 ; 4]
\(\begin{array}{l} \text { Ta có } \forall x \in[0 ; 4]: \\ 0 \leq 4 x-x^{2}=4-(x-2)^{2} \leq 4 \\ \text { Suy ra } 0 \leq k(x) \leq 2 \\ k(x)=0 \Leftrightarrow x=0 \text { hoặc } x=4 \\ k(x)=2 \Leftrightarrow x=2 \end{array}\)
Vậy k(x) có tập giá trị là đoạn [0;2]
Hàm số nào sau đây đồng biến trên khoảng (-1;1) ?
Chọn D vì xét hàm số \(y=-x^{3}+3 x\) ta có
TXĐ: \(D=\mathbb{R}\)
\(\begin{array}{l} \forall x_{1}, x_{2} \in \mathbb{R}, x_{1} \neq x_{2} \\ \frac{y\left(x_{2}\right)-y\left(x_{1}\right)}{x_{2}-x_{1}}=\frac{x_{1}^{3}-x_{2}^{3}+3\left(x_{2}-x_{1}\right)}{x_{2}-x_{1}} \\ =3-\left(x_{1}^{2}+x_{1} x_{2}+x_{2}^{2}\right) \\ \text { Với }\left|x_{1}\right|<1,\left|x_{2}\right|<1 \text { ta có } \\ x_{1}^{2}<1, x_{2}^{2}<1,\left|x_{1} x_{2}\right|<1 \Rightarrow x_{1} x_{2}<1 \\ \text { do đó } x_{1}^{2}+x_{1} x_{2}+x_{2}^{2}<3\Rightarrow 3-x_{1}^{2}+x_{1} x_{2}+x_{2}^{2}>0 \end{array}\)
Vậy hàm số đồng biến trên khoảng (-1;1)
Hàm số \(y=\frac{5-3 x}{5-3 m}\) (m là tham số) nghịch biến trên \(\mathbb{R}\) khi và chỉ khi
Ta có \(y = \frac{{5 - 3x}}{{5 - 3m}} = \frac{{ - 3x}}{{5 - 3m}} + \frac{5}{{5 - 3m}}\)
Hàm số nghịch biến khi và chỉ khi
\(\frac{-3}{5-3 m}<0 \Leftrightarrow 5-3 m>0 \Leftrightarrow m<\frac{5}{3}\)

