Cho ba điểm A, B, C tùy ý. Mệnh đề nào dưới đây đúng?

Cho đoạn thẳng AB có I là trung điểm. Mệnh đề nào dưới đây sai?

Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình \(\frac{x-2}{x+m}=\frac{x}{x-1}\) vô nghiệm. Tổng tất cả các phần tử của S bằng

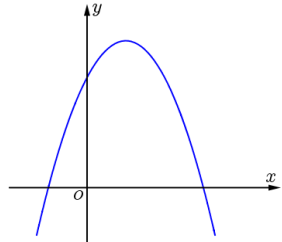
Cho hàm số \(y=a x^{2}-b x+c(a \neq 0)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng

Trong mặt phẳng Oxy , cho tam giác ABC có G là trọng tâm của tam giác, biết rằng\(A(1 ; 1), B(1 ;-2), G(2 ; 3)\) tọa độ của điểm C là:

Cho parabol \(y=a x^{2}+b x+3\) có  đỉnh \(I(2 ;-2)\) Khi đó giá trị a+2b bằng

Cho hai tập hợp A = (- 20 ; 20) và \(B=[2 m-4 ; 2 m+2)\) ( m là tham số). Có tất cả bao nhiêu giá trị nguyên của tham số m để \(A \cup B=A ?\)

Cho tam giác ABC cân tại A ,\(\widehat{B A C}=120^{\circ} \text { và } A B=a\). Tính \(\overrightarrow{B A} \cdot\overrightarrow{C A}\)

Cho \(A(2 ; 5), B(1 ; 3), C(5 ;-1)\). Tìm tọa độ điểm K sao cho \(\overrightarrow{A K}=3 \overrightarrow{B C}+2 \overrightarrow{C K}\)

Cho hai điểm \(A(-3,2), B(4,3)\) Điểm C thuộc trục Ox và có hoành độ dương để tam giác CAB vuông tại C . Khi đó tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành?

Cho hàm số \(y=f(x)=\left\{\begin{array}{lll} x-1 & \text { vói } & x \geq 1 \\ x^{2}+2 & \text { vói } & x<1 \end{array}\right.\). Tính\(f(-2)+f(2)\)

Cho điểm \(A(1 ;-2) ; B(1 ; 1) ; C(-1 ;-1)\)thành lập thành tam giác. Khi đó góc \(\widehat{A B C}\) bằng

Tìm tất cả các giá trị của m để hàm số \(y=\left(m^{4}-1\right) x+2020\) là hàm số bậc nhất?

Cho hàm số bậc hai \(y=a x^{2}-b x+c\) có đồ thị là (P). Biết rằng (P) có tọa độ đỉnh I (1;1988) và đi qua điểm M (3;2020). Khi đó, a+b+c bằng?

Cho tam giác ABC , điểm M thỏa mãn:\(2\overrightarrow{M A}-3 \overrightarrow{M B}=\overrightarrow{0}\). Khi đó, với điểm I bất kỳ, thỏa mãn\(\overrightarrow{I A}=m \overrightarrow{I M}+n \overrightarrow{I B}\) thì cặp số (m; n) bằng