Gọi AM là trung tuyến của tam giác ABC, và I là trung điểm của AM. Đẳng thức nào sau đây là đúng?
A. \(-\overrightarrow{I A}+\overrightarrow{I B}+\overrightarrow{I C}=\overrightarrow{0}\)
B. \(\overrightarrow{I A}+\overrightarrow{I B}+\overrightarrow{I C}=\overrightarrow{0}\)
C. \(2 \overrightarrow{I A}+\overrightarrow{I B}+\overrightarrow{IC}=\overrightarrow{0}\)
D. \(\overrightarrow{I A}+\overrightarrow{I B}-\overrightarrow{I C}=\overrightarrow{0}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Chọn C vì:
\(\begin{aligned} &2 \overrightarrow{I A}+\overrightarrow{I B}+\overrightarrow{I C}\\ &=2 \cdot \overrightarrow{I A}+2 \overrightarrow{I M}\\ &=2(\overrightarrow{I A}+\overrightarrow{IM})=2 \cdot \overrightarrow{0}=\overrightarrow{0} \end{aligned}\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số \(y=x^{2}-2 x+3\) . Tìm mệnh đề đúng trong các mệnh đề sau :
Tung độ giao điểm của đồ thị hàm số \(y=2 x^{2}+6 x+3\) và đường thẳng \(y=-2x-3\) là
Cho parabol \(y=a x^{2}-4 x+c\) đi qua điểm M(3;0) và có trục đối xứng x=2. Khi đó hệ số a, c là:
Parabol (P) đi qua ba điểm A(-1;0), B(0;-4) và C(1;-6) có phương trình là
Tập xác định của hàm số \(f(x) = \left\{ \begin{array}{l} \frac{x}{{x + 1}} \text{ nếu } x>0 \\ \frac{{\sqrt[3]{{x + 1}}}}{{x - 1}}\text{ nếu } -1\le x\le0 \end{array} \right.\)
Cho hai tập hợp \(B=\mathbb{R} \backslash(0 ;+\infty)\).Khi đó tập hợp B là
Cho parabol (P) \(y=3 x^{2}-2 x+1\) . Điểm nào sau đây là đỉnh của (P)
Cho tam giác đều ABC có cạnh bằng a. Giá trị \(|\overrightarrow{A B}-\vec{CA}|\) bằng bao nhiêu ?
Cho A(-2;-1), B(-1;3), C(m+1;n-2). Nếu \(2 \overrightarrow{A B}-3 \overrightarrow{A C}=\overrightarrow{0}\) thì ta có hệ thức nào sau đây đúng ?
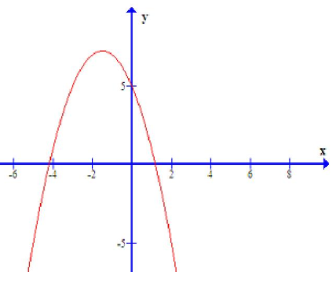
Parabol \(y=a x^{2}+b x+c\) có đồ thị như hình vẽ bên thì dấu của các hệ số a, b, c là:
Cho hình vuông ABCD có cạnh bằng a. Khi đó giá trị \(|\overrightarrow{A C}+\overrightarrow{B D}|\) bằng bao nhiêu ?
Cho A(2;1), B(1;2). Để tứ giác OABC là hình bình hành thì tọa độ điểm C là
Tập xác định của hàm số \(y=\frac{x^{2}-2 x+7}{x-1}\) là
Cho hình thang ABCD với hai cạnh đáy là AB=3a và CD=6a. Khi đó \(|\overrightarrow{AB}+\overrightarrow{C D}|\) bằng bao nhiêu ?

