Trong không gian với hệ tọa độ $Oxyz$, phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm $M\left( {2;3;3} \right),{\rm{ }}N\left( {2; - 1; - 1} \right),{\rm{ }}P\left( { - 2; - 1;3} \right)$ và có tâm thuộc mặt phẳng \((\alpha ):2x + 3y - z + 2 = 0\).
A.
\({x^2} + {y^2} + {z^2} - 2x + 2y - 2z - 10 = 0\)
B.
\({x^2} + {y^2} + {z^2} - 4x + 2y - 6z - 2 = 0\)
C.
\({x^2} + {y^2} + {z^2} + 4x - 2y + 6z + 2 = 0\)
D.
\({x^2} + {y^2} + {z^2} - 2x + 2y - 2z - 2 = 0\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
- Liệt kê các phương trình mặt cầu cho trong 4 đáp án
+ A cho mặt cầu tâm \({I_A}(1, - 1,1)\) và \({R_A} = \sqrt {13} \)
+ B cho mặt cầu tâm \({I_B}(2, - 1,3)\) và \({R_B} = 4\)
+ C cho mặt cầu tâm \({I_C}( - 2,1, - 3)\) và \({R_C} = 2\sqrt 3 \)
+ D cho mặt cầu tâm \({I_D}(1, - 1,1)\) và \({R_D} = \sqrt 5 \)
- Kiểm tra các tâm có thuộc mặt phẳng \((\alpha )\) hay không. Loại được đáp án C.
- Ta thấy\({I_A} \equiv {I_D} = I(1, - 1,1)\), nên ta tính bán kính $R = IM$ rồi so sánh với \({R_A},{R_D}\) .
Có \(IM = \sqrt {{1^2} + {4^2} + {2^2}} = \sqrt {21} \) . Ta thấy \(IM \ne {R_A} \ne {R_D}\). Loại A và D
Hướng dẫn giải:
Xét từng đáp án:
- Xác định tâm mặt cầu và thay vào mặt phẳng.
- Tính bán kính mặt cầu và kiểm tra khoảng cách từ tâm đến các điểm \(A,B,C\) bằng bán kính.
Giải thích thêm:
Tự luận:
\(\overrightarrow {MN} = \left( {0; - 4; - 4} \right)\), \(\overrightarrow {NP} = \left( { - 4;0;4} \right)\)
Gọi (P) và (Q) lần lượt là mặt phẳng trung trực của MN và NP.
Khi đó tâm I của mặt cầu thuộc (P) và (Q)
Ta có:
(P) qua trung điểm A(2;1;1) của MN và nhận vecto \(\overrightarrow {{n_1}} = \left( {0;1;1} \right)\) làm vecto pháp tuyến nên có phương trình:
\(y - 1 + z - 1 = 0 \Leftrightarrow y + z - 2 = 0\)
(Q) qua trung điểm B(0;-1;1) của NP và nhận vecto \(\overrightarrow {{n_2}} = \left( {1;0; - 1} \right)\) làm vecto pháp tuyến nên có phương trình:
\(x - 0 - \left( {z - 1} \right) = 0 \Leftrightarrow x - z + 1 = 0\)
Do I là tâm mặt cầu đi qua 3 điểm M,N,P nên I phải thuộc mặt phẳng trung trực của MN và NP.
Khi đó tọa độ của I là nghiệm của hệ
\(\left\{ \begin{array}{l}2x + 3y - z + 2 = 0\\y + z - 2 = 0\\x - z + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 1\\z = 3\end{array} \right.\)
=> I(2;-1;3)
=> R=4
Mặt cầu cần tìm là:
\({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = 16\)
\( \Leftrightarrow {x^2} + {y^2} + {z^2} - 4x + 2y - 6z - 2 = 0\)
- Liệt kê các phương trình mặt cầu cho trong 4 đáp án
+ A cho mặt cầu tâm \({I_A}(1, - 1,1)\) và \({R_A} = \sqrt {13} \)
+ B cho mặt cầu tâm \({I_B}(2, - 1,3)\) và \({R_B} = 4\)
+ C cho mặt cầu tâm \({I_C}( - 2,1, - 3)\) và \({R_C} = 2\sqrt 3 \)
+ D cho mặt cầu tâm \({I_D}(1, - 1,1)\) và \({R_D} = \sqrt 5 \)
- Kiểm tra các tâm có thuộc mặt phẳng \((\alpha )\) hay không. Loại được đáp án C.
- Ta thấy\({I_A} \equiv {I_D} = I(1, - 1,1)\), nên ta tính bán kính $R = IM$ rồi so sánh với \({R_A},{R_D}\) .
Có \(IM = \sqrt {{1^2} + {4^2} + {2^2}} = \sqrt {21} \) . Ta thấy \(IM \ne {R_A} \ne {R_D}\). Loại A và D
Hướng dẫn giải:
Xét từng đáp án:
- Xác định tâm mặt cầu và thay vào mặt phẳng.
- Tính bán kính mặt cầu và kiểm tra khoảng cách từ tâm đến các điểm \(A,B,C\) bằng bán kính.
Giải thích thêm:
Tự luận:
\(\overrightarrow {MN} = \left( {0; - 4; - 4} \right)\), \(\overrightarrow {NP} = \left( { - 4;0;4} \right)\)
Gọi (P) và (Q) lần lượt là mặt phẳng trung trực của MN và NP.
Khi đó tâm I của mặt cầu thuộc (P) và (Q)
Ta có:
(P) qua trung điểm A(2;1;1) của MN và nhận vecto \(\overrightarrow {{n_1}} = \left( {0;1;1} \right)\) làm vecto pháp tuyến nên có phương trình:
\(y - 1 + z - 1 = 0 \Leftrightarrow y + z - 2 = 0\)
(Q) qua trung điểm B(0;-1;1) của NP và nhận vecto \(\overrightarrow {{n_2}} = \left( {1;0; - 1} \right)\) làm vecto pháp tuyến nên có phương trình:
\(x - 0 - \left( {z - 1} \right) = 0 \Leftrightarrow x - z + 1 = 0\)
Do I là tâm mặt cầu đi qua 3 điểm M,N,P nên I phải thuộc mặt phẳng trung trực của MN và NP.
Khi đó tọa độ của I là nghiệm của hệ
\(\left\{ \begin{array}{l}2x + 3y - z + 2 = 0\\y + z - 2 = 0\\x - z + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 1\\z = 3\end{array} \right.\)
=> I(2;-1;3)
=> R=4
Mặt cầu cần tìm là:
\({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = 16\)
\( \Leftrightarrow {x^2} + {y^2} + {z^2} - 4x + 2y - 6z - 2 = 0\)
CÂU HỎI CÙNG CHỦ ĐỀ
Trong không gian với hệ tọa độ $Oxyz,$ cho điểm $M\left( {1;1;2} \right).$ Hỏi có bao nhiêu mặt phẳng $\left( P \right)$ đi qua $M$ và cắt các trục $x'Ox,\,\,y'Oy,\,\,z'Oz$ lần lượt tại các điểm $A,\,\,B,\,\,C$ sao cho $OA = OB = OC \ne 0\,\,?$
Họ nguyên hàm của hàm số \(f\left( x \right)={{x}^{3}}+2x\) là:
Hình chiếu của điểm \(M\left( {2;2; - 1} \right)\) lên mặt phẳng \(\left( {Oyz} \right)\) là:
Trong không gian Oxyz, cho ba mặt phẳng \(\left( P \right):\,\,x+y-3z+1=0;\,\,\left( Q \right):\,\,2x+3y+z-1=0\); \(\left( R \right):\,\,x+2y+4z-2=0\). Xét mặt phẳng (T) chứa giao tuyến của hai mặt phẳng (P) và (Q), có $\overrightarrow {{n_{\left( T \right)}}} = \left( {1;a;b} \right)$ và tạo với mặt phẳng (R) một góc \(\alpha \). Biết \(\cos \alpha =\dfrac{23}{\sqrt{679}}\) có phương trình:
Nếu đặt $\left\{ \begin{array}{l}u = \ln \left( {x + 2} \right)\\{\rm{d}}v = x\,{\rm{d}}x\end{array} \right.$ thì tích phân $I = \int\limits_0^1 {x.\ln \left( {x + 2} \right){\rm{d}}x} $ trở thành
Trong không gian Oxyz, cho điểm A(1;2;3). Hình chiếu vuông góc của điểm A trên mặt phẳng (Oxy) là điểm
Cho véc tơ \(\overrightarrow u = \left( {x;y;z} \right)\) và một số thực \(k \ne 0\). Tọa độ véc tơ \(\dfrac{1}{k}.\overrightarrow u \) là:
Tìm nguyên hàm của hàm số \(f\left( x \right)=\sin 2x.\)
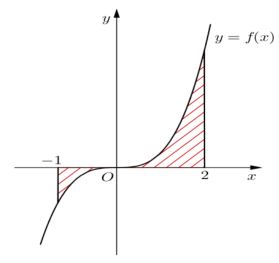
Gọi \(S\) là diện tích hình phẳng \(\left( H \right)\) giới hạn bởi các đường $y=f\left( x \right),~$trục hoành và hai đường thẳng \(x = - 1,x = 2\) (như hình vẽ). Đặt $a=\underset{-1}{\overset{0}{\mathop \int }}\,f\left( x \right)dx,~b=\underset{0}{\overset{2}{\mathop \int }}\,f\left( x \right)dx.$ Mệnh đề nào sau đây đúng?
Cho hàm số $f\left( x \right)$ thỏa mãn $f'\left( x \right){\left[ {f\left( x \right)} \right]^{2018}} = x.{e^x}{\mkern 1mu} {\mkern 1mu} \forall x \in R$ và $f\left( 1 \right) = 1$. Hỏi phương trình $f\left( x \right) = - \dfrac{1}{e}$ có bao nhiêu nghiệm?
Cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\), khi đó độ dài đoạn thẳng \(AB\) được tính theo công thức:
Tìm nguyên hàm của hàm số \(f(x) = \dfrac{{{x^3}}}{{\sqrt {4 - {x^2}} }}\).
Một viên gạch hoa hình vuông cạnh \(40\)cm. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng

Nếu \(\int\limits_{ - 2}^0 {\left( {4 - {e^{ -{\frac{x}{2}}}}} \right)dx} = K - 2e\) thì giá trị của \(K\) là

