Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
- Khối đa diện đều loại \(\left\{ {n;p} \right\}\):
+ \(n\) là số cạnh của mỗi mặt.
+ \(p\) là số cạnh cùng đi qua một đỉnh.
Vì số đỉnh mỗi mặt bằng số cạnh mỗi mặt nên \(n\) cũng số đỉnh mỗi mặt.
Giải thích thêm:
Với một số em không nhớ kĩ định nghĩa \(n,p\) thì sẽ chọn nhầm đáp án D là sai.
- Khối đa diện đều loại \(\left\{ {n;p} \right\}\):
+ \(n\) là số cạnh của mỗi mặt.
+ \(p\) là số cạnh cùng đi qua một đỉnh.
Vì số đỉnh mỗi mặt bằng số cạnh mỗi mặt nên \(n\) cũng số đỉnh mỗi mặt.
Giải thích thêm:
Với một số em không nhớ kĩ định nghĩa \(n,p\) thì sẽ chọn nhầm đáp án D là sai.
CÂU HỎI CÙNG CHỦ ĐỀ
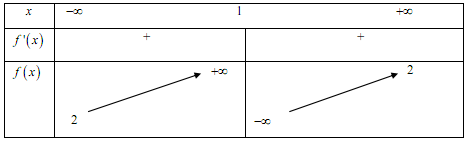
Giá trị lớn nhất của hàm số $y = x - \dfrac{1}{x}$ trên $\left( { - \infty ; - 1} \right]$ là:
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
Hai hình chóp tam giác đều có chung đáy là tam giác đều và đỉnh thuộc hai phía khác nhau so với mặt đáy. Hai hình này bằng nhau khi:
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
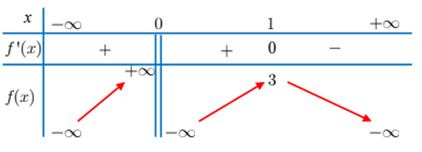
Với các giá trị thực của tham số \(m\), phương trình \(f\left( x \right)=m\) có nhiều nhất bao nhiêu nghiệm?
Khối đa diện lồi có \(8\) đỉnh và \(6\) mặt thì có số cạnh là:
Tìm tất cả các giá trị của $m$ để hàm số $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$ có cực đại và cực tiểu.
Cho điểm $I\left( {0;4} \right)$ và đường cong $\left( C \right):y = - {x^2} + 3x$. Phương trình $\left( C \right)$ đối với hệ tọa độ $\left( {IXY} \right)$ là:
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ như hình vẽ bên
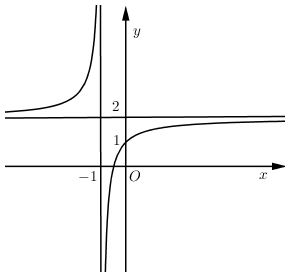
Chọn khẳng định đúng:
Cho lăng trụ đều \(ABC.A'B'C'\), cạnh đáy bằng a, góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính thể tích khối lăng trụ đó.
Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{x - 1}}{{ - 3x + 2}}\) là?
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:
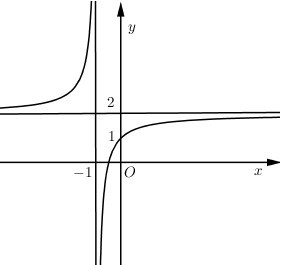
Chọn kết luận đúng:
Vật thể nào trong các vật thể sau không phải là khối đa diện?

Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$

