Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
Ta có: ${\log _{\frac{1}{{\sqrt 3 }}}}81 = {\log _{{{\sqrt 3 }^{ - 1}}}}{3^4} = - {\log _{\sqrt 3 }}{3^4} $
$= - {\log _{{3^{\frac{1}{2}}}}}{3^4} = - \dfrac{1}{{1/2}}{\log _3}{3^4} = - 2{\log _3}{3^4} = - 2.4 = - 8$
Hướng dẫn giải:
Sủ dụng các công thức ${\log _{{a^n}}}b = \dfrac{1}{n}{\log _a}b$ và ${\log _a}{b^n} = n{\log _a}b$.
Giải thích thêm:
Một số em sẽ giải sai như sau: ${\log _{\frac{1}{{\sqrt 3 }}}}81 = {\log _{{3^{\frac{1}{2}}}}}{3^4} = \dfrac{1}{2}.4 = 2$ và chọn đáp án A là sai.
Hs có thể sử dụng luôn công thức \({\log _{{a^n}}}{b^m} = \dfrac{m}{n}{\log _a}b\) để tìm đáp án.
Ta có: ${\log _{\frac{1}{{\sqrt 3 }}}}81 = {\log _{{{\sqrt 3 }^{ - 1}}}}{3^4} = - {\log _{\sqrt 3 }}{3^4} $
$= - {\log _{{3^{\frac{1}{2}}}}}{3^4} = - \dfrac{1}{{1/2}}{\log _3}{3^4} = - 2{\log _3}{3^4} = - 2.4 = - 8$
Hướng dẫn giải:
Sủ dụng các công thức ${\log _{{a^n}}}b = \dfrac{1}{n}{\log _a}b$ và ${\log _a}{b^n} = n{\log _a}b$.
Giải thích thêm:
Một số em sẽ giải sai như sau: ${\log _{\frac{1}{{\sqrt 3 }}}}81 = {\log _{{3^{\frac{1}{2}}}}}{3^4} = \dfrac{1}{2}.4 = 2$ và chọn đáp án A là sai.
Hs có thể sử dụng luôn công thức \({\log _{{a^n}}}{b^m} = \dfrac{m}{n}{\log _a}b\) để tìm đáp án.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho mặt cầu \(S\left( {I;R} \right)\) và mặt phẳng \(\left( P \right)\) cách I một khoảng bằng \(\frac{R}{2}\). Khi đó giao của \(\left( P \right)\) và \(\left( S \right)\) là đường tròn có chu vi bằng:
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
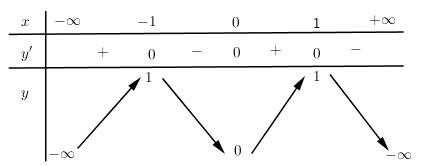
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Cho mặt cầu \(\left( S \right)\) và mặt phẳng \(\left( P \right)\) cắt nhau tại nhiều hơn một điểm. Giao tuyến của chúng là:
Tâm đối xứng của đồ thị hàm số bậc ba có hoành độ là nghiệm của phương trình
Cho hàm số \(y = f\left( x \right)\) đồng biến và có đạo hàm trên \(\left( { - 5;5} \right)\). Khi đó:
Tính thể tích \(V\) của khối trụ ngoại tiếp hình lập phương có cạnh bằng $a$.
Cho một mặt cầu bán kính bằng $1$. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Cho hàm số $y = - {x^3} + 3m{x^2} - 3m - 1$ với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng $d:x + 8y - 74 = 0$.
Một người gửi vào ngân hàng số tiền $A$ đồng, lãi suất $r\% $ mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kì hạn $3$ tháng. Công thức tính số tiền cả vốn lẫn lãi mà người đó có sau $2$ năm là:
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
Công thức tính thể tích khối nón biết diện tích đáy \({S_d}\) và đường sinh \(l\) là: