Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
Ta có $y' = - 3{x^2} + 6mx = - 3x\left( {x - 2m} \right);{\rm{ }}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2m\end{array} \right.$.
Để đồ thị hàm số có hai điểm cực trị \( \Leftrightarrow m \ne 0\).
Khi đó gọi $A\left( {0; - 3m - 1} \right)$ và $B\left( {2m;4{m^3} - 3m - 1} \right)$ là hai điểm cực trị của đồ thị hàm số.
Suy ra trung điểm của $AB$ là điểm $I\left( {m;2{m^3} - 3m - 1} \right)$và\(\overrightarrow {AB} = \left( {2m;4{m^3}} \right) = 2m\left( {1;2{m^2}} \right)\).
Đường thẳng \(d\) có một vectơ chỉ phương là \(\overrightarrow u = \left( {8; - 1} \right).\)
Ycbt \( \Leftrightarrow \left\{ \begin{array}{l}I \in d\\\overrightarrow {AB} .\overrightarrow u = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m + 8\left( {2{m^3} - 3m - 1} \right) - 74 = 0\\8 - 2{m^2} = 0\end{array} \right. \Leftrightarrow m = 2.\)
Hướng dẫn giải:
- Tính \(y'\) và tìm hai nghiệm \({x_1},{x_2}\) của phương trình \(y' = 0\)
- Tìm tọa độ các điểm cực trị.
- Sử dụng điều kiện đối xứng tìm \(m\).
Giải thích thêm:
Cách trắc nghiệm:
Đáp án A: Với \(m = 1\) thì \(y = - {x^3} + 3{x^2} - 4\)
Có \(y' = - 3{x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y\left( 0 \right) = - 4\\x = 2 \Rightarrow y\left( 2 \right) = 0\end{array} \right.\)
Do đó hai điểm cực trị của đồ thị hàm số là \(A\left( {0; - 4} \right)\) và \(B\left( {2;0} \right)\).
Trung điểm của \(AB\) là \(I\left( {1; - 2} \right)\).
Dễ thấy \(I \notin d\) vì \(1 + 8.\left( { - 2} \right) - 74 \ne 0\) nên hai điểm cực trị không đối xưng qua đường thẳng \(d\).
Loại A.
Tương tự với các đáp án còn lại, chú ý cũng có thể kiểm tra \(\overrightarrow {AB} \) vuông góc với \(\overrightarrow {{u_d}} \) để loại nghiệm.
Ta có $y' = - 3{x^2} + 6mx = - 3x\left( {x - 2m} \right);{\rm{ }}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2m\end{array} \right.$.
Để đồ thị hàm số có hai điểm cực trị \( \Leftrightarrow m \ne 0\).
Khi đó gọi $A\left( {0; - 3m - 1} \right)$ và $B\left( {2m;4{m^3} - 3m - 1} \right)$ là hai điểm cực trị của đồ thị hàm số.
Suy ra trung điểm của $AB$ là điểm $I\left( {m;2{m^3} - 3m - 1} \right)$và\(\overrightarrow {AB} = \left( {2m;4{m^3}} \right) = 2m\left( {1;2{m^2}} \right)\).
Đường thẳng \(d\) có một vectơ chỉ phương là \(\overrightarrow u = \left( {8; - 1} \right).\)
Ycbt \( \Leftrightarrow \left\{ \begin{array}{l}I \in d\\\overrightarrow {AB} .\overrightarrow u = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m + 8\left( {2{m^3} - 3m - 1} \right) - 74 = 0\\8 - 2{m^2} = 0\end{array} \right. \Leftrightarrow m = 2.\)
Hướng dẫn giải:
- Tính \(y'\) và tìm hai nghiệm \({x_1},{x_2}\) của phương trình \(y' = 0\)
- Tìm tọa độ các điểm cực trị.
- Sử dụng điều kiện đối xứng tìm \(m\).
Giải thích thêm:
Cách trắc nghiệm:
Đáp án A: Với \(m = 1\) thì \(y = - {x^3} + 3{x^2} - 4\)
Có \(y' = - 3{x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y\left( 0 \right) = - 4\\x = 2 \Rightarrow y\left( 2 \right) = 0\end{array} \right.\)
Do đó hai điểm cực trị của đồ thị hàm số là \(A\left( {0; - 4} \right)\) và \(B\left( {2;0} \right)\).
Trung điểm của \(AB\) là \(I\left( {1; - 2} \right)\).
Dễ thấy \(I \notin d\) vì \(1 + 8.\left( { - 2} \right) - 74 \ne 0\) nên hai điểm cực trị không đối xưng qua đường thẳng \(d\).
Loại A.
Tương tự với các đáp án còn lại, chú ý cũng có thể kiểm tra \(\overrightarrow {AB} \) vuông góc với \(\overrightarrow {{u_d}} \) để loại nghiệm.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho mặt cầu \(S\left( {I;R} \right)\) và mặt phẳng \(\left( P \right)\) cách I một khoảng bằng \(\frac{R}{2}\). Khi đó giao của \(\left( P \right)\) và \(\left( S \right)\) là đường tròn có chu vi bằng:
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
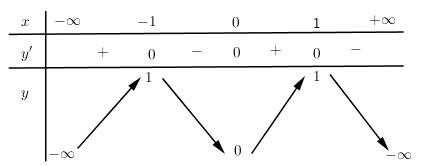
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Cho mặt cầu \(\left( S \right)\) và mặt phẳng \(\left( P \right)\) cắt nhau tại nhiều hơn một điểm. Giao tuyến của chúng là:
Tâm đối xứng của đồ thị hàm số bậc ba có hoành độ là nghiệm của phương trình
Cho hàm số \(y = f\left( x \right)\) đồng biến và có đạo hàm trên \(\left( { - 5;5} \right)\). Khi đó:
Tính thể tích \(V\) của khối trụ ngoại tiếp hình lập phương có cạnh bằng $a$.
Cho một mặt cầu bán kính bằng $1$. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Một người gửi vào ngân hàng số tiền $A$ đồng, lãi suất $r\% $ mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kì hạn $3$ tháng. Công thức tính số tiền cả vốn lẫn lãi mà người đó có sau $2$ năm là:
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
Công thức tính thể tích khối nón biết diện tích đáy \({S_d}\) và đường sinh \(l\) là: