Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA \bot \left( {ABC} \right)\) và \(SA = a\). Tính thể tích khối chóp \(S.ABC\).
A.
\({V_{S.ABC}} = \dfrac{{{a^3}\sqrt 3 }}{6}\)
B.
\({V_{S.ABC}} = \dfrac{{{a^3}\sqrt 3 }}{4}\)
C.
\({V_{S.ABC}} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)
D.
\({V_{S.ABC}} = \dfrac{{{a^3}\sqrt 3 }}{3}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
Ta có \(SA = a,{\rm{ }}{{\rm{S}}_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\). Suy ra thể tích \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\).
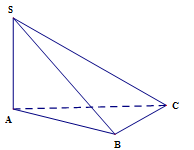
Hướng dẫn giải:
- Tính diện tích đáy $ABC$
- Tính thể tích theo công thức $V=\dfrac{1}{3}S.h$
Ta có \(SA = a,{\rm{ }}{{\rm{S}}_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\). Suy ra thể tích \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\).

Hướng dẫn giải:
- Tính diện tích đáy $ABC$
- Tính thể tích theo công thức $V=\dfrac{1}{3}S.h$
CÂU HỎI CÙNG CHỦ ĐỀ
Giá trị lớn nhất của hàm số $y = x - \dfrac{1}{x}$ trên $\left( { - \infty ; - 1} \right]$ là:
Hai hình chóp tam giác đều có chung đáy là tam giác đều và đỉnh thuộc hai phía khác nhau so với mặt đáy. Hai hình này bằng nhau khi:
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
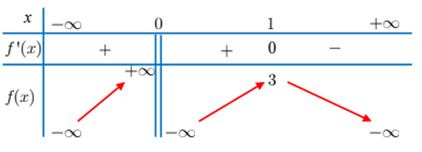
Với các giá trị thực của tham số \(m\), phương trình \(f\left( x \right)=m\) có nhiều nhất bao nhiêu nghiệm?
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
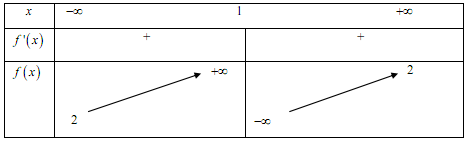
Khối đa diện lồi có \(8\) đỉnh và \(6\) mặt thì có số cạnh là:
Tìm tất cả các giá trị của $m$ để hàm số $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$ có cực đại và cực tiểu.
Cho điểm $I\left( {0;4} \right)$ và đường cong $\left( C \right):y = - {x^2} + 3x$. Phương trình $\left( C \right)$ đối với hệ tọa độ $\left( {IXY} \right)$ là:
Cho lăng trụ đều \(ABC.A'B'C'\), cạnh đáy bằng a, góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính thể tích khối lăng trụ đó.
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ như hình vẽ bên
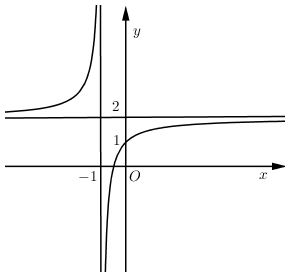
Chọn khẳng định đúng:
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:
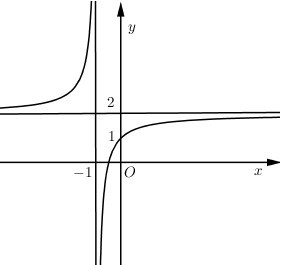
Chọn kết luận đúng:
Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{x - 1}}{{ - 3x + 2}}\) là?
Vật thể nào trong các vật thể sau không phải là khối đa diện?

Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$

