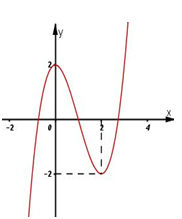
Cho hàm số \(y = {x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4\,\,\,\left( {{C_m}} \right)\). Giá trị của tham số \(m\) để đường thẳng \(\left( d \right):y = x + 4\) cắt \(\left( {{C_m}} \right)\) tại ba điểm phân biệt \(A\left( {0;4} \right),\,\,B,\,\,C\) sao cho tam giác \(KBC\) có diện tích bằng \(8\sqrt 2 \) với điểm \(K\left( {1;3} \right)\) là:
A.
\(m = \frac{{1 - \sqrt {137} }}{2}\)
B.
\(m = \frac{{1 + \sqrt {137} }}{2}\)
C.
\(m = \frac{{1 \pm \sqrt {137} }}{2}\)
D.
\(m = \frac{{ \pm 1 + \sqrt {137} }}{2}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
+ Xét phương trình hoành độ giao điểm của đồ thị và đường thẳng ta có:
\(\begin{array}{l}{x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4 = x + 4\\ \Leftrightarrow {x^3} + 2m{x^2} + \left( {m + 2} \right)x = 0\\ \Leftrightarrow x\left( {{x^2} + 2mx + m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} + 2mx + m + 2 = 0\,\,\,\,\,\left( 1 \right)\end{array} \right.\end{array}\)
Để \(\left( d \right)\) cắt \(\left( {{C_m}} \right)\) tại 3 điểm phân biệt thì phương trình \(\left( 1 \right)\) có 2 nghiệm phân biệt khác 0
\( \Rightarrow \left\{ \begin{array}{l}\Delta ; > 0\\0 + 2m.0 + m + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - m - 2 > 0\\m \ne - 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 1\end{array} \right.\\m \ne 2\end{array} \right.\) .
Gọi \({x_1};\,\,{x_2}\) là \(2\) nghiệm phân biệt của phương trình \(\left( 1 \right)\) \( \Rightarrow B\left( {{x_1};{x_1} + 4} \right);\,\,\,C\left( {{x_2};{x_2} + 4} \right).\)
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2m\\{x_1}.{x_2} = m + 2\end{array} \right..\)
Ta có: \({S_{KBC}} = \frac{1}{2}.d\left( {K,BC} \right).BC.\)
Phương trình đường thẳng \(\left( d \right):\,\,y = x + 4 \Leftrightarrow x - y + 4 = 0\).
Vì \(B,\,\,C\) thuộc đường thẳng \(\left( d \right)\) nên ta có: \(d\left( {K,BC} \right) = d\left( {K;d} \right) = \frac{{\left| {1 - 3 + 4} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 .\)
\(\begin{array}{l}BC = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{x_2} + 4 - {x_1} - 4} \right)}^2}} \\BC = \sqrt {2{{\left( {{x_1} - {x_2}} \right)}^2}} \\BC = \sqrt 2 .\sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \\BC = \sqrt 2 .\sqrt {4{m^2} - 4\left( {m + 2} \right)} \\BC = 2\sqrt 2 .\sqrt {{m^2} - m - 2} \end{array}\)
Theo bài ra ta có:
\(\begin{array}{l}{S_{KBC}} = 8\sqrt 2 \\ \Leftrightarrow \frac{1}{2}.\sqrt 2 .2\sqrt 2 \sqrt {{m^2} - m - 2} = 8\sqrt 2 \\ \Leftrightarrow \sqrt {{m^2} - m - 2} = 4\sqrt 2 \\ \Leftrightarrow {m^2} - m - 2 = 32\\ \Leftrightarrow {m^2} - m - 34 = 0\\ \Leftrightarrow m = \frac{{1 \pm \sqrt {137} }}{2}\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(m = \frac{{1 \pm \sqrt {137} }}{2}\).
Hướng dẫn giải:
+ Xét phương trình hoành độ giao điểm và tìm mối quan hệ giữa \({x_1},{x_2}\) là hoành độ của \(B,C\).
+ Viết công thức tính diện tích tam giác \(KBC\) và tìm \(m\).
+ Xét phương trình hoành độ giao điểm của đồ thị và đường thẳng ta có:
\(\begin{array}{l}{x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4 = x + 4\\ \Leftrightarrow {x^3} + 2m{x^2} + \left( {m + 2} \right)x = 0\\ \Leftrightarrow x\left( {{x^2} + 2mx + m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} + 2mx + m + 2 = 0\,\,\,\,\,\left( 1 \right)\end{array} \right.\end{array}\)
Để \(\left( d \right)\) cắt \(\left( {{C_m}} \right)\) tại 3 điểm phân biệt thì phương trình \(\left( 1 \right)\) có 2 nghiệm phân biệt khác 0
\( \Rightarrow \left\{ \begin{array}{l}\Delta ; > 0\\0 + 2m.0 + m + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - m - 2 > 0\\m \ne - 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 1\end{array} \right.\\m \ne 2\end{array} \right.\) .
Gọi \({x_1};\,\,{x_2}\) là \(2\) nghiệm phân biệt của phương trình \(\left( 1 \right)\) \( \Rightarrow B\left( {{x_1};{x_1} + 4} \right);\,\,\,C\left( {{x_2};{x_2} + 4} \right).\)
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2m\\{x_1}.{x_2} = m + 2\end{array} \right..\)
Ta có: \({S_{KBC}} = \frac{1}{2}.d\left( {K,BC} \right).BC.\)
Phương trình đường thẳng \(\left( d \right):\,\,y = x + 4 \Leftrightarrow x - y + 4 = 0\).
Vì \(B,\,\,C\) thuộc đường thẳng \(\left( d \right)\) nên ta có: \(d\left( {K,BC} \right) = d\left( {K;d} \right) = \frac{{\left| {1 - 3 + 4} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 .\)
\(\begin{array}{l}BC = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{x_2} + 4 - {x_1} - 4} \right)}^2}} \\BC = \sqrt {2{{\left( {{x_1} - {x_2}} \right)}^2}} \\BC = \sqrt 2 .\sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \\BC = \sqrt 2 .\sqrt {4{m^2} - 4\left( {m + 2} \right)} \\BC = 2\sqrt 2 .\sqrt {{m^2} - m - 2} \end{array}\)
Theo bài ra ta có:
\(\begin{array}{l}{S_{KBC}} = 8\sqrt 2 \\ \Leftrightarrow \frac{1}{2}.\sqrt 2 .2\sqrt 2 \sqrt {{m^2} - m - 2} = 8\sqrt 2 \\ \Leftrightarrow \sqrt {{m^2} - m - 2} = 4\sqrt 2 \\ \Leftrightarrow {m^2} - m - 2 = 32\\ \Leftrightarrow {m^2} - m - 34 = 0\\ \Leftrightarrow m = \frac{{1 \pm \sqrt {137} }}{2}\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(m = \frac{{1 \pm \sqrt {137} }}{2}\).
Hướng dẫn giải:
+ Xét phương trình hoành độ giao điểm và tìm mối quan hệ giữa \({x_1},{x_2}\) là hoành độ của \(B,C\).
+ Viết công thức tính diện tích tam giác \(KBC\) và tìm \(m\).
CÂU HỎI CÙNG CHỦ ĐỀ
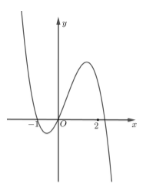
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(R\). Nếu hàm số \(f\left( x \right)\) nghịch biến trên \(R\) thì:
Giá trị lớn nhất của hàm số $f\left( x \right) = \dfrac{{\sin x}}{x}$ trên đoạn $\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$ là:
Cho hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có bảng biến thiên:
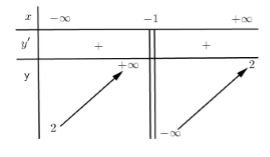
Giá trị của \(2{c^2} - 5{d^2}\) bằng
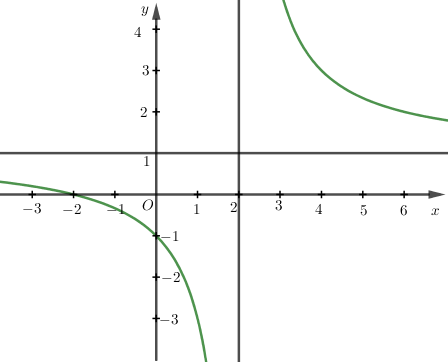
Đường cong ở hình bên là đồ thị hàm số \(y=\dfrac{ax+2}{cx+b}\) với \(a,b,c\) là các số thực. Mệnh đề nào sau đây đúng?
Hàm số \(y = - {x^3} + {x^2} + 1\,\) xác định khi:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = 1,\,\,\forall x \in \mathbb{R}\). Mệnh đề nào sau đây đúng?
Tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^3}}}{3} - 2{x^2} + x + 2$ song song với đường thẳng $y = - 2x + 5$ có phương trình là:
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
Cho hai số thực \(x,\,y\) thỏa mãn \({x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} = \sqrt {6 + 4x - {x^2}} \). Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(T = \left| {\sqrt {{x^2} + {y^2}} - a} \right|\). Có bao nhiêu giá trị nguyên thuộc đoạn \(\left[ { - 10;\,10} \right]\) của tham số \(a\) để \(M \ge 2m\)?
Biết rằng hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a\not = 0} \right)\) có đồ thị là một trong các dạng dưới đây:
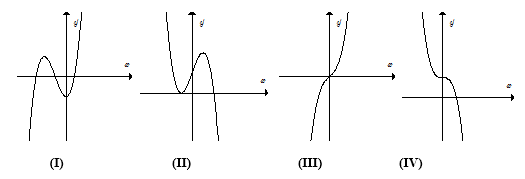
Mệnh đề nào sau đây là đúng?
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
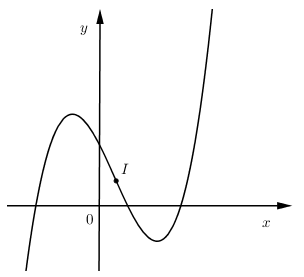
Cho hàm số y = f (x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?