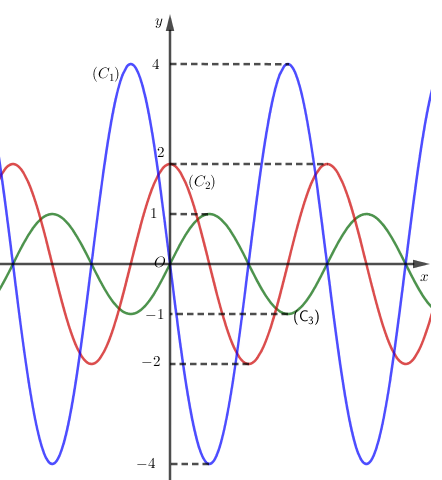
Cho hàm số $y = f(x)$ có đạo hàm cấp một $f'(x)$ và đạo hàm cấp hai $f''(x)$ trên $\mathbb{R}$. Biết đồ thị hàm số $y = f(x),{\mkern 1mu} {\mkern 1mu} y = f'(x),{\mkern 1mu} y = f''(x)$ là một trong các đường cong $({C_1}),({C_2}),({C_3})$ ở hình vẽ bên. Hỏi đồ thị hàm số $y = f(x),{\mkern 1mu} {\mkern 1mu} y = f'(x),{\mkern 1mu} y = f''(x)$ lần lượt theo thứ tự nào dưới đây?
A.
$({C_2}),({C_1}),({C_3}).$
B.
$({C_1}),({C_2}),({C_3})$
C.
$({C_3}),({C_1}),({C_2})$
D.
$({C_3}),({C_2}),({C_1})$
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
Quan sát dáng đồ thị các hàm số ta thấy đều có dạng đường hình \(\sin \) nên ta dự đoán các hàm số ở đây có thể là dạng \(y = \sin ax\) hoặc \(y = \cos ax\)
Thấy rằng hai đồ thị \(\left( {{C_1}} \right),\left( {{C_3}} \right)\) đi qua điểm \(O\left( {0;0} \right)\) nên một trong hai đồ thị hàm số \(\left( {{C_1}} \right),\left( {{C_3}} \right)\) sẽ là của hàm \(y = f\left( x \right) = \sin ax\), đồ thị \(\left( {{C_2}} \right)\) là của \(y = f'\left( x \right)\) nên loại A và C.
Ta xét hàm số \(y = f\left( x \right) = \sin ax\) có \(f'\left( x \right) = a.\cos ax,f''\left( x \right) = - {a^2}\sin ax\)
Dễ thấy \(f'\left( 0 \right) = a > 0\).
Quan sát các giá trị trên đồ thị ta dễ dàng nhận ra \(a = 2\).
Vậy ta có các hàm số \(y = \sin 2x,y = 2\cos 2x,y = - 4\sin 2x\) lần lượt có đồ thị là \(\left( {{C_3}} \right),\left( {{C_2}} \right),\left( {{C_1}} \right)\)
Vậy \(\left( {{C_3}} \right),\left( {{C_2}} \right),\left( {{C_1}} \right)\) là đồ thị hàm số \(y = f\left( x \right),y = f'\left( x \right),y = f''\left( x \right)\)
Hướng dẫn giải:
Dùng phương pháp chọn điểm rơi, đặc biệt hóa. Chọn một hàm số đã biết có dạng đồ thị như hình vẽ và tính các đạo hàm \(f',f''\) rồi đối chiếu dạng đồ thị bài cho.
Quan sát dáng đồ thị các hàm số ta thấy đều có dạng đường hình \(\sin \) nên ta dự đoán các hàm số ở đây có thể là dạng \(y = \sin ax\) hoặc \(y = \cos ax\)
Thấy rằng hai đồ thị \(\left( {{C_1}} \right),\left( {{C_3}} \right)\) đi qua điểm \(O\left( {0;0} \right)\) nên một trong hai đồ thị hàm số \(\left( {{C_1}} \right),\left( {{C_3}} \right)\) sẽ là của hàm \(y = f\left( x \right) = \sin ax\), đồ thị \(\left( {{C_2}} \right)\) là của \(y = f'\left( x \right)\) nên loại A và C.
Ta xét hàm số \(y = f\left( x \right) = \sin ax\) có \(f'\left( x \right) = a.\cos ax,f''\left( x \right) = - {a^2}\sin ax\)
Dễ thấy \(f'\left( 0 \right) = a > 0\).
Quan sát các giá trị trên đồ thị ta dễ dàng nhận ra \(a = 2\).
Vậy ta có các hàm số \(y = \sin 2x,y = 2\cos 2x,y = - 4\sin 2x\) lần lượt có đồ thị là \(\left( {{C_3}} \right),\left( {{C_2}} \right),\left( {{C_1}} \right)\)
Vậy \(\left( {{C_3}} \right),\left( {{C_2}} \right),\left( {{C_1}} \right)\) là đồ thị hàm số \(y = f\left( x \right),y = f'\left( x \right),y = f''\left( x \right)\)
Hướng dẫn giải:
Dùng phương pháp chọn điểm rơi, đặc biệt hóa. Chọn một hàm số đã biết có dạng đồ thị như hình vẽ và tính các đạo hàm \(f',f''\) rồi đối chiếu dạng đồ thị bài cho.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho mặt cầu \(S\left( {I;R} \right)\) và mặt phẳng \(\left( P \right)\) cách I một khoảng bằng \(\frac{R}{2}\). Khi đó giao của \(\left( P \right)\) và \(\left( S \right)\) là đường tròn có chu vi bằng:
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
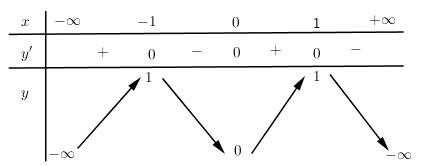
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Cho mặt cầu \(\left( S \right)\) và mặt phẳng \(\left( P \right)\) cắt nhau tại nhiều hơn một điểm. Giao tuyến của chúng là:
Tâm đối xứng của đồ thị hàm số bậc ba có hoành độ là nghiệm của phương trình
Tính thể tích \(V\) của khối trụ ngoại tiếp hình lập phương có cạnh bằng $a$.
Cho hàm số \(y = f\left( x \right)\) đồng biến và có đạo hàm trên \(\left( { - 5;5} \right)\). Khi đó:
Cho một mặt cầu bán kính bằng $1$. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?
Cho hàm số $y = - {x^3} + 3m{x^2} - 3m - 1$ với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng $d:x + 8y - 74 = 0$.
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Một người gửi vào ngân hàng số tiền $A$ đồng, lãi suất $r\% $ mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kì hạn $3$ tháng. Công thức tính số tiền cả vốn lẫn lãi mà người đó có sau $2$ năm là:
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
Công thức tính thể tích khối nón biết diện tích đáy \({S_d}\) và đường sinh \(l\) là: