Viết các số đo diện tích dưới dạng số thập phân

1. Ôn tập bảng đơn vị đo diện tích

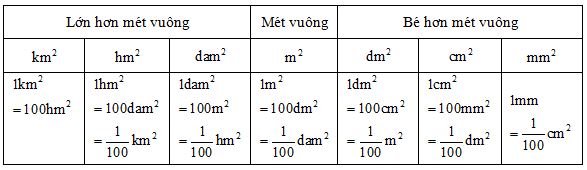
Nhận xét: Trong bảng đơn vị đo diện tích, hai đơn vị đo liền nhau hơn (kém) nhau \(100\) lần, tức là:

- Đơn vị lớn gấp \(100\) lần đơn vị bé;

- Đơn vị bé bằng \(\dfrac{1}{{100}}\) đơn vị lớn.

Lưu ý: Quan hệ giữa một số đơn vị đo diện tích thông dụng:

\(\begin{array}{l}1k{m^2} = 1000000{m^2} &  & 1k{m^2} = 100ha\\1ha = 10000{m^2} &  &  & 1{m^2} = 100d{m^2} = 10000c{m^2}\end{array}\)

2. Cách viết các số đo diện tích dưới dạng số thập phân

Phương pháp chung:

- Xác định hai đơn vị đo diện tích đã cho là gì và tìm được mối liên hệ giữa chúng.

- Viết số đo đã cho thành phân số thập phân hoặc hỗn số có phần phân số là phân số thập phân.

- Viết phân số hoặc hỗn số vừa tìm được thành số thập phân gọn nhất.

Ví dụ 1: Viết số thập phân thích hợp vào chỗ chấm: \(8{m^2}\,9d{m^2} = ...{m^2}\).

Phương pháp:

- Xác định hai đơn vị đo khối lượng đã cho (\({m^2}\) và \(d{m^2}\)) và tìm mối liên hệ giữa chúng: \(1{m^2} = 100d{m^2}\) hay \(1d{m^2} = \dfrac{1}{{100}}{m^2}\).

- Đổi số đo diện tích đã cho thành hỗn số có phần phân số là phân số thập phân

- Đổi hỗn số vừa tìm được thành số thập phân gọn nhất.

Cách giải:

Theo bảng đơn vị đo diện tích ta có \(1{m^2} = 100d{m^2}\) hay \(1d{m^2} = \dfrac{1}{{100}}{m^2}\).

Nên \(8{m^2}\,9d{m^2} = 8\dfrac{9}{{100}}{m^2} = 8,09{m^2}\)

Vậy \(8{m^2}\,9d{m^2} = 8,09{m^2}\).

Ví dụ 2: Viết số thập phân thích hợp vào chỗ chấm: \(85{m^2}\,\, = ...ha\).

Cách giải:

Theo bảng đơn vị đo diện tích ta có \(1ha = 1h{m^2} = 10000{m^2}\) hay \(1{m^2} = \dfrac{1}{{10000}}ha\).

Nên \(85{m^2}\,\, = \dfrac{{85}}{{10000}}ha = 0,0085ha\)

Vậy \(85{m^2}\,\, = 0,0085ha\).

Ví dụ 3: Viết số thập phân thích hợp vào chỗ chấm: \(1357c{m^2} = ...d{m^2}\).

Phương pháp:

- Xác định hai đơn vị đo diện tích đã cho (\(c{m^2}\) và \(d{m^2}\)) và tìm mối liên hệ giữa chúng: \(1d{m^2} = 100c{m^2}\) hay \(1c{m^2} = \dfrac{1}{{100}}d{m^2}\).

- Đổi \(1357c{m^2} = 1300c{m^2} + 57c{m^2}\), sau đó đổi \(1300c{m^2}\) sang đơn vị \(d{m^2}\) rồi làm tiếp tương tự như những ví dụ bên trên.

Cách giải:

\(1357c{m^2} = 1300c{m^2} + 57c{m^2} = 13d{m^2} + 57c{m^2} = 13d{m^2}\,57c{m^2} = 13\dfrac{{57}}{{100}}d{m^2} = 13,57d{m^2}\)

Vậy \(1357c{m^2} = 13,57d{m^2}\).

Ví dụ 4: Viết số thích hợp vào chỗ chấm:  \(23,6k{m^2} = ...k{m^2}\,...ha = ...ha\).

Phương pháp:

- Xác định hai đơn vị đo diện tích đã cho là \(k{m^2}\) và \(ha\) và tìm  mối liên hệ giữa chúng \(1k{m^2} = 100ha\) hay \(1ha = \dfrac{1}{{100}}k{m^2}\).

- Viết \(23,6k{m^2}\) dưới dạng hỗn số có phần phân số là phân số thập phân.

- Tách hỗn số thành phần nguyên và phần phân số, hai thành phần đều có đơn vị là \(k{m^2}.\)

- Chuyển phần phân số với đơn vị là \(k{m^2}\) sang đơn vị \(ha\).

Cách giải:

$23,6k{m^2} = 23\dfrac{6}{{10}}k{m^2} = \,23\dfrac{{60}}{{100}}k{m^2} = 23k{m^2} + \dfrac{{60}}{{100}}k{m^2} = 23k{m^2}\,60ha = 2300ha + 60ha = 2360ha$Vậy \(23,6k{m^2} = 23k{m^2}\,60ha = 2360ha\).