Ôn tập về giải toán

1. Tìm hai số khi biết tổng và hiệu của hai số đó

Phương pháp giải:

Bước 1: Vẽ sơ đồ

Bước 2: Tìm số bé và số lớn theo công thức:

Bước 3: Kết luận (hay đáp số)

Ví dụ: Tổng hai số là $71$ và hiệu hai số đó là $13$. Tìm hai số đó.

Cách giải:

Ta có sơ đồ:

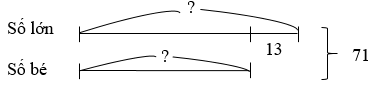
Số lớn là:         $(71 + 13):\,2 = 42$

Số bé là:          $71 - 42 = 29$

                                    Đáp số: số bé: $29$;  số lớn: $42$.

2. Tỉ số

Định nghĩa: Tỉ số của hai số $a$ và $b$ là $a:b$ hay $\dfrac{a}{b}$ ($b$ khác $0$)

Ví dụ: tỉ số của hai số $3$ và $5$ là $\dfrac{3}{5}$.

Lưu ý: Muốn lập tỉ số của hai đơn vị đo đại lượng thì chúng phải cùng đơn vị đo.

Ví dụ: Tìm tỉ số của hai đoạn thẳng có độ dài là $1dm$ và $12cm.$

Cách giải:

Đổi $1dm = 10cm$

Tỉ số của hai đoạn thẳng trên là: $\dfrac{{10}}{{12}} = \dfrac{5}{6}$.

3. Tìm hai số khi biết tổng và tỉ số của hai số đó

Phương pháp giải:

Bước 1: Vẽ sơ đồ.

Bước 2: Tìm tổng số phần bằng nhau.

Bước 3: Tìm giá trị một phần  (lấy tổng ban đầu chia tổng số phần bằng nhau).

Bước 4: Tìm hai số theo công thức:

             Số bé = Giá trị một phần × số phần của số bé

hoặc

             Số lớn =  Giá trị một phần × số phần của số lớn

Bước 5: Kết luận (hay đáp số).

Ví dụ: Cho hai số có tổng là $63$. Tìm hai số đó, biết rằng tỉ số của hai số là $\dfrac{4}{5}$.

Cách giải

Ta có sơ đồ:

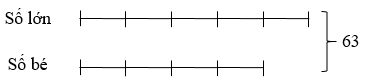
Theo sơ đồ, tổng số phần bằng nhau là:

            $4 + 5 = 9$ (phần)

Giá trị một phần là:

            $63:9 = 7$

Số bé là:

            $7 \times 4 = 28$

Số lớn là:

            $63 - 28 = 35$

                        Đáp số:  số bé: $28$;  số lớn: $35$.

4. Tìm hai số khi biết hiệu và tỉ số của hai số đó

Phương pháp giải:

Bước 1: Vẽ sơ đồ.

Bước 2: Tìm hiệu số phần bằng nhau.

Bước 3: Tìm giá trị một phần (lấy hiệu ban đầu chia hiệu số phần bằng nhau).

Bước 4: Tìm hai số theo công thức:

            Số bé = Giá trị một phần × số phần của số bé

hoặc

           Số lớn =  Giá trị một phần × số phần của số lớn

Bước 5: Kết luận (hay đáp số)

Ví dụ: Tìm hai số khi biết hiệu của hai số là $52$ và tỉ số của hai số đó là $\dfrac{3}{7}$.

Cách giải

Ta có sơ đồ:

Theo sơ đồ, hiệu số phần bằng nhau là:

            $7 - 3 = 4$ (phần)

Giá trị một phần là:

            $52:4 = 13$

Số lớn là:

            $13 \times 7 = 91$

Số bé là:

            $91 - 52 = 39$

                        Đáp số:  số bé: $39$;  số lớn: $91$.