Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm \(M\left( {2;1;1} \right)\), cắt và vuông góc với đường thẳng \(\Delta :\dfrac{{x - 2}}{{ - 2}} = \dfrac{{y - 8}}{1} = \dfrac{z}{1}\). Tìm tọa độ giao điểm của d và mặt phẳng \(\left( {Oyz} \right)\).

Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm  \(A(0;2; - 1)\) , \(B(2;0;1)\). Tìm tọa độ điểm $M$ nằm trên trục $Ox$ sao cho :\(M{A^2} + M{B^2}\) đạt giá trị bé nhất.

Trong không gian tọa độ \(Oxyz\), tính thể tích khối tứ diện \(OBCD\) biết \(B\left( {2;0;0} \right),C\left( {0;1;0} \right),D\left( {0;0; - 3} \right)\).

Công thức tính độ dài véc tơ \(\overrightarrow u  = \left( {a;b;c} \right)\) là:

Để tính $I = \int\limits_0^{\dfrac{\pi }{2}} {{x^2}\,\cos x\,{\rm{d}}x} $ theo phương pháp tích phân từng phần, ta đặt

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} - 2{\rm{x}} - 4y + 4{\rm{z}} - 16 = 0$ và đường thẳng $d:\dfrac{{x - 1}}{1} = \dfrac{{y + 3}}{2} = \dfrac{z}{2}$. Mặt phẳng nào trong các mặt phẳng sau chứa $d$ và tiếp xúc với mặt cầu $(S)$.

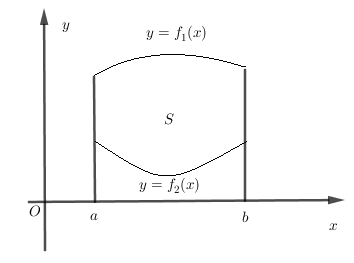
Cho hai hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và có đồ thị như hình vẽ bên. Gọi $S$ là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng \(x = a,x = b\). Thể tích $V$ của vật thể tròn xoay tạo thành khi quay $S$ quanh trục $Ox$ được tính bởi công thức nào sau đây ? 

Hàm số \(F\left( x \right) = {x^5} + 5{x^3} - x + 2\) là một nguyên hàm của hàm số nào sau đây? (C là hằng số).

Trên mặt phẳng tọa độ \(Oxy\), tìm tập hợp các điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện \(\left| {z - 2} \right| + \left| {z + 2} \right| = 10\).

Gọi \(A\) là điểm biểu diễn của số phức \(z = 3 + 2i\) và \(B\) là điểm biểu diễn của số phức \(z' = 2 + 3i\). Mệnh đề nào sau đây là đúng?

Cho $I = \int\limits_0^1 {\left( {2x - {m^2}} \right)dx} $. Có bao nhiêu giá trị nguyên dương m để $I + 3 \ge 0$?

Tính tích phân \(I=\int\limits_{0}^{3}{\frac{\text{d}x}{x+2}}\). 

Trong không gian Oxyz, phương trình mặt phẳng đi qua ba điểm \(A\left( { - 3;0;0} \right);\,\,B\left( {0; - 2;0} \right);\) \(C\left( {0;0;1} \right)\) được viết dưới dạng \(ax + by - 6z + c = 0\). Giá trị của \(T = a + b - c\) là :

Cho hàm số \(y = f\left( x \right)\) liên tục và nhận giá trị dương trên \(\mathbb{R}.\) Gọi \({D_1}\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\) các đường \(x = 0,\,\,x = 1\) và trục \(Ox.\) Gọi \({D_2}\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = \dfrac{1}{3}f\left( x \right),\) các đường \(x = 0,\,\,\,x = 1\) và trục \(Ox.\) Quay các hình phẳng \({D_1},\,\,{D_2}\) quanh trục \(Ox\) ta được các khối tròn xoay có thể tích lần lượt là \({V_1},\,\,{V_2}.\)

Khẳng định nào sau đâu là đúng?

Trong không gian \(Oxyz,\) cho mặt cầu \((S):{(x - 1)^2} + {(y - 2)^2} + {(z + 1)^2} = 6,\) tiếp xúc với hai mặt phẳng \((P):x + y + 2z\, + \,5 = 0,\,\,(Q):2x - y + z\, - \,5 = 0\) lần lượt tại các tiếp điểm $A,\,\,B.$ Độ dài đoạn thẳng $AB$ là

Cho các phát biểu sau: (Với $C$ là hằng số):

(I) \(\int\limits_{}^{} {0dx}  = x + C\)

(II) \(\int\limits_{}^{} {\dfrac{1}{x}dx}  = \ln \left| x \right| + C\)

(III) \(\int\limits_{}^{} {\sin xdx}  =  - \cos x + C\)

(IV) \(\int\limits_{}^{} {\cot xdx}  =  - \dfrac{1}{{{{\sin }^2}x}} + C\)

(V) \(\int\limits_{}^{} {{e^x}dx}  = {e^x} + C\)

(VI) \(\int\limits_{}^{} {{x^n}dx}  = \dfrac{{{x^{n + 1}}}}{{n + 1}} + C\,\,\left( {\forall n \ne  - 1} \right)\)

Số phát biểu đúng là: