Đáy của hình chóp $S.ABCD$ là một hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt đáy và có độ dài là \(a\). Thể tích khối tứ diện \(S.BCD\) bằng:
A.
\(\dfrac{{{a^3}}}{6}\)
B.
\(\dfrac{{{a^3}}}{3}\)
C.
\(\dfrac{{{a^3}}}{4}\)
D.
\(\dfrac{{{a^3}}}{8}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
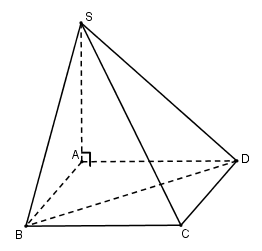
Ta có: \({S_{\Delta BCD}} = \dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{2}{a^2}\)
\({V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}}}{6}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \({S_{\Delta BCD}}\)
- Bước 2: Tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án B vì không đọc kí đề, coi \(ABCD\) đáy và tính diện tích đáy \(S = {a^2}\) là sai.
Cách làm khác: Các em có thể nhận xét \({V_{S.BCD}} = \dfrac{1}{2}{V_{S.ABCD}}\) nên có thể tính \({V_{S.ABCD}}\) rồi suy ra đáp án.

Ta có: \({S_{\Delta BCD}} = \dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{2}{a^2}\)
\({V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}}}{6}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \({S_{\Delta BCD}}\)
- Bước 2: Tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án B vì không đọc kí đề, coi \(ABCD\) đáy và tính diện tích đáy \(S = {a^2}\) là sai.
Cách làm khác: Các em có thể nhận xét \({V_{S.BCD}} = \dfrac{1}{2}{V_{S.ABCD}}\) nên có thể tính \({V_{S.ABCD}}\) rồi suy ra đáp án.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân tại $A$. \(AB = AC = 2a,\widehat {CAB} = {120^0}.\) Mặt phẳng \(\left( {AB'C'} \right)\) tạo với đáy một góc \({60^0}\). Thể tích khối lăng trụ là:
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
Cho hình chóp \(S.ABC\) có đáy \(ABC\) vuông tại \(A\) và \(SB\) vuông góc với đáy. Biết \(SB = a,SC\) hợp với \(\left( {SAB} \right)\) một góc \({30^0}\) và \(\left( {SAC} \right)\) hợp với đáy \(\left( {ABC} \right)\) một góc \({60^0}\). Thể tích khối chóp là:
Trong một hình đa diện lồi, mỗi cạnh là cạnh chung của tất cả bao nhiêu mặt?
Trong các hình dưới đây, hình nào là khối đa diện?
Cho tứ diện \(ABCD\) có \(AB,\,\,AC,\,\,AD\) đôi một vuông góc và \(AB = 2a,\,\,\,AC = 3a,\,\,AD = 4a.\) Thể tích của khối tứ diện đó là:
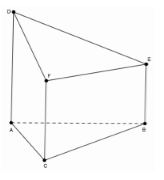
Cho đa diện \(ABCDEF\) có \(AD,BE,CF\) đôi một song song. \(AD \bot \left( {ABC} \right)\), \(AD + BE + CF = 5\), diện tích tam giác \(ABC\) bằng \(10\). Thể tích đa diện \(ABCDEF\) bằng
Khối đa diện lồi có \(8\) đỉnh và \(6\) mặt thì có số cạnh là:
Cho hình chóp đều $S.ABCD$ có diện tích đáy là \(16c{m^2}\), diện tích một mặt bên là \(8\sqrt 3 c{m^2}\). Thể tích khối chóp $S.ABCD$ là:
Có bao nhiêu cách chọn ra ba đỉnh từ các đỉnh của một hình lập phương để thu được một tam giác đều ?