Cho hình trụ $(T)$ có $\left( C \right),\,\,\left( {C'} \right)$ là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn $(C)$ và hình vuông ngoại tiếp của $(C)$ có một hình chữ nhật kích thước $1 \times 2$ (như hình vẽ dưới đây). Thể tích của khối trụ $(T)$ là
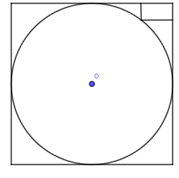
A.
$250\pi $.
B.
$100\pi $.
C.
$\dfrac{{100\pi }}{3}$.
D.
$\dfrac{{250\pi }}{3}$.
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
Gắn hệ trục tọa độ trong mặt phẳng chứa đường tròn $(C)$ như hình vẽ.
Phương trình đường tròn $(C):$ ${\left( {x - R} \right)^2} + {\left( {y - R} \right)^2} = {R^2},\,\,\,(R > 2)$
Điểm $\left( {1;2} \right)$ thuộc (C)$ \Rightarrow {\left( {1 - R} \right)^2} + {\left( {2 - R} \right)^2} = {R^2} \Leftrightarrow {R^2} - 6R + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}R = 1\,\,(L)\\R = 5\end{array} \right. \Leftrightarrow R = 5$
$ \Rightarrow $ Chiều cao của khối trụ $h = 2R = 10$
Thể tích khối trụ là: $V = \pi {R^2}h = \pi {.5^2}.10 = 250\pi $.
Hướng dẫn giải:
- Gắn hệ trục tọa độ trong mặt phẳng chứa đường tròn $(C)$, tìm bán kính của đường tròn $\left( C \right)$.
- Tính thể tích khối trụ.
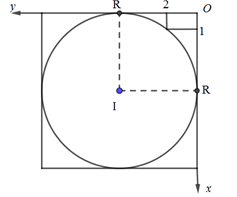
Gắn hệ trục tọa độ trong mặt phẳng chứa đường tròn $(C)$ như hình vẽ.
Phương trình đường tròn $(C):$ ${\left( {x - R} \right)^2} + {\left( {y - R} \right)^2} = {R^2},\,\,\,(R > 2)$
Điểm $\left( {1;2} \right)$ thuộc (C)$ \Rightarrow {\left( {1 - R} \right)^2} + {\left( {2 - R} \right)^2} = {R^2} \Leftrightarrow {R^2} - 6R + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}R = 1\,\,(L)\\R = 5\end{array} \right. \Leftrightarrow R = 5$
$ \Rightarrow $ Chiều cao của khối trụ $h = 2R = 10$
Thể tích khối trụ là: $V = \pi {R^2}h = \pi {.5^2}.10 = 250\pi $.
Hướng dẫn giải:
- Gắn hệ trục tọa độ trong mặt phẳng chứa đường tròn $(C)$, tìm bán kính của đường tròn $\left( C \right)$.
- Tính thể tích khối trụ.

CÂU HỎI CÙNG CHỦ ĐỀ
Một khối trụ có bán kính đáy bằng \(2\), chiều cao bằng \(3\). Tính thể tích \(V\) của khối trụ.
Mặt cầu đi qua các đỉnh của một hình đa diện thì nó được gọi là:
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng $10 cm$. Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?

Cho khối cầu có đường kính bằng 12. Thể tích khối cầu đã cho bằng
Khi quay hình chữ nhật \(MNPQ\) quanh đường thẳng \(AB\) với \(A,B\) lần lượt là trung điểm của \(MN,PQ\) ta được một hình trụ có đường kính đáy:
Hình lập phương có độ dài cạnh \(a = 6\) thì đường kính mặt cầu ngoại tiếp là:
Số mặt phẳng tiếp diện của mặt cầu tại một điểm thuộc mặt cầu là:
Công thức tính thể tích khối nón biết diện tích đáy \({S_d}\) và đường sinh \(l\) là:
Cho hình nón có bán kính đáy \(r = \sqrt 3 ,\) độ dài đường sinh \(l = 4.\) Tính diện tích xung quanh của hình nón đó?
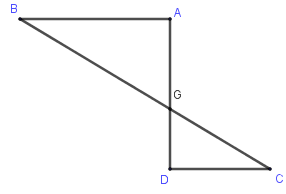
Số hình nón có được khi quay hình sau quanh trục \(BC\) là:
Đề thi THPT QG - 2021 - mã 102
Cho khối trụ có bán kính đáy \(r = 4\) và chiều cao \(h = 3\). Thể tích của khối trụ đã cho bằng
Cho mặt cầu \(\left( S \right)\) cố định và điểm \(A\) di nguyển trong không gian, vị trí của \(A\) để tập hợp các tiếp điểm của tiếp tuyến với mặt cầu kẻ từ \(A\) là đường tròn lớn là:
Tính diện tích toàn phần của hình trụ có đường cao bằng 2 và đường kính đáy bằng 8.
Cho mặt cầu \(\left( S \right)\) tâm \(O\) và các điểm \(A\), \(B\), \(C\) nằm trên mặt cầu \(\left( S \right)\) sao cho \(AB = 3\), \(AC = 4\), \(BC = 5\) và khoảng cách từ \(O\) đến mặt phẳng \(\left( {ABC} \right)\) bằng \(1\). Thể tích của khối cầu \(\left( S \right)\) bằng
Cho tam giác \(ABC\) vuông cân tại \(A\), \(AB = a\). Cho tam giác \(ABC\) quay xung quanh cạnh \(AC\) ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.

