Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
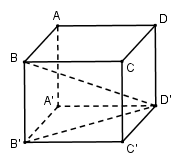
Vì $A'B'C'D'$ là hình vuông cạnh $a$ nên \(B'D' = a\sqrt 2 \)
\(BB' \bot \left( {A'B'C'D'} \right) \Rightarrow BB' \bot B'D' \Rightarrow \Delta BB'D'\) vuông tại \(B' \Rightarrow BB' = \sqrt {BD{'^2} - B'D{'^2}} = \sqrt {6{a^2} - 2{a^2}} = 2a\)
Vậy \({V_{ABCD.A'B'C'D'}} = BB'.{S_{ABCD}} = 2a.{a^2} = 2{a^3}\)
Hướng dẫn giải:
- Tính diện tích đáy \({S_{A'B'C'D'}}\) và độ dài đường cao \(BB'\).
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\).

Vì $A'B'C'D'$ là hình vuông cạnh $a$ nên \(B'D' = a\sqrt 2 \)
\(BB' \bot \left( {A'B'C'D'} \right) \Rightarrow BB' \bot B'D' \Rightarrow \Delta BB'D'\) vuông tại \(B' \Rightarrow BB' = \sqrt {BD{'^2} - B'D{'^2}} = \sqrt {6{a^2} - 2{a^2}} = 2a\)
Vậy \({V_{ABCD.A'B'C'D'}} = BB'.{S_{ABCD}} = 2a.{a^2} = 2{a^3}\)
Hướng dẫn giải:
- Tính diện tích đáy \({S_{A'B'C'D'}}\) và độ dài đường cao \(BB'\).
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\).
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình chóp tứ giác đều $S.ABCD$ có chiều cao $h$, góc ở đỉnh của mặt bên bằng \({60^0}\). Thể tích hình chóp là:
Đề thi THPT QG - 2021 - mã 101
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 2a,\) góc giữa hai mặt phẳng \(\left( {A'B{\rm{D}}} \right)\) và \(\left( {ABCD} \right)\) bằng \({30^0}\). Thể tích của khối hộp chữ nhật đã cho bằng
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Đường thẳng \(SC\) tạo với đáy góc \({45^0}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Thể tích của khối chóp \(S.MCDN\) là:
Cho đoạn thẳng \(AB\). Mặt phẳng \(\left( P \right)\) là mặt phẳng trung trực của \(AB\) thì:
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là \(6cm\) và \(8cm\), biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:
Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$, và \(A'A = A'B = A'C = a\sqrt {\dfrac{7}{{12}}} \) . Thể tích khối lăng trụ \(ABC.A'B'C'\) theo $a$ là:
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng \(4\) và tạo với đáy góc \({60^0}\). Thể tích của khối chóp đó là:
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\)
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là:
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất:

