Cho hình chóp \(S.ABC\), đáy là tam giác \(ABC\) có \(AB = BC\sqrt 5 \), \(AC = 2BC\sqrt 2 \), hình chiếu của \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(O\) của cạnh \(AC\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng 2. Mặt phẳng \(\left( {SBC} \right)\) hợp với mặt phẳng \(\left( {ABC} \right)\) một góc \(\alpha \) thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp \(S.ABC\) bằng \(\dfrac{{\sqrt a }}{b}\), trong đó \(a,\,\,b \in {\mathbb{N}^*}\), \(a\) là số nguyên tố. Tổng \(a + b\) bằng:
A.
\(6\)
B.
\(5\)
C.
\(7\)
D.
\(4\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
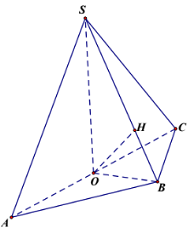
Gọi \(H\) là hình chiếu của \(O\) lên \(SB\).
Ta có: \(OB = \sqrt {\dfrac{{2B{C^2} + 2B{A^2} - A{C^2}}}{4}} = BC\), \(OC = \dfrac{1}{2}AC = BC\sqrt 2 \). Suy ra \(OB \bot BC\).
Dễ thấy \(\angle SBO = \alpha \) và \(OH = d\left( {O;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = 1\).
Suy ra \(SO = \dfrac{{OH}}{{\cos \alpha }} = \dfrac{1}{{\cos \alpha }}\), \(OB = \dfrac{{OH}}{{\sin \alpha }} = \dfrac{1}{{\sin \alpha }}\).
\( \Rightarrow BC = OB = \dfrac{1}{{\sin \alpha }}\).
Thể tích khối chóp \(S.ABC\) là:
\(\begin{array}{l}{V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}} = \dfrac{1}{3}SO.2{S_{OBC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{1}{{\cos \alpha }}.{\left( {\dfrac{1}{{\sin \alpha }}} \right)^2} = \dfrac{1}{{3\cos \alpha .{{\sin }^2}\alpha }}\end{array}\)
Áp dụng bất đẳng thức Cô-si ta có:
\(\begin{array}{l}1 = \dfrac{1}{2}{\sin ^2}\alpha + \dfrac{1}{2}{\sin ^2}\alpha + {\cos ^2}\alpha \ge 3.\sqrt[3]{{\dfrac{1}{4}{{\sin }^4}\alpha .{{\cos }^2}\alpha }}\\ \Leftrightarrow \dfrac{1}{{27}} \ge \dfrac{1}{4}.si{n^4}\alpha .co{s^2}\alpha \Rightarrow \dfrac{1}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} \ge \dfrac{{3\sqrt 3 }}{2}\\ \Rightarrow {V_{S.ABC}} \ge \dfrac{{\sqrt 3 }}{2}\end{array}\)
Vậy \(\min {V_{S.ABC}} = \dfrac{{\sqrt 3 }}{2}\). Dấu “=” xảy ra \( \Leftrightarrow {\cos ^2}\alpha = \dfrac{1}{2}{\sin ^2}\alpha = \dfrac{1}{3} \Leftrightarrow \cos \alpha = \dfrac{{\sqrt 3 }}{3}\).
\( \Rightarrow a = 3,\,\,b = 2\).
Vậy \(a + b = 3 + 2 = 5\).

Gọi \(H\) là hình chiếu của \(O\) lên \(SB\).
Ta có: \(OB = \sqrt {\dfrac{{2B{C^2} + 2B{A^2} - A{C^2}}}{4}} = BC\), \(OC = \dfrac{1}{2}AC = BC\sqrt 2 \). Suy ra \(OB \bot BC\).
Dễ thấy \(\angle SBO = \alpha \) và \(OH = d\left( {O;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = 1\).
Suy ra \(SO = \dfrac{{OH}}{{\cos \alpha }} = \dfrac{1}{{\cos \alpha }}\), \(OB = \dfrac{{OH}}{{\sin \alpha }} = \dfrac{1}{{\sin \alpha }}\).
\( \Rightarrow BC = OB = \dfrac{1}{{\sin \alpha }}\).
Thể tích khối chóp \(S.ABC\) là:
\(\begin{array}{l}{V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}} = \dfrac{1}{3}SO.2{S_{OBC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{1}{{\cos \alpha }}.{\left( {\dfrac{1}{{\sin \alpha }}} \right)^2} = \dfrac{1}{{3\cos \alpha .{{\sin }^2}\alpha }}\end{array}\)
Áp dụng bất đẳng thức Cô-si ta có:
\(\begin{array}{l}1 = \dfrac{1}{2}{\sin ^2}\alpha + \dfrac{1}{2}{\sin ^2}\alpha + {\cos ^2}\alpha \ge 3.\sqrt[3]{{\dfrac{1}{4}{{\sin }^4}\alpha .{{\cos }^2}\alpha }}\\ \Leftrightarrow \dfrac{1}{{27}} \ge \dfrac{1}{4}.si{n^4}\alpha .co{s^2}\alpha \Rightarrow \dfrac{1}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} \ge \dfrac{{3\sqrt 3 }}{2}\\ \Rightarrow {V_{S.ABC}} \ge \dfrac{{\sqrt 3 }}{2}\end{array}\)
Vậy \(\min {V_{S.ABC}} = \dfrac{{\sqrt 3 }}{2}\). Dấu “=” xảy ra \( \Leftrightarrow {\cos ^2}\alpha = \dfrac{1}{2}{\sin ^2}\alpha = \dfrac{1}{3} \Leftrightarrow \cos \alpha = \dfrac{{\sqrt 3 }}{3}\).
\( \Rightarrow a = 3,\,\,b = 2\).
Vậy \(a + b = 3 + 2 = 5\).
CÂU HỎI CÙNG CHỦ ĐỀ
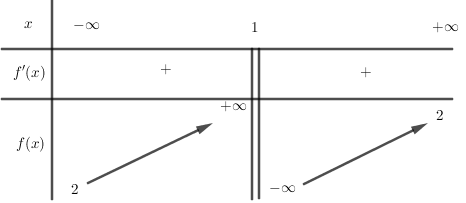
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai?
Cho hàm số $y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx.$ Tìm $m$ để đồ thị hàm số có hai điểm cực trị là $A, B$ sao cho đường thẳng $AB$ vuông góc với $d:\,x - y - 9 = 0$
Nếu $\log_a b{\rm{ }} = {\rm{ }}p$ thì $\log_a{a^2}{b^4}$ bằng:
Cho $n \in Z, n>0$, với điều kiện nào của $a$ thì đẳng thức sau xảy ra: ${a^{ - n}} = \dfrac{1}{{{a^n}}}$?
Với điều kiện các logarit đều có nghĩa, chọn mệnh đề đúng:
Cho các phát biểu sau:
(I). Nếu \(C = \sqrt {AB} \) thì \(2\ln C = \ln A + \ln B\) với $A, B$ là các biểu thức luôn nhận giá trị dương.
(II). \(\left( {a - 1} \right){\log _a}x \ge 0 \Leftrightarrow x \ge 1\) với \(a > 0,a \ne 1\)
(III). \({m^{{{\log }_a}m}} = {n^{{{\log }_a}n}},\) với \(m,n > 0\) và \(a > 0,a \ne 1\)
(IV).\(\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = - \infty \)
Số phát biểu đúng là
Biết đồ thị các hàm số $y = {x^3} + \dfrac{5}{4}x - 2$ và $y = {x^2} + x - 2$ tiếp xúc nhau tại điểm $M({x_0}\,;\,{y_0})$. Tìm ${x_0}.$
Chọn kết luận đúng: Đồ thị hàm số bậc bốn trùng phương
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?
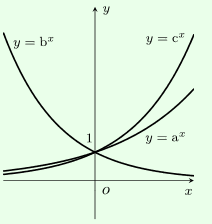
Cho các đồ thị hàm số \(y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c \ne 1} \right)\), chọn khẳng định đúng:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, \(AB = 4,SA = SB = SC = 12\). Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \(\dfrac{{BF}}{{BS}} = \dfrac{2}{3}\). Thể tích khối tứ diện \(MNEF\) bằng