Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
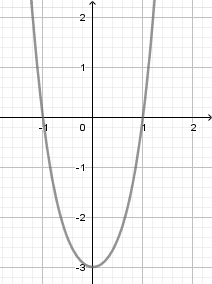
Từ dáng đồ thị ta có $a > 0$ nên loại A, C
Đồ thị hàm số có điểm cực tiểu là $\left( {0; - 3} \right).$
Do hàm số chỉ có một điểm cực trị nên $y' = 0$ phải có duy nhất một nghiệm ${x_0}$ và $y\left( {{x_0}} \right) = - 3.$
Kiểm tra ta chỉ thấy đáp án D là phù hợp.
Ngoài ra, đáp án B bị loại vì phương trình $y'=0$ ở đáp án B có $3$ nghiệm phân biệt.
Hướng dẫn giải:
Quan sát đồ thị hàm số và nhận xét dáng điệu đồ thị, điểm cực đại, cực tiểu, đối chiếu các đáp án đã cho.
Từ dáng đồ thị ta có $a > 0$ nên loại A, C
Đồ thị hàm số có điểm cực tiểu là $\left( {0; - 3} \right).$
Do hàm số chỉ có một điểm cực trị nên $y' = 0$ phải có duy nhất một nghiệm ${x_0}$ và $y\left( {{x_0}} \right) = - 3.$
Kiểm tra ta chỉ thấy đáp án D là phù hợp.
Ngoài ra, đáp án B bị loại vì phương trình $y'=0$ ở đáp án B có $3$ nghiệm phân biệt.
Hướng dẫn giải:
Quan sát đồ thị hàm số và nhận xét dáng điệu đồ thị, điểm cực đại, cực tiểu, đối chiếu các đáp án đã cho.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai?
Cho hàm số $y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx.$ Tìm $m$ để đồ thị hàm số có hai điểm cực trị là $A, B$ sao cho đường thẳng $AB$ vuông góc với $d:\,x - y - 9 = 0$
Nếu $\log_a b{\rm{ }} = {\rm{ }}p$ thì $\log_a{a^2}{b^4}$ bằng:
Cho $n \in Z, n>0$, với điều kiện nào của $a$ thì đẳng thức sau xảy ra: ${a^{ - n}} = \dfrac{1}{{{a^n}}}$?
Với điều kiện các logarit đều có nghĩa, chọn mệnh đề đúng:
Cho các phát biểu sau:
(I). Nếu \(C = \sqrt {AB} \) thì \(2\ln C = \ln A + \ln B\) với $A, B$ là các biểu thức luôn nhận giá trị dương.
(II). \(\left( {a - 1} \right){\log _a}x \ge 0 \Leftrightarrow x \ge 1\) với \(a > 0,a \ne 1\)
(III). \({m^{{{\log }_a}m}} = {n^{{{\log }_a}n}},\) với \(m,n > 0\) và \(a > 0,a \ne 1\)
(IV).\(\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = - \infty \)
Số phát biểu đúng là
Biết đồ thị các hàm số $y = {x^3} + \dfrac{5}{4}x - 2$ và $y = {x^2} + x - 2$ tiếp xúc nhau tại điểm $M({x_0}\,;\,{y_0})$. Tìm ${x_0}.$
Chọn kết luận đúng: Đồ thị hàm số bậc bốn trùng phương
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?
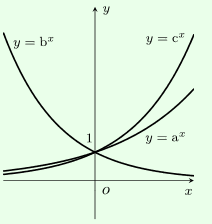
Cho các đồ thị hàm số \(y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c \ne 1} \right)\), chọn khẳng định đúng:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, \(AB = 4,SA = SB = SC = 12\). Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \(\dfrac{{BF}}{{BS}} = \dfrac{2}{3}\). Thể tích khối tứ diện \(MNEF\) bằng