Biết rằng \(F\left( x \right) = {e^{2x}}\left( {a\cos 3x + b\sin 3x} \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = {e^{2x}}\cos 3x\), trong đó a, b, c là các hằng số. Giá trị của tổng \(S = a + b\) thỏa mãn:

Tích phân \(\int\limits_{0}^{1}{{{e}^{-x}}}\,\text{d}x\) bằng

Cho \(A = \int {{x^5}\sqrt {1 + {x^2}} dx = a} {t^7} + b{t^5} + c{t^3} + C\) , với \(t = \sqrt {1 + {x^2}} \). Tính \(A = a - b - c\)

Biết $F\left( x \right) = \left( {ax + b} \right).{e^x}$ là nguyên hàm của hàm số $y = \left( {2x + 3} \right).{e^x}$. Khi đó $b - a$ là

Cho $I = \int\limits_0^1 {\left( {2x - {m^2}} \right)dx} $. Có bao nhiêu giá trị nguyên dương m để $I + 3 \ge 0$?

Nếu đặt $\left\{ \begin{array}{l}u = \ln \left( {x + 2} \right)\\{\rm{d}}v = x\,{\rm{d}}x\end{array} \right.$ thì tích phân $I = \int\limits_0^1 {x.\ln \left( {x + 2} \right){\rm{d}}x} $ trở thành

Tính \(I = \int {\cos \sqrt x dx} \) ta được:

Cho hàm số $f\left( x \right)$ liên tục trên $R$  và $\int\limits_{ - 2}^4 {f\left( x \right)} dx{\rm{ = 2}}$ . Mệnh đề nào sau đây là sai?

Cho \(I=\int{{{x}^{3}}\sqrt{{{x}^{2}}+5}dx}\), đặt \(u=\sqrt{{{x}^{2}}+5}\) khi đó viết \(I\) theo \(u\) và \(du\) ta được:

Tìm nguyên hàm của hàm số $f\left( x \right) = {x^2}ln\left( {3x} \right)$

Tích phân \(\int\limits_{1}^{2}{{{(x+3)}^{2}}dx}\) bằng

Cho \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\). Với \(C \ne 0\) là một hằng số bất kì, hàm nào sau đây cũng là một nguyên hàm của \(f\left( x \right)\)?

Tập nghiệm của bất phương trình\({\log _2}\left( {x\sqrt {{x^2} + 2}  + 4 - {x^2}} \right) + 2x + \sqrt {{x^2} + 2}  \le 1\) là \(\left( { - \sqrt a ; - \sqrt b } \right]\). Khi đó \(ab\) bằng

Thầy C gửi \(5\) triệu đồng vào ngân hàng với lãi suất \(0,7\% \)/tháng. Chưa đầy một năm thì lãi suất tăng lên thành \(1,15\% \)/tháng. Tiếp theo, sáu tháng sau lãi suất chỉ còn \(0,9\% \)/tháng. Thầy C tiếp tục gửi thêm một số tháng nữa rồi rút cả vỗn lẫn lãi được 5787710,707 đồng. Hỏi thầy C đã gửi tổng thời gian bao nhiêu tháng?

Cho hai số thực dương $x, y$ thỏa mãn \({2^x} + {2^y} = 4\). Tìm giá trị lớn nhất \({P_{\max }}\) của biểu thức\(P = (2{x^2} + y)(2{y^2} + x) + 9xy\).

Biết \(a,\,\,b\) là các số thực sao cho \({x^3} + {y^3} = a{.10^{3z}} + b{.10^{2z}}\), đồng thời \(x,\,\,y,\,\,z\) là các số thực dương thỏa mãn \(\log \left( {x + y} \right) = z\) và \(\log \left( {{x^2} + {y^2}} \right) = z + 1\). Giá trị của \(\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}\) thuộc khoảng:

Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0\) nghiệm đúng với mọi giá trị \(x \in \left[ {1;64} \right]\).

Cho hàm số $f\left( x \right) = \dfrac{{{3^x}}}{{{7^{{x^2} - 4}}}}$. Hỏi khẳng định nào sau đây là sai?

Tích các nghiệm của phương trình \({\left( {3 + \sqrt 5 } \right)^x} + {\left( {3 - \sqrt 5 } \right)^x} = {3.2^x}\)  là:

Cho hàm số $y = x.{e^{ - x}}$. Chọn kết luận đúng:

Cho $a,{\rm{ }}b,{\rm{ }}c$ là các số thực dương thỏa mãn ${a^2} = bc.$ Tính $S = 2\ln a - \ln b - \ln c$.

Đặt ${\log _2}3 = a;{\log _2}5 = b$. Hãy biểu diễn $P = {\log _3}240$ theo $a$ và $b$.

Nếu ${\left( {a - 2} \right)^{ - \dfrac{1}{4}}} \le {\left( {a - 2} \right)^{ - \dfrac{1}{3}}}$ thì khẳng định đúng là:

Biết rằng phương trình $2\log \left( {x + 2} \right) + \log 4 = \log x + 4\log 3$ có hai nghiệm phân biệt \({x_1},{\rm{ }}{x_2}\,\,\left( {{x_1} < {x_2}} \right)\). Tính \(P = \dfrac{{{x_1}}}{{{x_2}}}.\)

Hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) xác định trên:

Gọi $(C)$ là đồ thị hàm số \(y = \log x\). Tìm khẳng định đúng? 

Cho các số \(a,\ b,\ c\) và \(a,\ c\ne 1\). Khẳng định nào sau đây đúng?

Bất phương trình \({\left( {\sqrt 2 } \right)^{{x^2} - 2x}} \le {\left( {\sqrt 2 } \right)^3}\)  có tập nghiệm là:

Tìm $x$ để biểu thức \({\left( {{x^2} + x + 1} \right)^{ - \dfrac{{2\pi }}{3}}}\) có nghĩa:

Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng

Đề thi THPT QG - 2021 - mã 103

Trên khoảng \(\left( {0; + \infty } \right)\), đạo hàm của hàm số \(y = {x^{\frac{4}{3}}}\) là:

Một người gửi tiết kiệm vào ngân hàng số tiền $A$ đồng, lãi suất mỗi tháng là $r$, gửi theo hình thức lãi kép không kì hạn. Công thức tính số tiền cả vốn lẫn lãi mà người đó nhận được sau $N$ kì hạn là:

Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?

Một người gửi vào ngân hàng số tiền $A$ đồng, lãi suất $r\% $ mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kì hạn $3$ tháng. Công thức tính số tiền cả vốn lẫn lãi mà người đó có sau $2$ năm là:

Tính tổng \(T\) tất cả các nghiệm của phương trình \({\left( {x - 3} \right)^{2{x^2} - 5x}} = 1\).

Cho \({\left( {\sqrt 5  - 1} \right)^m} < {\left( {\sqrt 5  - 1} \right)^n}\). Khẳng định nào dưới đây đúng?

Kết luận nào đúng về số thực \(a\) nếu \({(2a + 1)^{ - 3}} > {(2a + 1)^{ - 1}}\)

Tìm tất cả các giá trị thực của tham số m để phương trình \({\log _2}\left( {{5^x} - 1} \right).{\log _4}\left( {{{2.5}^x} - 2} \right) = m\) có nghiệm \(x \ge 1\) ?

Cho \(x;y\) là hai số thực dương thỏa  mãn \(x \ne y\) và \({\left( {{2^x} + \dfrac{1}{{{2^x}}}} \right)^y} < {\left( {{2^y} + \dfrac{1}{{{2^y}}}} \right)^x}.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\).

Thầy C gửi \(5\) triệu đồng vào ngân hàng với lãi suất \(0,7\% \)/tháng. Chưa đầy một năm thì lãi suất tăng lên thành \(1,15\% \)/tháng. Tiếp theo, sáu tháng sau lãi suất chỉ còn \(0,9\% \)/tháng. Thầy C tiếp tục gửi thêm một số tháng nữa rồi rút cả vỗn lẫn lãi được 5787710,707 đồng. Hỏi thầy C đã gửi tổng thời gian bao nhiêu tháng?

Tìm tập nghiệm $S$ của bất phương trình ${\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}(x) > {\log _2}({x^2} - x) - 1$

Xét hệ phương trình  \(\left\{ \begin{array}{l}{2^x} - {2^y} = y - x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} + xy + {y^2} = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)có nghiệm \(\left( {x;y} \right)\). Khi đó phát biểu nào sau đây đúng:

Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).

Tìm số các giá trị nguyên không dương của tham số \(m\) để hàm số \(y = \dfrac{{m\ln x - 2}}{{\ln x + m - 3}}\) đồng biến trên \(\left( {{e^2}; + \infty } \right)\) là

Gọi \(m,M\) lần lượt là GTNN, GTLN của hàm số \(y = {e^{2 - 3x}}\) trên đoạn \(\left[ {0;2} \right]\). Mệnh đề nào sau đây đúng?

Một người mua xe máy với giá 45 triệu đồng. Biết rằng giá trị khấu hao tài sản xe giảm 60% mỗi năm. Hỏi sau bao nhiêu năm thì giá trị xe chỉ còn 5 triệu đồng?

Cho hàm số \(f\left( x \right) = {\left( {{x^{1 + \dfrac{1}{{2{{\log }_4}x}}}} + {8^{\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} + 1} \right)^{\dfrac{1}{2}}} - 1\)  với \(0 < x \ne 1\). Tính giá trị biểu thức \(P = f\left( {f\left( {2018} \right)} \right)\).

Với \(a,\,b\) là các số thực dương bất kì, \({\log _2}\dfrac{a}{{{b^2}}}\) bằng:

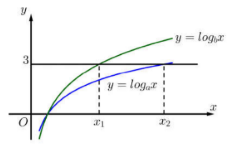
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:

Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:

Tìm tập nghiệm $S$ của bất phương trình ${2^{x - 1}} > {\left( {\dfrac{1}{{16}}} \right)^{\frac{1}{x}}}$ .